Las cotas de complejidad nos ayudan a clasificar los algoritmos de acuerdo a su tiempo de ejecución. Si tenemos un algoritmo que para una entrada n tarda f(n) en ejecutarse, lo que nos interesa es encontrar una cota que crezca de manera similar a f(n).



Dada una función f, queremos estudiar aquellas funciones g que a lo sumo crezcan tan deprisa como f. Lo que buscamos es que para una función g(n), encontrar una función asintótica que cumpla:

En términos más sencillos, si tenemos una función O(n²), quiere decir que el tiempo de ejecución f(n) nunca será mayor a cn². Como estamos acotando por la parte superior, si un algoritmo cumple O(n²), también cumple O(n³) (o cualquier otra función de orden mayor), ya que si f(n) ≤ cn² con mayor razón f(n) ≤ cn³.

Normalmente estamos interesados en la función de menor crecimiento que satisfaga la cota y es común asumir que, en efecto, es la menor que cumple. Nosotros lo haremos a lo largo de este libro, a menos que se especifique lo contrario.

La notación O se utiliza la mayoría de las veces para acotar el peor caso de un algoritmo, ya que implica que cualquier otra entrada correrá en un tiempo menor o igual que el especificado por la función.

Algo interesante de esta notación es que en algoritmos iterativos se puede calcular fácilmente contando el mayor número de ciclos anidados de la implementación (aunque no garantiza que sea la menor función).

Existe una notación alterna muy similar, que es la notación o (omicrón minúscula). La diferencia es que debe cumplir que 0 ≤ f(n) < cg(n). Es decir, para un algoritmo con tiempo de ejecución n² se cumple O(n²) pero no o(n²). Esta notación indica que cuando las dos funciones tienden a infinito, f(n) se vuelve insignificante en comparación a g(n). Es muy inusual que se use esta notación.

Dada una función f, queremos estudiar aquellas funciones g que a los sumo crecen tan lentamente como f. Esta cota define que, para una función g(n), tenemos una función asintótica la cual cumple:

Esto significa que para valores más grandes que n₀, los resultados de f(n) no pueden ser menores a Ω(n).

Como esta notación especifica un límite inferior, es común que se utilice para acotar el caso de mejor tiempo de ejecución, ya que cualquier otro caso tiene que ser forzosamente mayor a éste.

Al igual que con la cota superior, la cota inferior que es más útil es aquella que se aproxima en mayor grado a f sin sobrepasarla, y estará implícito dentro del libro. También de manera análoga a O, existe una notación similar a Ω que es ω (omega minúscula). En esta cota se cumple que 0 ≤ cg(n) < f(n), y tampoco es utiliza comúnmente.



Dada una función f, buscamos las funciones g que tienen un crecimiento igual a f:

Lo que se quiere decir con esto, es que a partir de cierto número n₀ cualquier valor de f(n) se va a encontrar “empacado” entre c₁g(n) y c₂g(n). La cota ajustada está cumpliendo al mismo tiempo que la función g crezca tan lentamente y tan deprisa como f.

Esta notación se acostumbra utilizarla para acotar el tiempo medio de ejecución de un algoritmo.

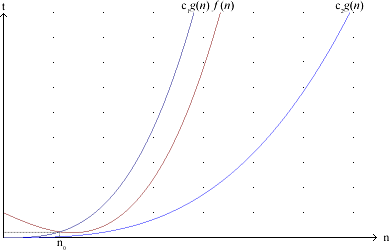Figura 2.1: Representación gráfica de la notación Θ

Cualquiera de las tres cotas se puede utilizar con cualquiera de los tres tiempos de ejecución, pero es conveniente utilizarlos de la forma que se mencionó.

La cota más utilizada es O, seguida por Θ, por las mismas razones de los casos de tiempo de ejecución, además de que resulta más sencillo calcular la primera que la segunda.

Como el caracter Θ no pertenece a los caracteres ASCII, es común que se llegue a cambiar, ya sea por conveniencia o por error, por el caracter O. Dado que si tenemos que f(n) 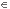Θ(g(n)) → f(n) 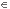O(g(n)), no hay mucho problema excepto que se pierde precisión. Esto es considerando que con O y Θ estemos hablando de un mismo caso (posiblemente el promedio), pero si los estamos utilizando una para el peor caso y otra para el promedio, entonces lo anterior no se cumple. Por ejemplo: si tenemos que para un algoritmo su tiempo promedio es Θ(nlgn) y el peor es O(n²), podemos decir que el tiempo para el caso promedio es O(nlgn) pero no podemos decir lo mismo del peor caso.