La forma más sencilla para implementar la multiplicación es mediante la repetición de sumas. Si necesitamos el resultado de m×n, lo podemos obtener sumando n veces m, ó m veces n. Esto podría resultar práctico para números pequeños, pero como estamos tratando con números grandes este procedimiento es demasiado lento.
El siguiente enfoque que podríamos tomar es el de implementar la multiplicación tal como nos las enseñaron en la escuela. El primer problema que se nos presentaría es el tamaño de los bloques. Si tenemos bloques con hasta nueve dígitos, el resultado de multiplicar dos de ellos puede llegar al doble de dígitos (que serían 18). Para poder seguir realizando las operaciones con el mismo tipo de variable tendríamos que ajustar la base a sólo la mitad, por lo que de 9 dígitos pasaríamos a 4. Esto influye significativamente en la velocidad de los algoritmos, ya que ahora tendríamos que hacer más del doble de operaciones. El otro problema inmediato con el que nos enfrentaríamos es que la multiplicación es una operación costosa en cuestión de tiempo para el procesador.
Ambos problemas los podemos solucionar trabajando con el mismo algoritmo pero en base dos. A esta forma de multiplicar se le conoce como la multiplicación del campesino ruso ya que todavía se utiliza en algunos sectores de Rusia, aunque en realidad fue descubierto por lo egipcios antiguos. Lo interesante de utilizar este método es que en ningún momento necesitamos multiplicar, sino que funciona con sumas, y multiplicaciones y divisiones por 2 las que cambiaremos por desplazamientos.
Para ver como funciona este método, primero vamos utilizar un ejemplo en base 10 para luego cambiarlo a base 2. Supongamos que tenemos que multiplicar 36×217. Lo que normalmente hacemos es lo siguiente:
| 36 |
| × 217 |
| 252 |
| 36 |
| 72 |
| 7812 |
Lo que estamos haciendo es descomponer la multiplicación de la siguiente forma: 36×217= 36×7 + (36×1)×10 + (36×2)×100. El algoritmo sería el siguiente: tomamos el primer dígito del multiplicador y realizamos la operación, seguimos con el segundo dígito y hacemos lo mismo pero el resultado lo movemos un lugar a la izquierda (lo desplazamos), nos vamos al último dígito, realizamos la misma operación y el resultado lo movemos dos lugares. Podemos seguir con este proceso en caso de que el número contenga más dígitos. Al final sólo necesitamos sumar todos los resultados para obtener toda la multiplicación.
Haciendo de manera similar en base 2, lo que efectuamos es descomponer la multiplicación de la siguiente manera: 36×217 = 36×1 + (36×0)×2 + (36×0)×4 + (36×1)×8 + (36×1)×16 + (36×0)×32 + (36×1)×64 + (36×1)×128. Como podemos apreciar, dentro de los paréntesis sólo multiplicamos ya sea por uno o por cero, por lo que en realidad no necesitamos efectuar la operación. En caso de multiplicar por uno el resultado es el mismo, y en caso multiplicar por cero el resultado es cero.
Ahora lo que nos interesa es multiplicar por las potencias, lo cual podemos conseguir fácilmente. Empezando por 1, las siguientes potencias las obtenemos multiplicando por dos la potencia anterior, pero está operación la podemos cambiar por un corrimiento a la izquierda.
El único inconveniente sería cambiar el multiplicador a base dos. Esto no es tan complicado como pudiera parecer a primera vista. Como vimos en el capítulo 5.4, podemos pasar un número a base 2 dividiéndolo continuamente entre 2 y tomando los residuos en orden inverso a como los calculamos. La división la podemos reemplazar con un desplazamiento, además de que para conocer el residuo basta con saber si el número es par o impar.
El tiempo de ejecución de este algoritmo es de O(n2), donde n es la cantidad de bits del número. Esto sin importar en que base trabajemos, ya que al efectuar la multiplicación necesitamos recorrer todos los dígitos de los dos números. La ventaja de la base 2 es que el costo de las operaciones es mucho menor.
Existen algoritmos que mejoran significativamente la complejidad de multiplicar dos números grandes. Aunque no los vamos a revisar a fondo en este estudio, los mencionaremos rápidamente por si el lector está interesado en tener un algoritmo más eficiente.
El primero de ellos es la multiplicación de Karatsuba, que utiliza una estrategia “divide y vencerás”, y con el cual se obtiene un tiempo de ejecución de O(n1.58). Este método se basa en que si tenemos dos números x e y, los podemos descomponer de la siguiente forma x = x1b + x0 e y = y1b + y0. Habitualmente, lo que hacemos al multiplicar es x×y = (x1b + x0) × (y1b + y0) = x1y1b2 + (x1y0 + x0y1)b + x0y0. No obstante, esto lo podemos reacomodar de la siguiente forma x×y = (b2 + b)x1y1 -b(x1 – x0)(y1 – y0) + (b + 1)x0y0. Con esto, logramos efectuar sólo tres multiplicaciones mientras que si multiplicáramos de la forma convencional tendríamos que hacer cuatro. Para hacer las operaciones correspondientes podemos utilizar los algoritmos que ya tenemos.
Podemos utilizar la misma idea y dividir al número en más partes. Si efectuamos particiones de tamaño tres, conseguimos un algoritmo conocido como Toom-Cook 3, que tiene complejidad O(n1.46). Hacer mas particiones resulta en una disminución en la complejidad del algoritmo pero al mismo tiempo se va incrementando el tiempo en el que se realiza cada operación, por lo que para efectos prácticos la ventaja de uso sólo se aprecia en números significativamente grandes. Por último, para números mucho muy grandes podemos utilizar una transformada rápida de Fourier.
Problema ejemplo
ab -ba
Problema
Para dados dos números naturales a y b, encontrar ab -ba.Entrada
El archivo de entrada contiene los números a y b (1 ≤ a, b ≤ 100).Salida
Escribe la respuesta en el archivo de salida.Solución: Para obtener el resultado vamos a efectuar las operaciones que nos piden. Para agilizar la potenciación, podemos emplear el algoritmo de la sección 5.5.
Código
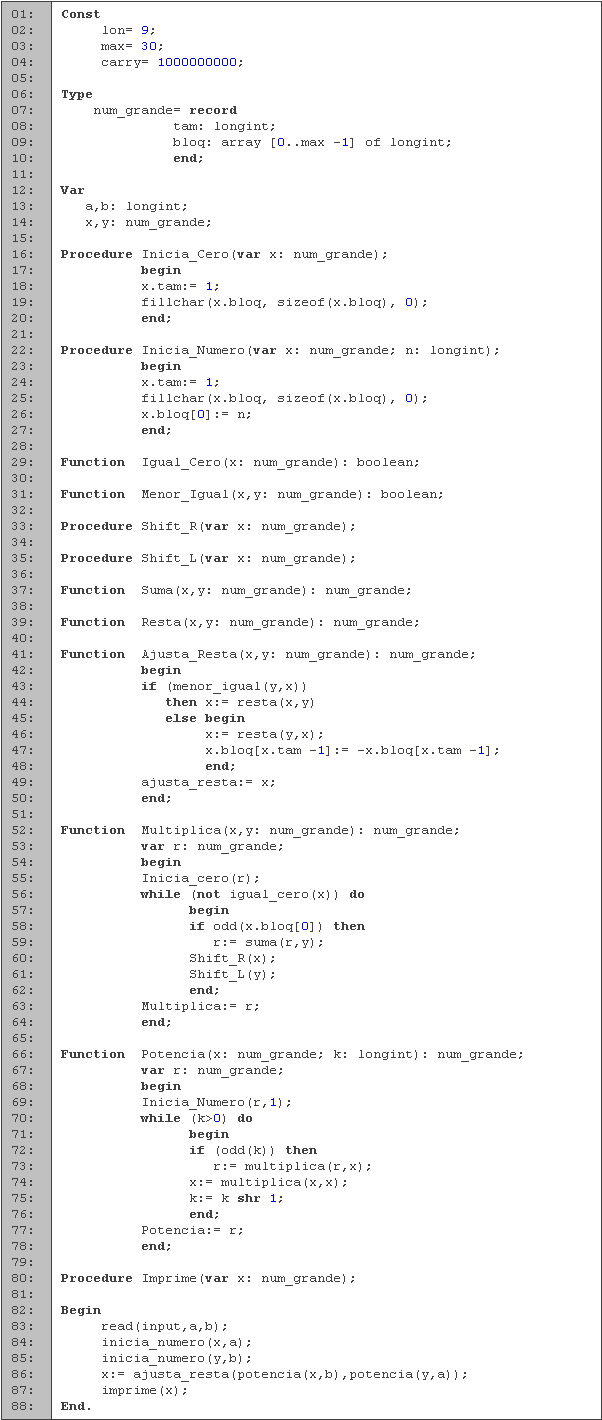
Empezamos por definir en las primeras cuatro líneas las constantes que vamos a ocupar para el manejo de números grandes. En seguida definimos la estructura que va a contener los números grandes (líneas 6 a 10). El número máximo que en teoría vamos a utilizar es menor a 100100 que contiene 201 dígitos, por lo que necesitaríamos
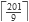 = 23 bloques. Sin embargo, debemos tener en cuenta que dentro de algunas operaciones los valores intermedios pueden exceder esta cifra por lo que es conveniente sobredimensionar un poco.
= 23 bloques. Sin embargo, debemos tener en cuenta que dentro de algunas operaciones los valores intermedios pueden exceder esta cifra por lo que es conveniente sobredimensionar un poco.Seguimos con la declaración de variables de la línea 12 a la 14. En las variables a y b leemos la entrada. Las variables x e y las utilizamos para guardar los números grandes.
Tenemos dos procedimientos de inicialización de números grandes: inicia_cero (líneas 16 a 20) que sirve para inicializar un número a cero, e inicia_numero (líneas 22 a 27) que asigna un número entero a un número grande. Lo que hacemos en ambos casos es primero igualar el tamaño dinámico a 1 y limpiar todos los bloques del número. Con esto el primer procedimiento está completo, mientras que en el segundo sólo necesitamos igualar el primer bloque al entero para terminar.
La implementación de las funciones igual_cero, menor_igual, shift_l, shift_r, suma, resta e imprime (líneas 29 a 39, y línea 80) son las mismas que vimos en secciones anteriores.
Sabemos que nuestra implementación de la substracción sólo funciona en el rango de los naturales, pero en el problema se presentan casos en los que el resultado va a ser negativo. Para poder manejar esto, creamos la función ajusta_resta que se halla entre las líneas 41 y 50. Sabemos que después de la resta no vamos a realizar otras operaciones, y que si invertimos el orden de la resta (el minuendo y el sustraendo) lo único que cambia es el signo, así que si ocurre que el minuendo es menor al sustraendo los cambiamos de orden e incluimos el signo en el bloque más significativo.
La función multiplica da como resultado la multiplicación de los dos parámetros. Como ya se explicó, el procedimiento consiste en ir desplazando a la derecha el multiplicador, a la izquierda el multiplicando e ir guardando la suma de los dos cada vez que el primero sea impar.
La parte principal del código la encontramos de las líneas 82 a 88. Aquí no necesitamos más que leer la entrada, realizar las operaciones y mandar a imprimir el resultado.
Caso ejemplo
| Entrada: | 8 3 |
| Desarrollo: | 83 = 81×82 = 512 38 = ((32)2)2 = 6561 512 –6561 = -6049 |
| Salida: | -6049 |
Nota: El desarrollo es demasiado grande para poderlo incluir completamente. Dado que la parte más importante del algoritmo es la multiplicación, a continuación veremos la última que se efectúa.
| Desarrollo: | (34)2 = 81×81 81 81, 81 impar, r= 81 40 162, 40 par, r= 81 20 324, 20 par, r= 81 10 648, 10 par, r= 81 5 1296, 5 impar, r= 81 + 1296= 1377 2 2592, 2 par, r= 1377 1 5184, 1 impar, r= 1377 + 5184= 6561 |
Código en C
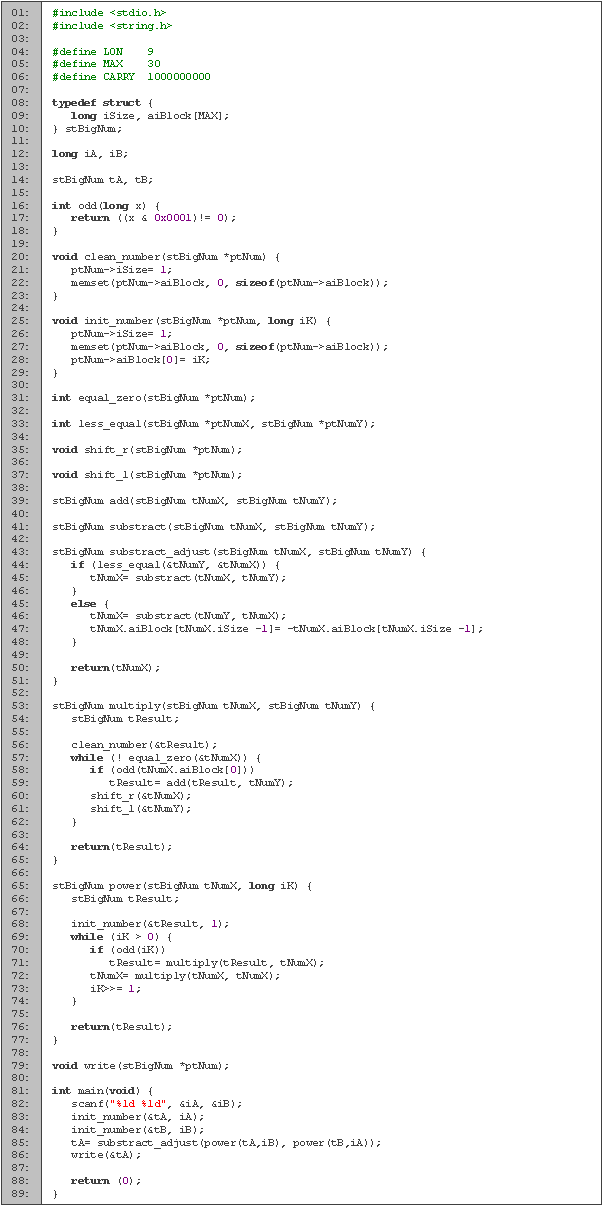
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 16-Feb-2006 | 0.045 | 0.000 | - | - | 145 |
| C | 16-Feb-2006 | 0.067 | 358 | |||
Otros problemas
Valladollid:
Ural:
Project Euler:
Sphere:
 Substracción
Substracción
