En el problema de la mochila buscamos la forma en que podemos guardar objetos dentro de una mochila, con las restricciones de que necesitamos tener en la mochila los objetos de mayor costo (valor) posible y que el peso total no debe sobrepasar a un límite dado. Contamos con el costo y el peso de cada objeto, y disponemos de una cantidad ilimitada de ellos.
Este problema de optimización es NP-difícil, y puede ser replanteado como problema de decisión NP-completo de la siguiente forma: “podemos tener un costo de por lo menos c sin exceder el peso w?”.
Existe una versión más simple del problema, donde en lugar de tener una infinidad de elementos, sólo tenemos uno de cada tipo por lo que la decisión se reduce a si tomarlo o no. A este problema se le conoce como la mochila cero-uno.
Para resolver el problema de la mochila cero-uno, podemos considerar una función C, la que obtiene el máximo valor que se puede obtener teniendo un peso menor o igual j y utilizando hasta i objetos. Esta función la podemos obtener considerando los siguientes casos:
- Si no tenemos objetos, el valor máximo es cero. C(0, j) = 0.
- Si a la mochila no le caben más objetos (se llegó al peso máximo), el valor máximo que podemos agregar es cero. C(i, 0) = 0.
- Escogemos el de mayor beneficio entre tomar o no el objeto i. Si tomamos el objeto i, el peso de los demás objetos tiene que ser menor o igual a j -wi (el cual no debe ser negativo). C(i, j) = max(C(i-1,j), C(i-1, j-wi)+ci).
Problema ejemplo
SuperVenta
Problema
Hay promoción de SuperVenta en el SuperHiperMercado. Cada persona puede llevar solamente una unidad de cada mercancía (por ejemplo, una televisión o una zanahoria), pero a un precio muy bajo. Vamos a ir en familia al SuperHiperMercado. Cada persona tratará de comprar tanta mercancía como pueda en la SuperVenta. Hemos obtenido una lista con el precio y el peso de cada mercancía. También conocemos cual es el peso máximo que puede cargar cada persona. ¿Cuál es valor máximo de mercancías que se pueden comprar en la SuperVenta?Entrada
La entrada consiste en t casos. La cantidad de casos (1 ≤ t ≤ 1000) está dado en la primera línea de la entrada.Cada caso comienza con una línea que contiene a un solo entero n que indica la cantidad de objetos (1 ≤ n ≤ 1000). Después le siguen n líneas, cada una con dos enteros: p y w. El primer entero (1 ≤ p ≤ 100) corresponde al precio del objeto. El segundo entero (1 ≤ w ≤ 30) corresponde al peso del objeto. La siguiente línea contiene un entero (1 ≤ g ≤ 100) que representa la cantidad de personas en la familia. Las g líneas que le siguen contienen el peso máximo (1 ≤ mw ≤ 30) que el i-ésimo miembro de la familia puede cargar (1 ≤ i ≤ g).
Salida
Para cada caso prueba, tu programa debe calcular un entero. Imprime el valor máximo de las mercancías que puedes comprar con esa familia.
Solución: Para cada caso, leemos los pesos y los costos, y utilizamos los casos anteriores para obtener los valores máximos de la mochila. Algo importante es no calcular la mochila para cada persona en g, sino sólo calcular para el valor mayor de mw ya que los demás valores son subproblemas de éste y los podemos obtener al mismo tiempo.
Código
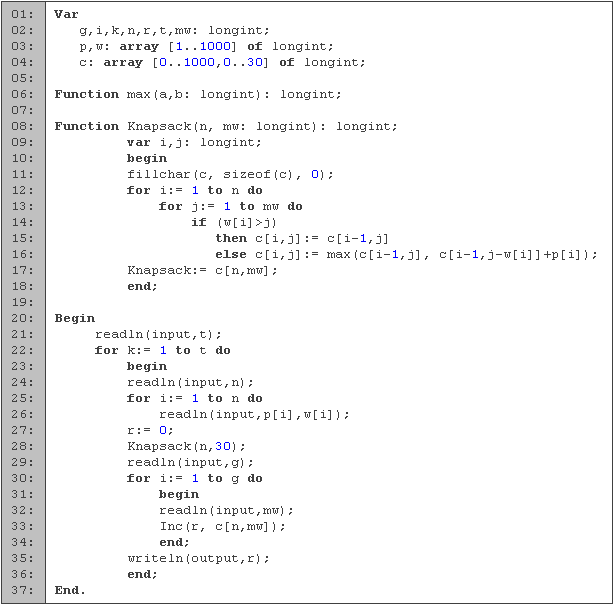
En las primeras cuatros líneas declaramos las variables que vamos a utilizar. Para los ciclos utilizamos i y k, las variables g, n, t, mw, p, w, las utilizamos de acuerdo a las especificaciones del problema, sólo que las dos últimas las hacemos arreglos. En la matriz c guardamos los resultados intermedios de la mochila, y el resultado total lo guardamos en r.
La función max (línea 6) nos devuelve el menor de los dos parámetros. La implementación es la misma que en problemas anteriores.
En la función knapsack (líneas 8 a 18) calculamos el valor máximo que podemos guardar en la mochila. Las variables i y j, las utilizamos para los ciclos. Comenzamos limpiando la matriz c (línea 11). Para cada objeto de la mochila (línea 12), vamos calculando el precio máximo que podemos obtener con un peso máximo de j (líneas 13 a 16). Al final regresamos el precio máximo que podemos obtener utilizando todos los objetos (línea 17).
Caso ejemplo
| Entrada: |
2 5 52 1 79 6 13 12 76 11 60 4 3 7 11 4 3 65 2 50 10 59 8 4 12 5 2 5 |
| Desarrollo: |
C[] w 52 52 52 52 52 52 52 52 52 52 52 52 52 52 52 52 52 79 131 131 131 131 131 131 n 52 52 52 52 52 79 131 131 131 131 131 131 52 52 52 52 52 79 131 131 131 131 131 131 52 52 52 60 112 112 131 131 131 139 191 191 c[5,7] = 131; r= 131; c[5,11]= 191; r= 322; c[5,4] = 60; r= 382; C[] w 0 65 65 65 65 65 65 65 65 65 65 65 n 0 65 65 65 65 65 65 65 65 65 65 115 0 65 65 65 65 65 65 65 65 124 124 124 c[5,12]= 124; r= 124; c[5,5] = 65; r= 189; c[5,2] = 65; r= 254; c[5,5] = 65; r= 319; |
| Salida: |
382 319 |
Posibles Cambios
El tiempo de ejecución de este algoritmo es de O(nW), donde n es la cantidad de objetos y W el peso máximo. Esta solución es pseudo-polinomial, ya que, aunque parece polinomial, en realidad W no está en función del tamaño de la entrada.
Podemos mejorar algunos aspectos del algoritmo. Cuando el peso máximo es grande, es mejor utilizar una estrategia “arriba hacia abajo” para evitar cálculos innecesarios.
También es posible reducir el tamaño de matriz observando que sólo estamos utilizando el renglón actual y el anterior, y que las casillas que estamos modificando en el renglón actual con respecto al anterior son van del peso actual al peso máximo. Con esto podemos reducir fácilmente la matriz a dos renglones, y con algunos cambios, a un renglón.
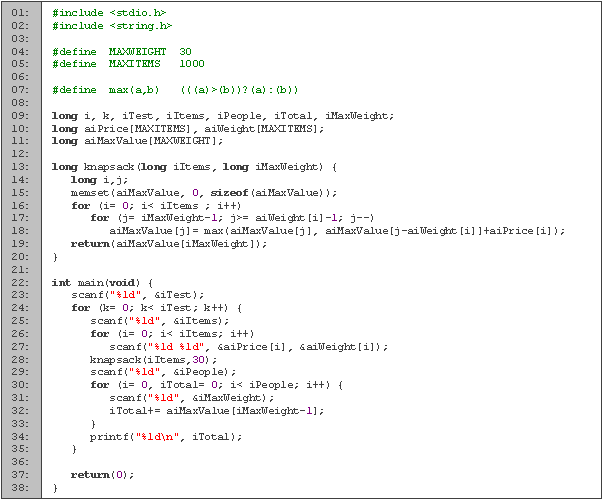
Código en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 5-Jun-2006 | 0.119 | 0.037 | 0.219 | 14.710 | 448 |
| C | 10-Jun-2006 | 0.105 | 396 | |||
Otros problemas
Valladolid:
 Transformación de cadenas
Transformación de cadenas
