Teniendo una sucesión de matrices que van a ser multiplicadas, queremos escoger el modo óptimo de realizar las operaciones para minimizar la cantidad de multiplicaciones escalares. Por ejemplo, teniendo las matrices A1, A2 y A3, la multiplicación viene dada por A1A2A3, que podemos obtener como (A1A2)A3 o A1(A2A3).
Supongamos que la primera matriz es de 10×20, la segunda de 20×30 y la tercera de 30×40. Utilizando (A1A2)A3 la cantidad de operaciones que realizamos es (10×20×30) + (10×30×40) = 18000, mientras que con A1(A2A3) ocupamos (20×30×40) + (10×20×40) = 32000 operaciones. Podemos apreciar como la primera multiplicación es significativamente más eficiente que la segunda.
Una opción es realizar todas las posibles formas para poner paréntesis en la multiplicación, pero esto requeriría un tiempo exponencial (O(2n)). Para resolverlo en tiempo polinomial, vamos a aprovechar la subestructura óptima de este problema.
Supongamos que queremos optimizar el número de operaciones en la multiplicación AiAi+1...Aj, a la cual representaremos como Ai..j. Para hacerlo, podemos partir a la sucesión en dos de tal forma que al sumar las partes tengamos un resultado óptimo, o lo que es lo mismo, debemos encontrar una k tal que la suma de operaciones de Ai..k, Ak..j y al juntarlas sea mínima.
Con esto reducimos la complejidad a un tiempo polinomial de O(n3), sacrificando a cambio espacio en memoria para guardar todos los valores de Ai..j. También existe un algoritmo que logra un tiempo de O(nlgn) convirtiendo el problema a un equivalente geométrico, donde se busca encontrar todas las formas en que un polígono convexo se puede cortar en triángulos que no se intersecten.
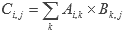
La cantidad de columnas en el arreglo A debe ser igual a la cantidad de filas del arreglo B. Como notación, diremos que filas(A) y columnas(A) son la cantidad de filas y columnas, respectivamente, del arreglo A. La cantidad de multiplicaciones individuales requeridas para calcular el arreglo C (que tendrá la misma cantidad de filas que A y de columnas que B) es filas(A) × columnas(B) × columnas(A). Por ejemplo, si A es un arreglo de 10×20 y B uno de 20×15, tomaría 10×15×20, o 3000 multiplicaciones calcular el arreglo C.
Para realizar multiplicaciones de más de dos arreglos tenemos varias opciones de como proceder. Por ejemplo, si X, Y y Z son arreglos, entonces para calcular X × Y × Z podríamos utilizar (X × Y) × Z o X × (Y × Z). Supongamos que X es un arreglo de 5×10, Y uno de 10×20 y Z uno de 20×35. Veamos la cantidad de productos utilizados en las dos series distintas:
(X × Y) × Z
· 5×20×10 = 1000 multiplicaciones para encontrar el producto (X × Y), un arreglo de 5×20.
· Después se ocupan 5×35×20 = 3500 multiplicaciones para determinar el resultado final.
· Multiplicaciones totales: 4500.
X × (Y × Z)
· 10×35×20 = 7000 multiplicaciones para encontrar el producto (Y × Z), un arreglo de 10×35.
· Después se ocupan 5×35×10 = 1750 multiplicaciones para determinar el resultado final.
· Multiplicaciones totales: 8750.
Es claro que utilizando (X × Y) × Z requerimos menos multiplicaciones individuales.
Dado el tamaño de cada arreglo en una serie de arreglos a multiplicar, debes determinar la forma óptima de multiplicarlos. Por óptimo, en este problema, nos referimos a la cantidad mínima de multiplicaciones individuales requeridas.
Solución: Nos piden que encontremos la forma óptima de realizar las operaciones. Para hacerlo, vamos a utilizar la relación anterior, y cada vez que encontremos un valor óptimo, guardamos en una matriz auxiliar como la obtuvimos (cual valor de k utilizamos).

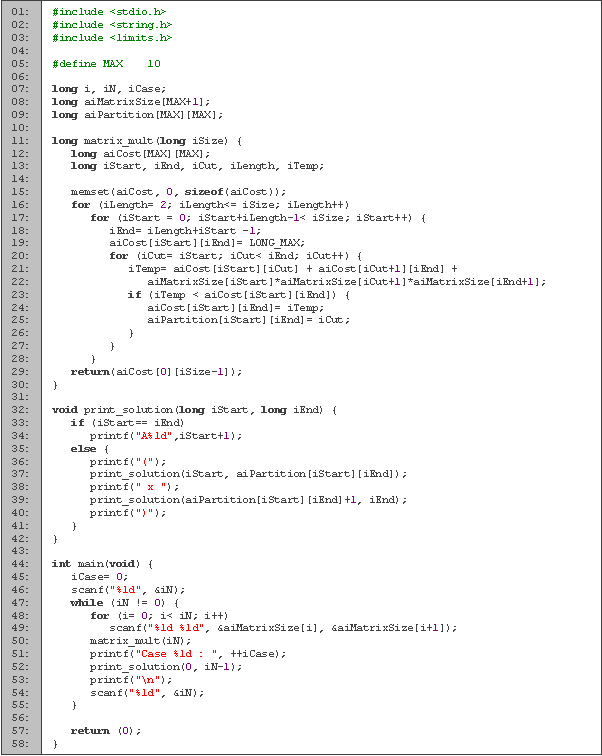
En las primeras cuatro líneas tenemos las variables que vamos a utilizar. En n leemos la cantidad de matrices a multiplicar, c para saber en cual caso estamos, i para los ciclos y el arreglo a para guardar el tamaño de las matrices. Como el número de renglones de una matriz es igual al número de columnas de la siguiente, guardamos este valor en la misma casilla en a.
Entre las líneas 6 y 27 tenemos la función matriz_mult, que es donde calculamos la cantidad mínima de operaciones. Los datos intermedios de los subproblemas los vamos a almacenar en m. Para obtener los valores de la matriz de “abajo hacia arriba”, tenemos que empezar con las sucesiones de menor tamaño. En el ciclo de la línea 11 vamos recorriendo las longitudes l que va a tomar la sucesión y en el ciclo de la línea 12 escogemos en cual matriz i vamos a comenzar. La longitud de una sucesión que empieza en i y termina en j es l = j-i + 1, despejando obtenemos el valor de j (línea 14). Como j tiene que ser a lo más n (j ≤ n), tenemos que l+i -1 ≤ n, y despejado i ≤ n-l + 1; con lo que obtenemos el valor máximo de nuestro segundo ciclo.
Una vez que tenemos los valores en los que empezamos y terminamos, escogemos todos los valores intermedios k que podemos tomar para optimizar la multiplicación. Antes de empezar, inicializamos el valor de las operaciones a infinito (línea 15). Si el valor de k que escogimos nos da una mejor partición (línea 19), guardamos el resultado y como lo obtuvimos (líneas 21 y 22). Terminamos devolviendo la cantidad mínima de operaciones que necesitamos (línea 26).
En seguida tenemos la función que imprime la forma en que se debe realizar la multiplicación (líneas 29 a 38). Como parámetros tenemos las variables i y j que nos indican el intervalo de matrices que vamos a multiplicar. Si el intervalo nada más incluye una matriz, la imprimimos (líneas 32 a 35); en caso contrario, utilizamos la multiplicación óptima de las matrices intermedias (líneas 36 y 37).
Al final, tenemos la parte principal del código (líneas 40 a 52). Leemos la cantidad de matrices (línea 42), y mientras sea distinto de cero, incrementamos el caso en el que vamos (línea 45), leemos el tamaño de las matrices (líneas 46 y 47), vemos la forma óptima de resolver la multiplicación (línea 48), imprimimos el resultado (línea 49) y leemos la cantidad de matrices del siguiente caso (línea 50).| Entrada: |
6 30 35 35 15 15 5 5 10 10 20 20 25 0 |
| Desarrollo: |
m[] 0 - - - - - 15750 0 - - - - 7875 2625 0 - - - 9375 4375 750 0 - - 11875 7125 2500 1000 0 - 15125 10500 5375 3500 5000 0 s[] 0 - - - - - 1 0 - - - - 1 2 0 - - - 3 3 3 0 - - 3 3 3 4 0 - 3 3 3 5 5 0 i j 1 6; '(' 1 3; '((' 1 1; '((A1' 2 3; '((A1 x (' 2 2; '((A1 x (A2' 3 3; '((A1 x (A2 x A3' 4 6; '((A1 x (A2 x A3)) x (' 4 5; '((A1 x (A2 x A3)) x ((' 4 4; '((A1 x (A2 x A3)) x ((A4' 5 5; '((A1 x (A2 x A3)) x ((A4 x A5' 6 6; '((A1 x (A2 x A3)) x ((A4 x A5) x A6' |
| Salida: | Case 1: ((A1 x (A2 x A3)) x ((A4 x A5) x A6)) |
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 27-Abr-2006 | 0.779 | 0.100 | 0.420 | 12.920 | 320 |
| C | 15-Jun-2006 | 0.371 | 396 | |||
Valladolid:
 Partición y composición de enteros
Partición y composición de enteros
