Queremos encontrar la distancia más corta entre dos vértices en un árbol. La forma más común en que se presenta este problema, es cuando queremos encontrar la ruta más corta para salir de un laberinto.
La característica especial en este problema es que la distancia entre vértice y vértice (el peso de la rama) es siempre uno (en caso de no serlo, ver sección 10.4). Si el vértice en el que comenzamos lo tomamos como la raíz del árbol, la distancia más corta a la salida es el nivel mínimo en el que encontramos un vértice de salida. Para encontrar el nivel mínimo, lo más conveniente es buscar nivel por nivel hasta llegar a la salida, por lo que vamos a utilizar una búsqueda en amplitud.
Algo importante es que los términos “labyrinth” y “maze” se traducen ambos como laberinto al español pero en inglés tienen diferencias sutiles (aunque no siempre respetadas). El primero se refiere al mencionado en la mitología griega, en el cual estaba encerrado el minotauro. Entonces, por “labyrinth” se conocen los laberintos que tienen un solo camino Euleriano hacia al centro o de regreso (camino que visita todas las aristas sólo una vez, sección 10.7), mientras que “maze” describe a cualquier tipo de laberinto en el que intentamos llegar de una entrada a una salida, con lo que pueden existir opciones múltiples de dirección.
Teniendo un laberinto en el cual empezamos en el interior y buscamos la salida, uno de los algoritmos más conocidos para resolverlo es el conocido como de la “mano derecha” (o izquierda), y el cual consiste en simplemente mantener cualquiera de las dos manos pegada a la pared y avanzar hasta llegar a la salida. Este algoritmo funciona siempre que el laberinto tenga una conexión simple, lo que significa que todas las paredes están conectadas, y que exista una salida.
Cuando no todas las paredes están conectadas (supongamos que la pared que escogimos es parte de un rectángulo dentro del laberinto), existe una modificación conocida como el algoritmo de Pledge, el cual funciona de la siguiente manera: escogemos una dirección arbitraria para avanzar, y cuando llegamos a una pared, utilizamos el algoritmo de la mano derecha. En el momento que la suma angular de las vueltas que hemos dado se vuelva cero, soltamos la pared y continuamos con lo dirección que habíamos escogido. Este algoritmo funciona sólo para laberintos en segunda dimensión.
Problema ejemplo
Maestro de los Calabozos
Problema
¡Estás atrapado en un calabozo tridimensional y necesitas encontrar la forma más rápida de salir! El calabozo está forma por cubos que pueden o no estar ocupados por rocas. Toma un minuto moverse una unidad al norte, sur, este, oeste, arriba o abajo. No te puedes mover en diagonal y el calabozo está rodeado por piedra sólida.¿Es posible escapar? En caso de que lo sea, ¿cuál es el tiempo mínimo para hacerlo?
Entrada
La entrada consiste en varios calabozos. La descripción de cada calabozo empieza con una línea que contiene a los enteros l, r y c (todos tienen un tamaño máximo de 30).l es la cantidad de niveles en el calabozo.
r y c son la cantidad de filas y columnas que consta cada nivel del calabozo.
En seguida habrá l bloques de r líneas conteniendo cada una c caracteres. Cada caracter representa a una celda del calabozo. Una celda ocupado por una piedra está indicada por un caracter ‘#’ y una libre por el caracter ‘.’. Tu posición inicial está indicado por ‘S’ y la salida por ‘E’. Hay una línea en blanco después de cada nivel. La entrada termina con tres cero para l, r y c.
Salida
Por cada calabozo debes generar una línea a la salida. Si es posible alcanzar la salida, imprime una línea con el mensaje:Escaped in x minute(s).
donde x debe ser reemplazado por el tiempo más corto que toma escapar.
Si no es posible escapar, imprime la línea:
Trapped!
Solución: Estamos buscando la distancia más corta a la salida, por lo que vamos a utilizar una búsqueda en amplitud. El recorrido del laberinto lo realizamos de manera similar al del problema anterior.
Código

En las primeras cuatro líneas definimos la estructura posicion, la cual guarda las coordenadas (x, y, z) de la casilla y el tiempo t en el que llegamos. Las variables que vamos a utilizar están declaradas entre las líneas 6 y 11. El laberinto lo guardamos en la variable maze y en la variable vis guardamos si ya visitamos ese cuarto. El arreglo buffer es la cola que nos indica cual es la siguiente casilla a visitar. En pos_ini guardamos la posición inicial (las coordenadas de la casilla con la ‘S’). Los enteros i, j, y k los utilizamos para los ciclos, y l, r y c para guardar el tamaño del laberinto, según lo descrito en el problema.
Entre las líneas 13 y 23 tenemos el procedimiento agrega, el cual añade una nueva posición a considerar en la cola. Como parámetros tenemos n que es la posición del último elemento en la cola, nuevo que es el cuarto desde el que llegamos y dx, dy y dz que son el movimiento con el que llegamos.
La búsqueda en amplitud la realizamos en el procedimiento busca (líneas 25 a 51). El parámetro pos nos indica en que posición estamos, y como la declaramos con var, el valor de la variable que pasamos como parámetro también cambia. Las variables pa y pf nos indican la posición actual y la final en nuestra cola. Empezamos inicializando las posiciones (línea 28) y agregando a la cola la primera casilla (línea 29). Hasta que encontremos la salida (líneas 47 y 48), o hasta que no queden más casillas a visitar (línea 50), nos movemos a la siguiente posición en la cola (líneas 31 y 32), revisamos las posiciones adyacentes y si las podemos visitar, las agregamos a la cola (líneas 35 a 46).
Empezamos inicializando las casillas como no visitadas y como pared (líneas 57 y 58). Entre las líneas 59 y 77, leemos el laberinto y guardamos la posición desde donde iniciamos (líneas 66 a 72). Proseguimos buscando la salida (línea 78), y en caso de encontrarla escribimos en cuanto tiempo salimos (líneas 81 y 82); en caso de que no, escribimos que estamos atrapados (línea 80). Terminamos leyendo los tamaños del nuevo caso (línea 83).
Caso ejemplo
| Entrada: |
3 4 5 S.... .###. .##.. ###.# ##### ##### ##.## ##... ##### ##### #.### ####E 0 0 0 |
| Desarrollo: |
x y z, t 1 1 1, 0 2 1 1, 1 1 2 1, 1 3 1 1, 2 1 3 1, 2 4 1 1, 3 5 1 1, 4 5 2 1, 5 5 3 1, 6 4 3 1, 7 4 4 1, 8 4 4 2, 9 3 4 2, 10 5 4 2, 10 3 3 2, 11 5 4 3, 11 |
| Salida: | Escaped in 11 minute(s). |
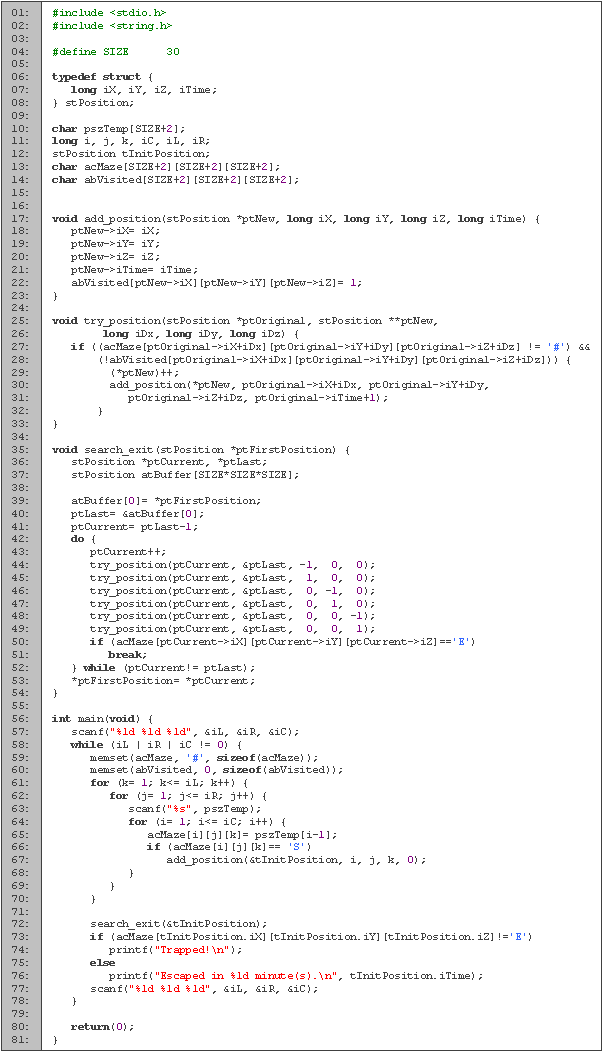
Código en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 01-May-2006 | 0.021 | 0.000 | 0.050 | 53.180 | Minimum |
| C | 11-Jun-2006 | 0.023 | Minimum | |||
 Componentes conexas (Floodfill)
Componentes conexas (Floodfill)
