Las podas (pruning) son formas de reducir la cantidad de vértices a visitar. La idea básica es dejar de visitar vértices con los que sabemos que no podemos llegar a un resultado óptimo. Como al no visitar un vértice dejamos de visitar toda la rama, efectuar podas en los primeros niveles reduce enormemente la cantidad de vértices a visitar.

Muchas veces las podas las realizamos por restricciones explícitas: el mismo problema nos las está dando (como en las siguientes dos secciones). En algunas otras son implícitas, por lo que las podemos deducir del resultado que estamos buscando y los resultados parciales que tenemos (como en el problema a continuación).

Cuando no necesitamos una respuesta óptima, sino cualquiera que sea razonablemente buena dentro de cierta tolerancia, también podemos hacer podas cuando parece que el vértice a visitar no es buena opción de acuerdo a criterios que nosotros establecemos. A esto se le conoce como heurística, y es particularmente útil para problemas cuyo árbol es demasiado grande para poder visitarlo completo (ya sea por limitantes en tiempo o memoria). Aunque como el resultado no es necesariamente el óptimo, no suelen ser utilizados en los concursos de programación.

Como vamos a ver en esta y en las siguientes secciones, a veces existen podas que son bastante simples ayudan a encontrar soluciones en tiempos comparativamente mucho más rápidos.




Solución: Aunque este problema es del tipo de la mochila (sección 8.6), al tener pocas piedras y con pesos muy grandes hacen que resolverlo mediante este enfoque no sea eficiente. Para solucionarlo mediante una búsqueda exhaustiva, vamos a utilizar un enfoque similar al de las permutaciones en donde agregamos las piedras que no hayamos utilizado. En las permutaciones revisamos el resultado hasta llegar a las hojas, pero en este caso el resultado puede estar en cada vértice. Aprovechando esto, podemos decidir cuales vértices podemos dejar de visitar para agilizar la búsqueda.





En las primeras cuatro líneas declaramos las variables a utilizar. La variable i es para ciclos, m es la diferencia mínima de pesos, n guarda la cantidad de datos y t es el peso total de las piedras.

En la función piedras (líneas 6 a 17) es donde calculamos la distribución óptima de las piedras en los dos montones. La variable i la utilizamos en los ciclos, mientras que p contiene el peso acumulado en el primer montón. Al igual que en las permutaciones, marcamos cuales piedras ya hemos utilizado y vamos agregando las que no (línea 10). La diferencia es que también incluimos otra restricción (la poda) en la cual dejamos de visitar las ramificaciones que no mejoran el resultado. Una vez que sabemos que la piedra mejora el resultado, lo incluimos, guardamos el resultado (línea 12) y vemos si podemos mejorar agregando otra piedra (línea 14).

En la última parte tenemos la parte principal del código (líneas 19 a 30). Empezamos leyendo la cantidad de piedras (línea 20), para después leer el peso de cada uno de ellas (línea 24). Cada vez que leemos un nuevo peso, incrementamos el total (línea 25). Igualamos el mínimo al total, ya que iniciamos con ninguna piedra en el primer montón (línea 27). Después mandamos llamar a la función piedras (línea 28), e imprimimos la mínima diferencia (línea 29).

Entrada:	5 5 8 13 27 14
Desarrollo:	t= 5 + 8 + 13 + 27 + 14 = 67 m= 67 p= 0,  m= 67   () p= 5,  m= 57   (5) p= 13, m= 41   (5,8) p= 26, m= 15   (5,8,13) p= 40, m= 13   (5,8,13,14) p= 32, m= 3    (5,13,14)
Salida:	3

Contando las veces que entra a la función, podemos ver como con la poda sólo lo hacemos 6 veces, mientras que si no la tuviéramos serían: 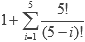 = 326 veces. Otra cosa que podemos observar es que intentar todas las combinaciones (entre poner un elemento o no) es O(2ⁿ), mientras que este tipo de búsquedas son O(n!), por lo que si no podamos (o no lo hacemos correctamente) este enfoque resulta significativamente más costoso.

Si queremos resolverlo generando todas las combinaciones, podemos hacerlo contando en base dos, donde un cero nos indica que no lo utilizamos y un uno que sí. Si queremos hacerlo mediante árboles, a cada nivel le asignamos un peso y las ramificaciones corresponden entre tomarlo o no.

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	02-May-2006	0.001	0.001	0.050	1.972	138
C	03-May-2006	0.015				150