Se conoce como coloreado de gráficas al problema de asignarle un color (que puede ser representado mediante un número o cualquier otra etiqueta) a determinados objetos dentro de una gráfica, comúnmente, a los vértices. Lo que se busca mediante la coloración es que alguna restricción de adyacencia o incidencia se cumpla.
Al número mínimo de colores que necesita una gráfica para que dos vértices adyacentes no compartan color, se le conoce como número cromático. Si una gráfica puede ser coloreada con k colores se dice que es k-coloreable, y si k es el menor posible, se dice que es k-cromática.
Saber si una gráfica es k-coloreable es un problema NP-completo, y obtener el número k para que sea k-cromática es un problema NP-difícil. Los únicos valores para los que el problema de k-coloreable no es un problema NP-completo es para k = 1 y 2, o para k = 4 si la gráfica corresponde a un mapa.
Problema ejemplo
Bicoloración
Problema
En 1976 el “El Teorema de los Cuatro Colores” fue demostrado con ayuda de una computadora. Este teorema indica que cualquier mapa puede ser coloreado utilizando solo cuatro colores, de tal forma que ninguna región está coloreada igual que alguna vecina.Aquí se te pide que resuelvas un problema mucho más sencillo. Debes decidir si una gráfica conexa arbitraria puede ser bicoloreada. Esto es, si se puede asignar colores (de una paleta de dos) a los vértices de tal forma que dos vértices adyacentes no compartan el mismo color. Para simplificar el problema puedes asumir que:
- Ningún vértice tiene una arista consigo mismo.
- La gráfica no es dirigida. Esto es, si un vértice a está conectado al vértice b, entonces debes asumir que b está conectado a a.
- La gráfica será fuertemente conexa. Esto es, siempre existirá por lo menos un camino entre un vértice dado a otro.
Entrada
La entrada consiste en varios casos prueba. Cada caso comienza con una línea que contiene a n (1 < n < 200), la cantidad de vértices distintos. La segunda línea contiene la cantidad de aristas l. Después, le siguen l líneas, cada una con dos enteros que especifican a los vértices que une la arista. Los vértices estarán etiquetados utilizando un número a (0 ≤ a < n).La entrada termina con el caso n = 0, el cual no deberá de ser procesado.
Salida
Deberás decidir si la gráfica de cada caso en la entrada es bicoloreable o no, e imprimirlo como se muestra en los ejemplos.
Solución: Para una gráfica conexa, podemos colorear el primer vértice con el color que queramos, después colorear sus vértices adyacentes con el otro color, y repetimos recursivamente los mismos pasos con estos vértices adyacentes.
Realizamos esto para todas las componentes de la gráfica. Si después de colorear, un vértice tiene dos colores, entonces la gráfica no es bicoloreable. Los colores que vamos a utilizar los representaremos mediante 1 y 2, además de 0 para indicar que todavía no ha sido coloreado.
Código

En las primeras cuatro líneas definimos las variables que vamos a utilizar. Para los ciclos utilizamos i; n y l los utilizamos según la descripción del problema, y x e y los utilizamos para leer los vértices adyacentes. El arreglo c nos sirve para guardar el color de cada vértice, y la matriz m es la matriz de adyacencia.
El siguiente procedimiento (líneas 6 a 17) es una búsqueda en profundidad para ir coloreando los vértices. El vértice en el que nos encontramos es p y la cantidad de vértices es n. Con cada vértice revisamos si existe una arista que lo conecte con p (línea 10), y de ser así, quitamos la arista (para no volverla a considerar), coloreamos el vértice y visitamos el nuevo vértice (líneas 12 a 15). La línea en que coloreamos (línea 14) puede resultar algo confusa. Como podemos pasar varias veces por un mismo vértice (y lo coloreamos cada vez que pasamos) utilizamos la operación OR. Como esta operación se realiza bit por bit, en los primeros dos bits guardamos cada uno de los colores. Para saber cual color es el siguiente, escribimos la suma de los colores (3) y le restamos el color actual.
En la función bicolorable (líneas 19 a 33) vemos si la gráfica lo es. Empezamos buscando todos los vértices que no han sido coloreados (líneas 23 y 24), los coloreamos (línea 26) y visitamos los vértices con los que es adyacente (línea 27). Como la búsqueda en profundidad recorre toda las gráficas conexas, la cantidad de veces que encuentre uno no coloreado será igual a la cantidad de componentes de la gráfica. En la siguiente línea inicializamos el resultado a true. Después revisamos cada vértice y si tiene dos colores, entonces la gráfica no es bicolorable (línea 31). Terminamos devolviendo el resultado.
Casos ejemplo
| Entrada: |
3 3 0 1 1 2 2 0 0 |
| Desarrollo: |
m[] 0 1 2 0 0 1 0 1 0 0 1 2 1 0 0 p c[] 0; 1 0 0 1; 1 2 0 2; 1 2 1 0; 3 2 1 |
| Salida: | NOT BICOLORABLE. |
| Entrada: |
5 4 0 1 0 2 0 3 0 4 0 |
| Desarrollo: |
m[] 0 1 2 3 4 0 0 1 1 1 1 1 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 4 0 0 0 0 0 p c[] 0; 1 0 0 0 0 1; 1 2 0 0 0 2; 1 2 2 0 0 3; 1 2 2 2 0 4; 1 2 2 2 2 |
| Salida: | BICOLORABLE. |
Código en C
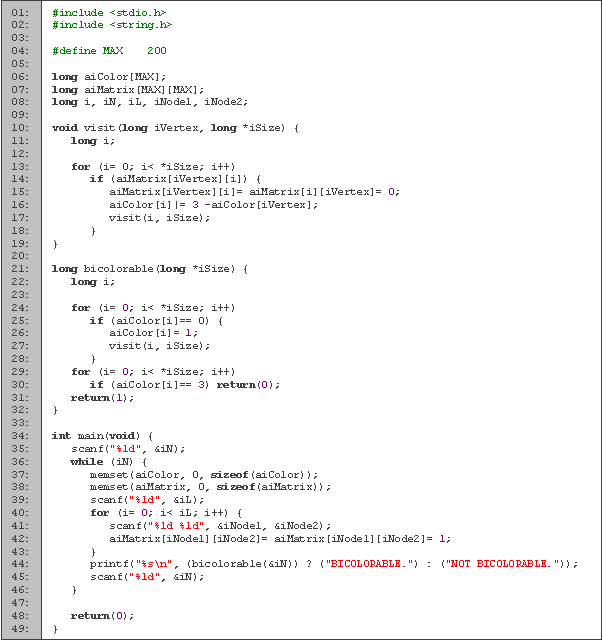
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 30-May-2006 | 0.002 | 0.000 | 0.004 | 9.576 | Minimum |
| C | 30-May-2006 | 0.002 | Minimum | |||
Otros problemas
Ural:
 Introducción
Introducción
