Llamamos camino Euleriano al camino que visita todas las aristas sólo una vez. Si el camino forma un ciclo, se le denomina ciclo Euleriano. Si una gráfica tiene un camino Euleriano, se dice que la gráfica es Euleriana. Se conocen con este nombre en honor a Leonhard Euler, quien fue el primero en estudiarlas al tratar de resolver el problema de los siete puentes de Königsberg.

La primera condición que necesitamos para que una gráfica sea Euleriana es que sea conexa. Si la gráfica es no dirigida, entonces todos los vértices deben tener grado par (para formar un ciclo) o sólo deben existir dos con grado impar (se puede formar un camino). Para las gráfica no dirigidas, necesitamos que la cantidad de aristas que entran sean igual a las que salen (para el ciclo), o que exista sólo un vértice que tenga una arista más que entra y sólo un vértice que con una más que salga (para el camino). Esto también aplica para multigráficas.

El algoritmo más conocido para construir un camino o ciclo Euleriano se le conoce como algoritmo de Fleury. Teniendo una gráfica Euleriana, tomamos un vértice con grado impar para empezar o cualquiera si no hay impares. Para escoger la arista a tomar, utilizamos cualquiera que no sea un puente a menos que no tengamos otra opción. Recordemos que un puente es una arista que al borrarla la gráfica se vuelve no-conexa. A la arista que tomamos, la borramos (o la hacemos no elegible). Repetimos este procedimiento hasta que no queden aristas. A la gráfica que le quitamos las aristas se le conoce como gráfica reducida.




Solución: A cada ficha de dominó la vamos a considerar como una arista. Para poder conectar todas las fichas en hilera, necesitamos que exista un camino que utilice todas las aristas (camino Euleriano).




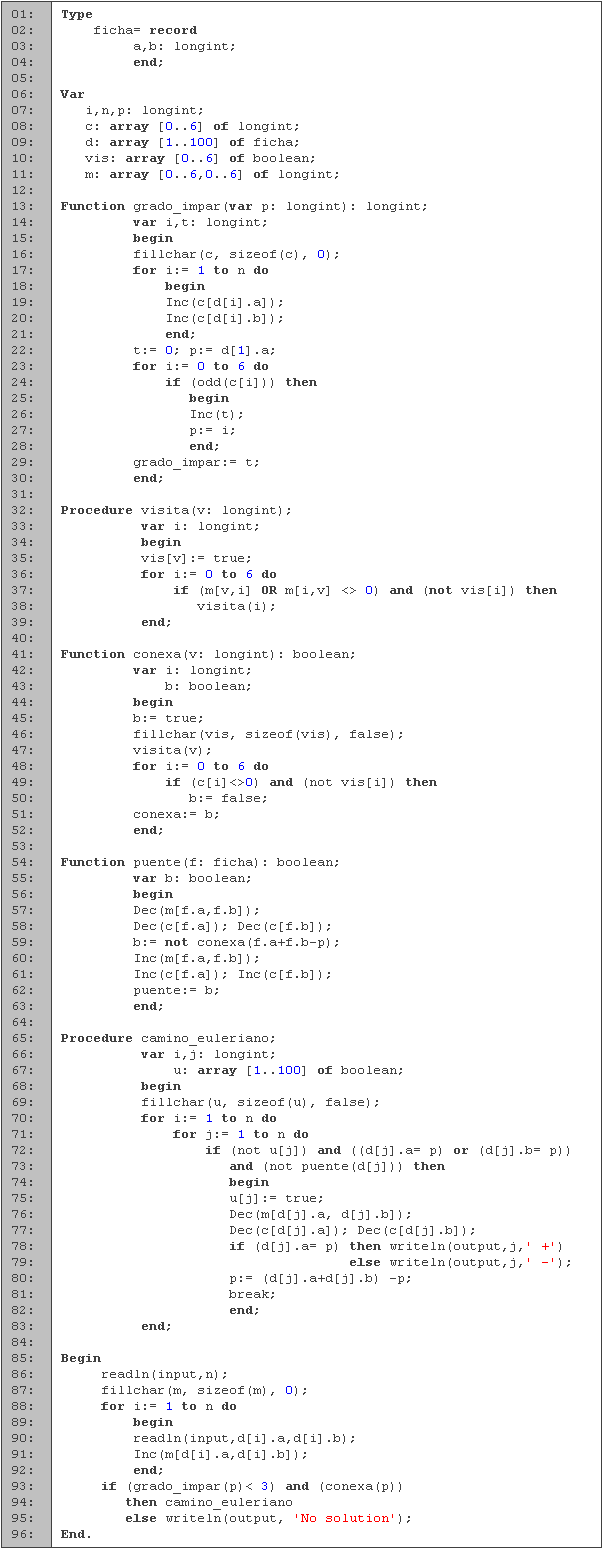
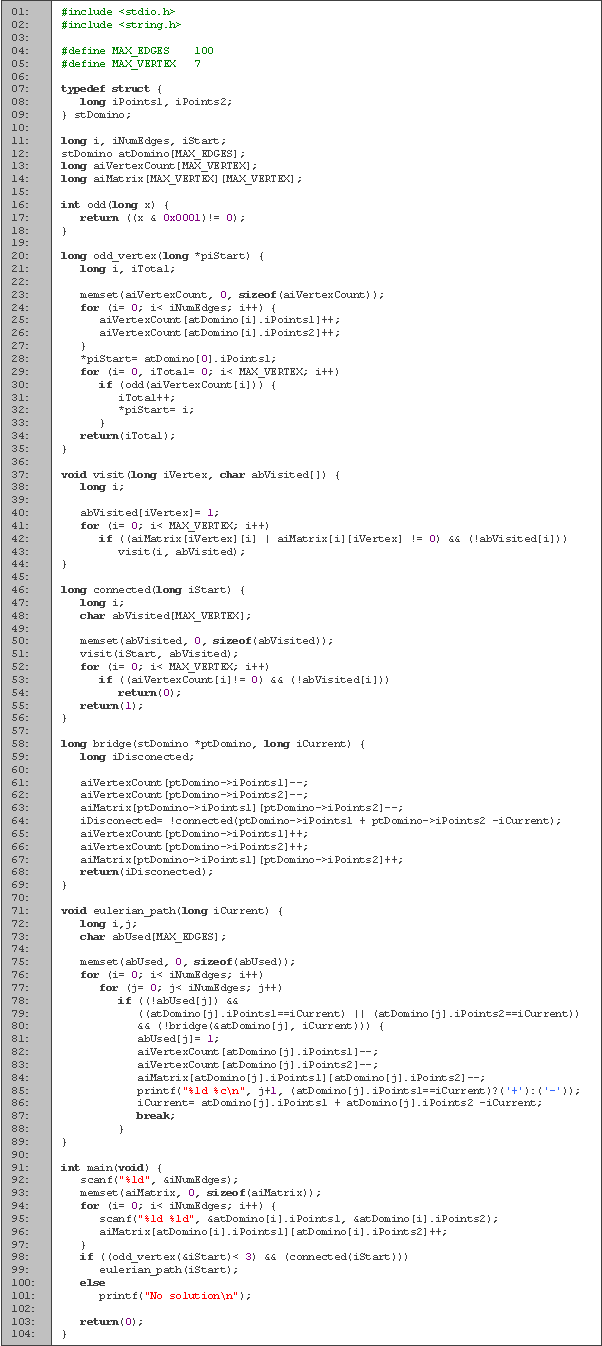
En las primeras cuatro líneas tenemos la definición de la estructura ficha, que corresponde a las fichas de dominó y que utilizaremos como aristas de la gráfica. Después tenemos la declaración de variables. Las fichas las leemos en d, m es la matriz de adyacencia, el arreglo vis lo usamos para saber cuales vértices ya utilizamos, y c para contar el grado de cada vértice. El entero i lo utilizamos para los ciclos, n para leer la cantidad de fichas y p para saber en que vértice estamos posicionados.

La primera función que tenemos es la de grado_impar (líneas 13 a 30), la cual nos devuelve la cantidad de vértices cuyo grado es impar. Al empezar, inicializamos todos los vértices como grado cero (línea 16), y enseguida incrementamos el grado cada uno de los vértices de las aristas (líneas 17 a 21).

Después contamos la cantidad de vértices impares en t, y cada que encontramos uno, le asignamos a p el valor de ese vértice (líneas 22 a 28). Por último, devolvemos la cantidad de vértices impares. En esta función vamos guardando el valor del último vértice impar en p para saber desde que vértice empezar a buscar el camino Euclidiano. En caso de que haya vértices impares, el valor de p será el del primer vértice de la primera arista.

En seguida tenemos la función conexa (líneas 41 a 42) y el procedimiento visita (líneas 32 a 39). La función conexa la utilizamos para saber si la gráfica es conexa, y esto lo hacemos mediante una búsqueda en profundidad que efectuamos en el procedimiento visita. En este último, lo que hacemos es revisar si el vértice tiene hijos que no hayamos visitado, y en caso de que los tenga, los visitamos y los marcamos. Entonces, para saber si la gráfica es conexa, realizamos la búsqueda a partir de cualquier vértice (en este caso v), y revisando que hayamos visitados los demás vértices (líneas 48 a 50). En caso de que no hayamos visitado alguno, entonces la gráfica no es conexa. También debemos de tener en cuenta de que no todos los números son usados como vértices (no todos los números aparecen en alguna ficha), por lo que si el grado del vértice es cero, es porque ese número no lo utilizamos.

Después tenemos la función puente (líneas 54 a 63), que determina si una arista es un puente. Pasamos como parámetro la variable f que es la arista que vamos a probar. Lo que hacemos es quitar la arista (líneas 57 y 58), y si la gráfica sigue siendo conexa es porque f no es un puente. Una vez que sabemos si es puente o no, volvemos a poner la arista (líneas 60 y 61) y devolvemos el resultado (línea 62).

El último procedimiento es camino_euleriano (líneas 65 a 83), y es donde encontramos dicho camino. Utilizamos el arreglo u para saber cuales aristas ya usamos (análogo a vis, solo que vis es para vértices). El ciclo de la línea 70 lo utilizamos para agregar todas las aristas, y el de la línea 71 para encontrar la arista actual. Una arista la agregamos si no la hemos usado anteriormente, si está conectada al vértice en el que nos encontramos (p) y si no es un puente. Una vez que se cumplan estas condiciones, marcamos la arista como usada (línea 75), decrementamos la matriz de adyacencia y el grado de cada vértice de la arista (líneas 76 y 77), escribimos cual ficha usamos y si la rotamos (líneas 78 y 79), nos movemos al vértice con el que conecta la arista (línea 80) y pasamos a buscar la siguiente arista (línea 81). Para saber a cual vértice nos movemos, sumamos los dos vértices de la arista y le restamos en el que estamos, entonces si el valor de p era d[j].a cambia a d[j].b y viceversa.

La parte principal del código la tenemos entre las líneas 85 y 96. Comenzamos leyendo la cantidad de piezas de dominó (línea 86) e inicializando la matriz de adyacencia a cero (línea 87). En seguida leemos todas las fichas, y actualizamos la matriz de adyacencia (líneas 88 a 92). Si la cantidad de vértices de grado impar son menores a tres y a la gráfica es conexa, entonces buscamos el camino euleriano; en caso contrario, imprimimos “No solution”.

Entrada:	5 1 2 2 4 2 4 6 4 2 1
Desarrollo:	0  1  2  3  4  5  6 c[]= 0, 2, 4, 0, 3, 0, 1 grado_impar: 2 1 → 2 → 4 → 6 conexa: TRUE  p   d[j] puente(d[j])  6:  6 4;   FALSE  4:  2 4;   FALSE  2:  1 2;   FALSE  1:  2 1;   FALSE  2:  2 4;   FALSE
Salida:	2 - 5 + 1 + 3 + 4 -

Un problema con el algoritmo de Fleury es que saber si una arista es puente o no, no es inmediato. Necesitamos quitarla y verificar que la gráfica siga siendo conexa, lo cual lleva bastante tiempo. Otro problema de la implementación es que para saber cuales aristas no hemos utilizado, tenemos que recorrer todo el arreglo buscándolas.

Podemos obtener un mejor algoritmo utilizando estructuras de datos de Conjuntos Disconexos. Una vez que sabemos si la gráfica es conexa y tiene a los más dos vértices de grado impar, empezamos por un vértice de grado impar (si no existen, por cualquiera), tomamos una arista y visitamos el siguiente vértices. Esto lo hacemos hasta que no podamos visitar otro vértice. Si al terminar todavía existen aristas que no hayamos utilizado, repetimos los pasos anteriores. Al final solo debemos unir todas las componentes en una sola. Si se implementa de manera correcta, este algoritmo tiene una complejidad O(E).

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	02-Jun-2006	0.020	0. 020	-	-	129
C	26-Jun-2006	0.064				362

Valladolid: