Contando con un arreglo de datos, queremos encontrar un subconjunto en este arreglo tal que sus datos estén en el mismo orden que en el arreglo, que cualquier elemento sea mayor a su predecesor y que dicho subconjunto sea el más grande que podamos encontrar. Por ejemplo, si tenemos la cadena “alfabeto” una subsucesión máxima creciente lo obtendríamos escogiendo las letras “alfabeto” con los que la subsucesión sería “abet” (aunque también podemos encontrar otras subcadenas de tamaño 4).
Suponiendo que ya tenemos la subsucesión máxima para todas las casillas hasta i, para conocer la subsucesión hasta i+1, buscamos todas las casillas que tengan menor valor a la actual y de entre estas tomamos la que tenga subsucesión máxima y agregamos la nueva casilla.
Problema ejemplo
Calificando la Historia
Muchos problemas en las Ciencias de la Computación involucran maximizar alguna medida de acuerdo a restricciones dadas. Considera un examen de historia en el cual se les pide a los alumnos ordenar ciertos eventos en orden cronológico. Los estudiantes que orden correctamente todos los eventos obtendrán una respuesta correcta, ¿pero como se deberán evaluar a los estudiantes que tuvieron mal uno o varios eventos?
Algunas posibilidades serían:
1.- 1 punto por cada evento que esté en la posición correcta.
2.- 1 punto por cada evento en la secuencia más larga (no necesariamente contigua) de eventos que se encuentran ordenados correctamente.
Por ejemplo, si cuatro eventos estuvieran ordenados correctamente como 1 2 3 4, entonces la respuesta 1 3 2 4 recibiría una puntuación de 2 utilizando el primer método (los eventos 1 y 4 están en la posición correcta) y una puntuación de 3 usando el segundo (las secuencias 1 2 4 y 1 3 4 están en orden correcto).
En este problema se te pide escribir un programa que califique este tipo de preguntas utilizando el segundo método.
Problema
Dado el orden cronológico correcto de n eventos 1, 2, …, n como c1, c2, …, cn donde 1 ≤ ci ≤ n denota la posición correcta del i-ésimo evento en orden cronológico, y una serie de respuestas de los estudiantes r1, r2, …,rn donde 1 ≤ ri ≤ n denota la posición cronológica dada por el estudiante al i-ésimo evento; determina la longitud de la secuencia de eventos (no necesariamente contigua) más larga que está en orden cronológico correcto.Entrada
La primera línea de la entrada consistirá en un entero n indicando la cantidad de eventos, donde 2 ≤ n ≤ 20. La segunda línea tendrá n enteros, indicando el orden cronológico correcto de los n eventos. Cada una de las líneas restantes contendrán n enteros, representado la ordenación que el estudiante le dio a los n eventos. Todas estas líneas contendrán n números en el rango [1..n], con cada número apareciendo solamente una vez en cada línea, y cada número separado de los demás en la línea por uno o más espacios.Salida
Para cada ordenación por parte de un estudiante, tu programa deberá imprimir la calificación de dicha ordenación. Deberá haber una línea de salida por cada ordenación de un estudiante.Solución: Nos piden que encontremos las subsucesión máxima creciente. El único inconveniente es que el orden no está dado por el valor de los números sino por el acomodo que tengan en la primera línea.
Código
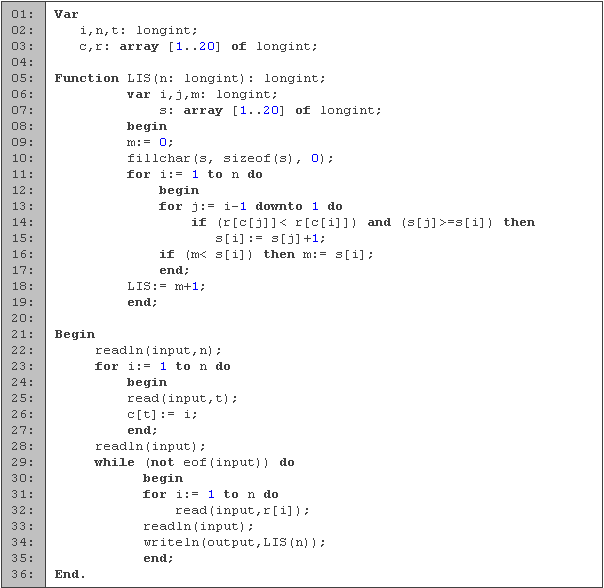
En las primeras tres líneas tenemos la declaración de variables. El entero i lo vamos a utilizar en ciclos, n para la cantidad de fechas, y t como variable temporal. En el arreglo c no guardamos el orden cronológico, sino que guardamos valor de cada fecha, y en r la respuesta que dio el alumno.
Entre las líneas 5 y 19 tenemos la función que encuentra el tamaño de la subsucesión máxima creciente. Las variables i y j las utilizamos para los ciclos, m para guardar el máximo, y el arreglo s para guardar el máximo hasta cada casilla. Empezamos inicializando las variables a cero (líneas 9 y 10). En seguida, para cada arreglo de la casilla, buscamos los que sean menores y el máximo hasta esa casilla sea mayor al que tenemos (líneas 13 a 15). Después revisamos si necesitamos actualizar el valor de m (línea 16). Terminamos devolviendo el tamaño máximo. Agregamos uno al resultado, ya que como inicializamos a cero, no estaríamos considerando al último elemento como parte de la subsucesión.
En la parte principal del código (líneas 21 a 36), empezamos leyendo la cantidad de datos que contiene cada sucesión (línea 22) y después leemos el orden correcto de las fechas (líneas 23 a 28). Al leer una fecha (línea 25), le asignamos un valor de acuerdo a la posición en que la encontramos (línea 26). A continuación leemos una sucesión (líneas 31 a 33) e imprimimos el tamaño de su subsucesión máxima creciente. En Pascal es muy importante tener un readln (líneas 28 y 33) para poder encontrar el fin de archivo (si no se lee el fin de línea, no se encuentra el fin de archivo, aunque no hayan más datos).Caso ejemplo
| Entrada: |
5 3 1 2 5 4 1 2 3 4 5 5 2 3 1 4 |
| Desarrollo: |
c[] = 2, 3, 1, 5, 4 r[c[]]= 2, 3, 1, 5, 4 2 ; s[1]= 0 ; m= 0 2, 3 ; s[2]= s[1]+1= 1; m= 1 2, 3, 1 ; s[3]= 0 ; m= 1 2, 3, 1, 5 ; s[4]= s[2]+1= 2; m= 2 2, 3, 1, 5, 4 ; s[5]= s[2]+1= 2; m= 2 r[c[]]= 2, 3, 5, 4, 1 2 ; s[1]= 0 ; m= 0 2, 3 ; s[2]= s[1]+1= 1; m= 1 2, 3, 5 ; s[2]= s[2]+1= 2; m= 2 2, 3, 5, 4 ; s[3]= s[2]+1= 2; m= 2 2, 3, 5, 4, 1 ; s[4]= 0 ; m= 2 |
| Salida: |
3 3 |
Disminuyendo la complejidad
Está claro que el tiempo de ejecución de este algoritmo es O(n2), dado que tenemos dos ciclos anidados (líneas 11 y 13). Podemos encontrar un algoritmo más rápido, basándonos en los valores que toma s.
Para tener una subsucesión de tamaño s, primero debimos de haber encontrado una de tamaño s-1, y dentro de todas la subsucesión de tamaño s-1, la más útil para encontrar la de tamaño s en la que su último elemento es más pequeño. Si guardamos los elementos menores para todos los valores que puede tomar s, nos daremos cuenta que están ordenados de forma creciente y es lo que vamos a aprovechar.
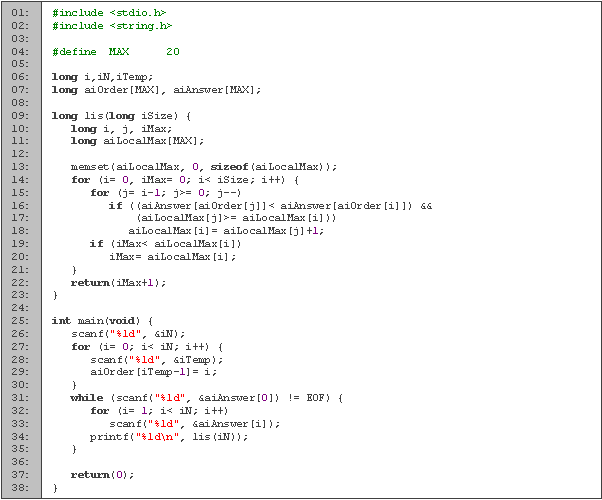
Utilizamos las mismas variables que en la primera implementación, y agregamos la variable l, que es donde vamos a guardar el menor elemento para cada tamaño posible de la subsucesión.
Entre las líneas 4 y 16 tenemos una función que realiza la búsqueda binaria. La implementación es muy similar a la de la sección 3.7, pero con la diferencia de que si no encuentra el valor que estamos buscando (x), devuelve el número que sea mayor y más cercano a él.
En la siguiente función es donde buscamos la subsucesión máxima creciente (líneas 18 a 30). Empezamos inicializando m a cero y cada casilla de l a infinito (para efectos prácticos, cualquier valor mayor que n). Buscamos en que posición el elemento actual es mayor que todos los anteriores (línea 25), asignamos este elemento como nuevo mínimo de tamaño s (ya que si fuera mayor, no estaríamos en esta casilla) y revisamos si encontramos una subsucesión mayor a nuestro máximo actual (línea 27). Terminamos devolviendo el tamaño máximo (línea 29).
Caso ejemplo (bis)
| Entrada: |
5 3 1 2 5 4 1 2 3 4 5 5 2 3 1 4 |
| Desarrollo: |
c[] = 2, 3, 1, 5, 4 r[c[]]= 2, 3, 1, 5, 4 l[] ∞ ∞ ∞ ∞ ∞; 2 ∞ ∞ ∞ ∞; s= 1; m= 1; 2 3 ∞ ∞ ∞; s= 2; m= 2; 1 3 ∞ ∞ ∞; s= 1; m= 2; 1 3 5 ∞ ∞; s= 3; m= 3; 1 3 4 ∞ ∞; s= 3; m= 3; r[c[]]= 2, 3, 5, 4, 1 l[] ∞ ∞ ∞ ∞ ∞; 2 ∞ ∞ ∞ ∞; s= 1; m= 1; 2 3 ∞ ∞ ∞; s= 2; m= 2; 2 3 5 ∞ ∞; s= 3; m= 3; 2 3 4 ∞ ∞; s= 3; m= 3; 1 3 4 ∞ ∞; s= 1; m= 3; |
| Salida: |
3 3 |
Códigos en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 06-Jun-2006 | 0.021 | 0.000 | 0.030 | 23.550 | Minimum |
| C | 10-Jun-2006 | 0.020 | Minimum | |||
| Pascal | 07-Jun-2006 | 0.020 | Minimum | |||
| C | 10-Jun-2006 | 0.016 | Minimum | |||
Otros problemas
Valladolid:
Intervalo de suma máxima
