Una permutación la podemos ver como una de las distintas formas de ordenar un conjunto finito que tengamos. También lo podemos definir como una sucesión de todos los elementos del conjunto, utilizándolos sólo una vez; o como la biyección del conjunto a si mismo.

La importancia de encontrar un algoritmo eficiente para las permutaciones deriva de que en muchos problemas la solución depende del orden en que estén acomodados los datos, por lo que si necesitamos hacer una búsqueda exhaustiva para encontrara una solución óptima, es conveniente conocer la mejor forma para generar los distintos acomodos.




Solución: Para generar todas las permutaciones, podemos crear un árbol en el que cada vértice tiene una letra, excepto la raíz que está vacía, y desde cada vértice ramificamos a las letras que no hayamos utilizado en el camino desde la raíz. Si los vértices los vamos agregando en orden lexicográfico, al final el resultado también estará ordenado.

Este algoritmo funciona bien cuando no tenemos letras repetidas. En caso de que la cadena si contenga elementos repetidos, lo que hacemos es revisar si la permutación actual es menor o igual que la anterior, y de ser así, no la utilizamos.





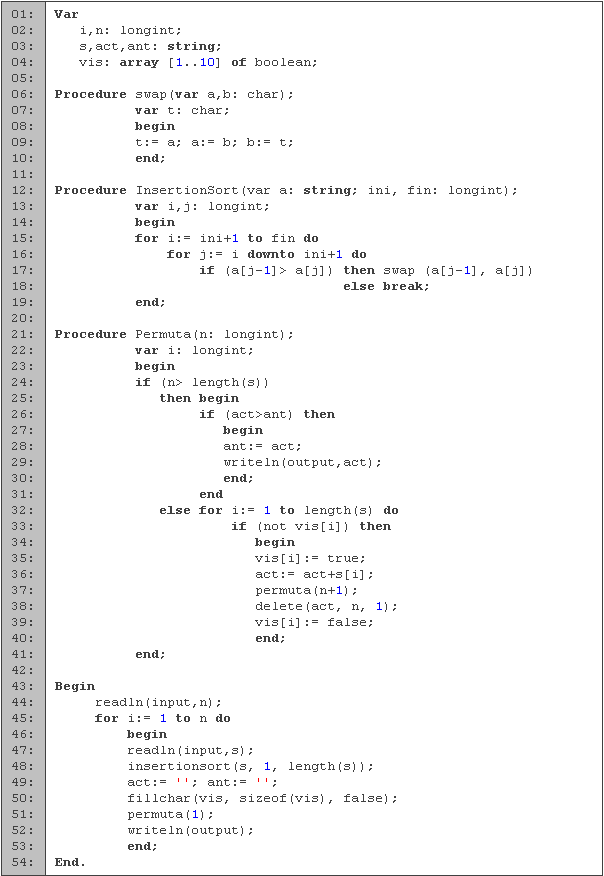
Empezamos declarando en las primeras tres líneas las variables que vamos a utilizar. En la cadena s leemos la palabra a permutar, en act guardamos la permutación actual y en ant la anterior. En el entero i lo utilizamos para los ciclos y en n leemos la cantidad de cadenas a procesar. El arreglo booleano vis lo utilizamos para saber cuales caracteres ya utilizamos.

El primer procedimiento, swap (líneas 6 a 10), lo utilizamos para intercambiar los valores de dos caracteres. En seguida tenemos el procedimiento insertionsort (líneas 12 a 19) que funciona de manera similar al que utilizamos en la sección 3.2, con la diferencia de que incluimos como parámetros entre que casillas vamos a ordenar (ordenamos entre ini y fin).

En el procedimiento permuta de las líneas 21 a 41 es donde encontramos todas las permutaciones de la cadena. El parámetro n nos indica en que nivel del árbol nos encontramos. Si el nivel es mayor a la cantidad de letras (líneas 24 a 31), es porque ya las utilizamos todas. Vemos si la permutación actual es mayor que la anterior (línea 26), y de ser así, imprimimos la cadena y actualizamos el anterior (líneas 28 y 29). En caso de que todavía no hayamos utilizado todas las letras, buscamos que letra no ha sido usada (líneas 32 y 33) y una vez que encontremos alguna, la agregamos a la permutación, la ponemos como usada y buscamos la siguiente letra a utilizar (líneas 36 a 37). Al volver del procedimiento, quitamos la letra y la regresamos a no usada (líneas 38 y 39) para intentarlo con otras.

La comparación que hacemos en la línea 26, la podemos ir haciendo en niveles anteriores con lo que nos evitaríamos tener que llegar hasta la hoja para revisar si la permutación no la habíamos impreso anteriormente. Revisar la solución antes de llegar a las hojas para dejar de visitar ramas se le conoce como poda, y lo veremos más a fondo en la siguiente sección.

La parte principal del código la encontramos entre las líneas 43 a 54. Empezamos leyendo la cantidad de cadenas a permutar (línea 44). Para cada caso, leemos la cadena (línea 47), la ordenamos de menor a mayor (línea 48), inicializamos las variables (líneas 49 y 50) y mandamos permutar la cadena (línea 51).

Entrada:	1 aba
Desarrollo:	act     ant 'aab' > ''    ← 'aba' > 'aab' ← 'aab' < 'aba' 'aba' = 'aba' 'baa' > 'aba' ← 'baa' = 'baa'
Salida:	aab aba baa

También existen formas de encontrar todas las permutaciones de forma iterativa. Una de ellas es encontrando la manera de obtener la siguiente permutación de una cadena.

La siguiente permutación la obtenemos haciendo lo siguiente: teniendo una cadena de longitud n, primero buscamos de derecha a izquierda por el primer caracter que sea menor al anterior, y a la posición en que se encuentra la llamaremos i. Una vez que lo encontramos, lo cambiamos de posición con el carácter de menor valor que sea mayor a este, y que está en el intervalo [i+1, n]. Terminamos ordenando el intervalo [i+1, n].


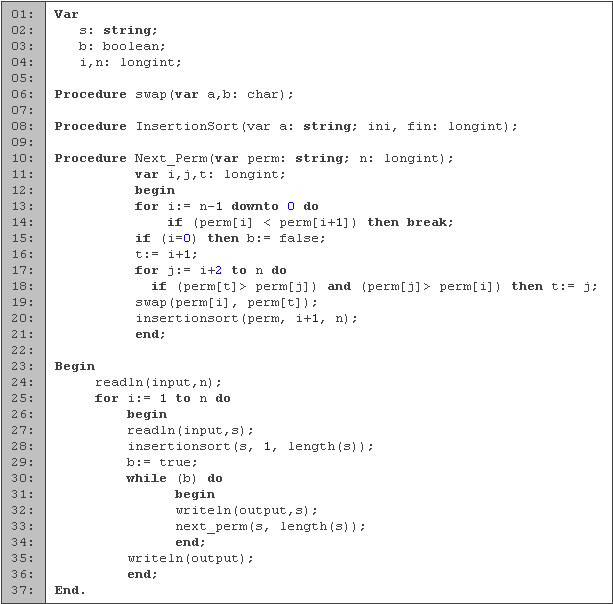
Las variables i, n y s las utilizamos de manera análoga al código anterior. El booleano b lo usamos para saber cuando la cadena ya no tiene una siguiente permutación. Los procedimientos de las líneas 6 y 8 también son los mismos del código anterior.

En el procedimiento que se encuentra entre las líneas 10 y 21 calculamos la siguiente permutación de la cadena perm de longitud n. Los enteros i y j los utilizamos para los ciclos, y a t como variable temporal. Entre las líneas 13 y 14 buscamos el primer número que es mayor que el anterior, yendo del fin al inicio de la cadena. Si no lo encontramos, es por que perm es la última permutación (línea 15). Una vez que lo tengamos, buscamos al menor de los elementos que sea mayor que este y que se encuentre después de él (líneas 16 a 18), e intercambiamos los lugares de ellos (línea 19). Terminamos ordenando a los elementos restantes.

Los cambios en la parte principal del código los encontramos entre las líneas 29 y 34. Lo que hacemos es generar la siguiente permutación e imprimirla hasta que no existan más.

Entrada:	1 abac
Desarrollo:	s     i  t aabc   3  4 aacb   2  4 abac   3  4 abca   2  3 acab   3  4 acba   1  3 baac   3  4 baca   2  3 bcaa   1  2 caab   3  4 caba   2  3 cbaa   0
Salida:	aabc aacb abac abca acab acba baac baca bcaa caab caba cbaa

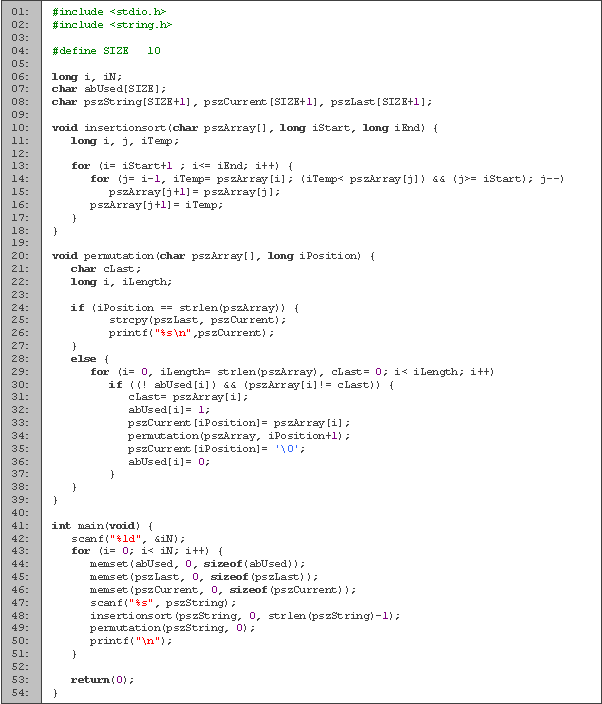
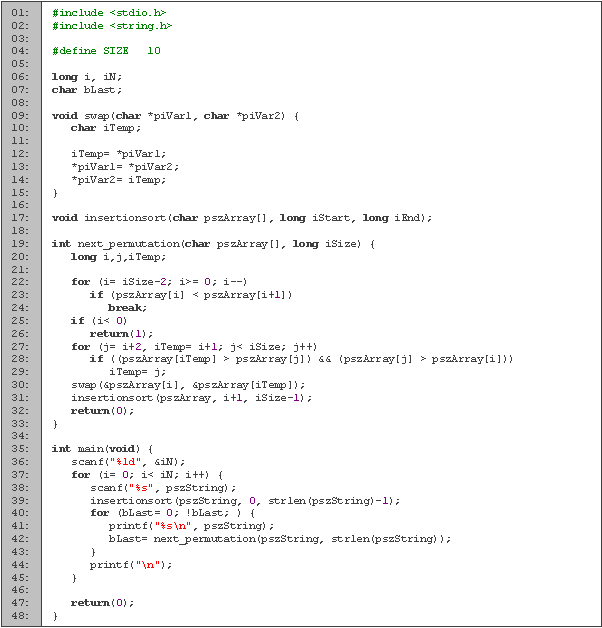
Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	02-May-2006	6.822	0.043	0.816	9.691	316
C	24-Jun-2006	0.623				388
Pascal	02-May-2006	2.947				316
C	03-May-2006	0.361				388