Introducción

Una gráfica (también llamada grafo) es un método para representar objetos, donde lo que nos interesa es la forma en que están relacionados entre sí. La rama de las matemáticas que se encarga de su estudia se le conoce como Teoría de las Gráficas y es una rama de las matemáticas combinatorias. El ejemplo más común es la representación de una ciudad, donde nos interesa conocer la forma para llegar de un lugar a otro mediante conexiones (calles), aunque se puede utilizar para modelar una gran variedad de problemas.

Una gráfica está compuesta por vértices (también llamados nodos) y aristas. Los vértices son los objetos que deseamos representar, mientras que las aristas son la forma en que están interconectadas. Se acostumbra representar a un vértice como un punto o un círculo y a una arista como una línea, no obstante, podemos elegir cualquier representación que nos convenga ya que las propiedades de la gráfica no cambian.

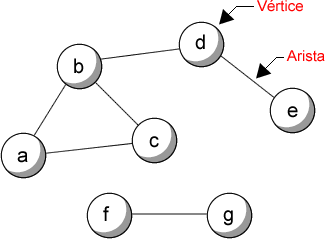Figura 10.1: Ejemplo y terminología de una gráfica

Decimos que dos vértices son adyacentes si comparten una arista. Cuando un vértice es adyacente a sí mismo, tiene un lazo (o bucle). El grado de un vértice es la cantidad de aristas conectadas a este (en el caso de un lazo, se cuenta dos veces). Una arista es incidente a un vértice si lo une con otro. Un vértice está aislado si no tiene una arista incidente (con lo que su grado es cero).

Dentro de una gráfica, pueden existir vértices que estén unidos por más de una arista. Si esto sucede, o si la gráfica incluye lazos, decimos que se trata de una multigráfica. A veces se utiliza el término multigráfica cuando no incluye lazos y pseudográfica cuando sí. En caso de que no contenga ni lazos ni aristas múltiples entre dos vértices, decimos que la gráfica es simple. Cuando en la gráfica sólo existe un vértice (sin aristas), a la gráfica se le llama trivial. Si no existen ni vértices ni aristas, la gráfica es nula.

En una gráfica, le llamamos camino a una sucesión de vértices y aristas que utilizamos para llegar de un vértice a otro, y si no pasamos por una arista más de una vez, el camino es simple. Decimos que un vértice es alcanzable desde otro si existe un camino entre los dos.

Si para cada pareja posible de vértices de la gráfica existe un camino (son alcanzables), entonces se le conoce como una gráfica conexa, y si esto no se cumple, se dice que la gráfica es no conexa. Teniendo una gráfica no conexa, a cada parte de la gráfica que sí es conexa se le conoce como componente conexa. Un puente es una arista dentro de una gráfica conexa, que al quitarla hace que la gráfica deje de serlo.

Un camino que empieza y termina en el mismo lugar se le conoce como circuito, y en el caso de que el camino sea simple entonces el ciclo también es simple. A las gráficas conexas que no contienen circuitos, se le conoce como árboles. A un grupo de árboles no-conexos se les conoce como bosque.

Cuando nombramos a los vértices o a las aristas, decimos que la gráfica es etiquetada. También podemos tener que el vértice posea dirección o peso. A las gráficas en las que las aristas tienen dirección se les nombra como gráficas dirigidas o digráficas, en caso contrario se les llama gráficas no dirigidas. Cuando tienen dirección, a las aristas también se les conoce como arcos (o flechas). A las gráficas con pesos se les conoce como ponderadas. Si la gráfica es dirigida y ponderada, se le llama red. A una gráfica dirigida en la que se pueda encontrar un camino entre cualesquiera dos vértices, se le conoce como fuertemente conexa.

La cantidad de vértices de una gráfica se representa con V y a la cantidad de aristas con E (por su nombre en inglés). Si en la gráfica E ≥ V, entonces debe haber por lo menos un ciclo. Si E < V -1, entonces la gráfica es forzosamente no conexa. En un árbol tenemos que E = V -1, aunque no todas las gráficas que cumplen la ecuación son árboles (solamente las conexas).

Si la gráfica es simple, la cantidad máxima de aristas que puede tener es

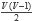. Cuando el número de aristas es igual a este valor, decimos que la gráfica es completa. Si el valor es igual o está muy cerca, decimos que la gráfica es densa. Y cuando tiene muy pocas aristas, decimos que la gráfica es dispersa. Aunque el saber si una gráfica es densa o dispersa es importante al elegir tanto un algoritmo como la forma de representar la gráfica, no existe un valor específico que delimite estos dos términos.

Para representan las gráficas para su uso dentro de un programa lo podemos hacer a través de sus vértices o a través de sus aristas. Generalmente los vértices van numerados, por lo que lo que nos interesa es la forma de guardar los vértices.

La primera forma es guardar en una lista las aristas. En cada casilla del arreglo tenemos dos valores, que son los vértices que conecta la arista. Se pueden incluir datos adicionales, como el peso. Para la gráfica ejemplificada arriba tendríamos (considerando que el vértice a lo tomamos como el primero, b el segundo y así sucesivamente):

	E₁	E₂	E₃	E₄	E₅	E₆
V_i	1	2	1	2	7	4
V_j	2	3	3	4	6	5

Otra forma para representar la gráfica es mediante una matriz de adyacencia. Cada renglón y columna representan un vértice, y la matriz representa la forma en que están conectados (comúnmente pesos o número de conexiones). Para el ejemplo anterior, tendríamos:

	V₁	V₂	V₃	V₄	V₅	V₆	V₇
V₁	0	1	1	0	0	0	0
V₂	1	0	1	1	0	0	0
V₃	1	1	0	0	0	0	0
V₄	0	1	0	0	1	0	0
V₅	0	0	0	1	0	0	0
V₆	0	0	0	0	0	0	1
V₇	0	0	0	0	0	1	0

Algo interesante de esta representación, es que si elevamos la matriz de adyacencia a la n-ésima potencia, en la casilla (i, j) tenemos la cantidad de caminos con los que se puede llegar desde el vértice i hasta el j, pasando por n aristas.

Otra representación es mediante una lista de adyacencia. En un arreglo, cada casilla representa un vértice y le vamos anexando los vértices con los que es adyacente. Esto lo podemos hacer también con una matriz, pero es más eficiente utilizando listas enlazadas. Siguiendo con el mismo ejemplo:

	Vértices Adyacentes
V₁	2, 3
V₂	1, 3, 4
V₃	1, 2
V₄	2, 5
V₅	4
V₆	7
V₇	6

La decisión para cual escoger dependerá en gran medida del algoritmo a utilizar y la cantidad de vértices (V), aristas (E) y grado máximo de un vértice (G) del problema. En la siguiente tabla podemos ver una comparación entre estas representaciones:

	Lista Aristas	Matriz de Adyacencia	Lista de Adyacencia
Espacio (memoria)	2E	V²	2E
Revisar adyacencia	E	1	G
Encontrar todos los adyacentes	E	V	G
Agregar arista	1	1	1
Borrar arista	E	2	2G