Teniendo una gráfica conexa, llamamos punto de articulación a todos los vértices que siendo borrado ocasionarían que la gráfica dejara de ser conexa (podemos decir que es el equivalente en vértice a los puentes). Cuando una gráfica no contiene puntos de articulación se dice que es “dos conexa”.

Para encontrar todos los puntos de articulación de una gráfica conexa, podemos utilizar una búsqueda en profundidad y realizar algunas operaciones adicionales. Al realizar la búsqueda en profundidad de la gráfica, nos van a sobrar aristas (que son las que formarían ciclos en el árbol de búsqueda). A estas aristas sobrantes las llamaremos aristas de conexión.

En el caso particular de un árbol, sabemos que un vértice es punto de articulación si al tomarlo como raíz tiene más de un hijo (ya que al quitarlo, cada hijo se convertiría en raíz de un árbol). En general, un vértice es un punto de articulación si, al realizar la búsqueda en profundidad, no podemos encontrar para cada uno de sus hijos un vértice descendiente (nivel menor) que comparta una arista de conexión con un vértice ascendente (nivel mayor, incluyendo al padre), con lo que habría un camino alterno para llegar. Esto cumple para cualquier vértice, excepto la raíz de la búsqueda. Para saber si la raíz es punto de articulación, sólo debemos contar sus hijos de manera análoga a un árbol, pero recordando no incluir los que están unidos por una arista de conexión. Por ejemplo:

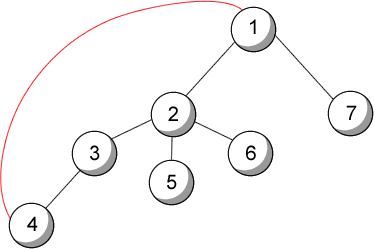Figura 10.2: Gráfica con puntos de articulación en 1 y 2, y arista de conexión entre 1 y 4

En esta gráfica, la raíz (1) es punto de articulación porque tiene dos hijos (2 y 7). Para el vértice 2, aunque su hijo 3 no cumple la condición porque 4 tiene una arista de conexión con 1, como 5 y 6 cumplen entonces también es punto de articulación. Sólo los vértices 1 y 2 son puntos de articulación.




Solución: Según la descripción del problema, los lugares críticos son los que desconectan la gráfica, por lo que son puntos de articulación. Entonces, lo que buscamos son todos los puntos de articulación en la gráfica.




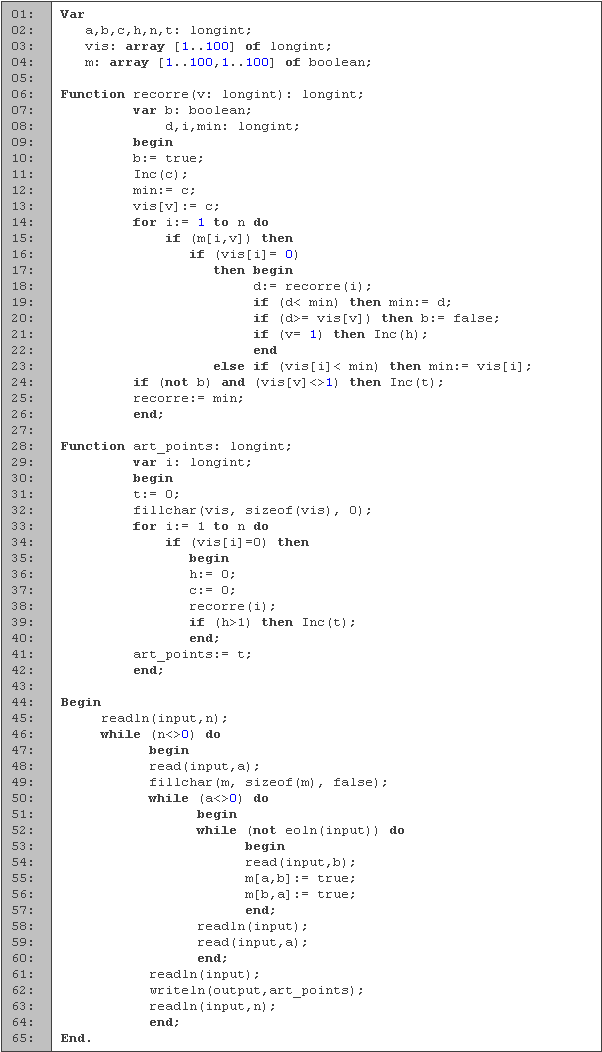
Empezamos declarando las variables que vamos a utilizar. Al igual que en problemas anteriores, el arreglo m va a ser la matriz de adyacencia y el arreglo vis lo utilizamos para saber si un vértice ya lo utilizamos. Los enteros a y b los vamos a usar para leer los vértices de las aristas, n para saber cuantos lugares hay, h para saber cuantos hijos tiene la raíz, c para numerar los vértices de acuerdo al orden en que los recorremos y t para contar la cantidad de puntos de articulación.

  La función recorre (líneas 6 a 26) realiza una búsqueda en profundidad modificada. Como parámetro tenemos v, que es el vértice que estamos visitando, y la función devuelve el valor mínimo de los vértices con los que está conectado. El booleano b nos sirve para saber si todos los hijos del vértice tienen una conexión arriba, el entero i los usamos para los ciclos, d como variable temporal y min para guardar el vértice mínimo con el que está conectado. Como ya habíamos visto, el arreglo vis los usaremos para saber si un vértice ya lo utilizamos, pero le agregaremos que si ya lo visitamos guarde el valor de en que momento lo visitamos.

Empezamos inicializando a b como verdadero (línea 10), incrementando la numeración del vértice en el que vamos (línea 11), y asignando este valor a vis (para saber cuando lo visitamos) y a min (porque la conexión más alta que tiene en este momento es consigo mismo). Después recorremos todos los vértices, y si tiene conexión con el actual (línea 15), revisamos si no lo hemos visitado (línea 16). En caso de que lo hayamos hecho, vemos si la conexión con este vértice es menor a la que teníamos (línea 23); en caso contrario, visitamos el vértice y al regresar examinamos si alguno de los hijos tiene una conexión con un vértice menor al que tenemos (línea 19), si algunos de los hijos no tiene conexión con un vértice mayor al actual lo marcamos en b (línea 20), y si el vértice actual es la raíz, incrementamos la cantidad de hijos (línea 21). Después de visitar todos los vértices, si alguno de los hijos no tiene conexión con alguno menor, entonces es un punto de articulación a menos de que estemos en la raíz (línea 24). Terminamos devolviendo el valor de min.

Los puntos de articulación los obtenemos en la función que se encuentra entre las líneas 28 y 42. Empezamos inicializando la cantidad de estos puntos a cero (línea 31), y a los vértices como no visitados (línea 32). Recorremos todos los vértices, y en caso de que no hayamos visitado alguno, inicializamos tanto la cantidad de hijos de la raíz como el contador de vértices a cero (líneas 36 y 37), y realizamos la búsqueda en profundidad. Después de realizar la búsqueda, si la raíz tiene más de un hijo incrementamos la cantidad de puntos (línea 39). Terminamos devolviendo el total (línea 41). El ciclo de la línea 33 nos ayuda a encontrar los puntos de articulación en todas las componentes de la gráfica, por lo que si la gráfica es conexa no lo necesitamos.

La parte principal del código la tenemos entre las líneas 44 y 65. Al comenzar leemos la cantidad de lugares (línea 45). Mientras sea distinto de cero, leemos la gráfica y encontramos sus puntos de articulación.

Entrada:	5 5 1 2 3 4 0 6 2 1 3 5 4 6 2 0 0
Desarrollo:	v  min   b         vis[]  1:  1  TRUE;   1, 0, 0, 0, 0  5:  1  TRUE;   1, 0, 0, 0, 2 ←  2:  2  FALSE;  1, 3, 0, 0, 2  3:  2  FALSE;  1, 3, 4, 0, 2  4:  2  FALSE;  1, 3, 4, 5, 2  v  min   b         vis[]  1:  1  TRUE;   1, 0, 0, 0, 0, 0  2:  1  TRUE;   1, 2, 0, 0, 0, 0 ←  3:  2  FALSE;  1, 2, 3, 0, 0, 0  5:  2  TRUE;   1, 2, 3, 0, 4, 0 ←  4:  4  FALSE;  1, 2, 3, 5, 4, 0  6:  4  FALSE;  1, 2, 3, 5, 4, 6
Salida:	1 2

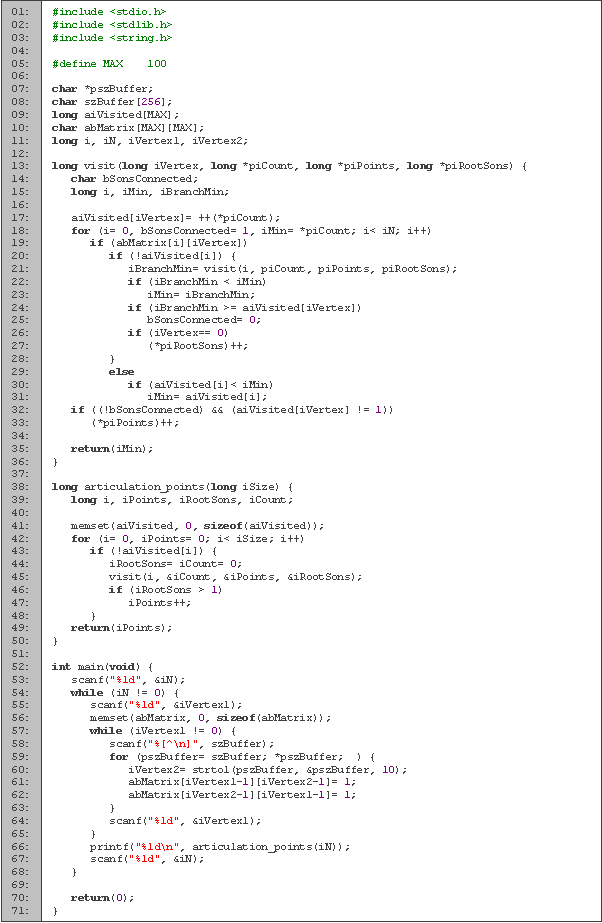
Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	31-May-2006	0.029	0.004	0.650	79.110	Minimum
C	26-Jun-2006	0.035				Minimum

Valladolid: