Problema 2
Fibokarel
fibo.txt
Una sucesión de números muy famosa fue creada por Fibonacci. Fibonacci (que significa hijo de Bonacci) es el apodo de Leonardo de Pisa, matemático italiano que vivió entre 1170 y 1270 de nuestra era. Esta sucesión se construye de la siguiente forma: El primero y segundo término son uno, los siguientes términos, se obtienen a partir de la suma de los dos términos anteriores. Así pues, los primeros ocho términos de la sucesión son: 1, 1, 2, 3, 5, 8, 13 y 21.
Los matemáticos generalizaron la sucesión de Fibonnacci, y a cualquier sucesión en que todo término, a partir del tercero, sea la suma de sus dos términos anteriores se le denomina Sucesión tipo Fibonacci. Lo anterior se puede escribir simbólicamente como: c1 = A, c2 = B y cn+1 = cn + cn-1. Por ejemplo si A = 5, B = 9, los primeros seis términos de la sucesión son 5, 9, 14, 23, 37 y 60.
Ayuda a Karel a construir sucesiones tipo Fibonacci dados los dos primeros términos A y B.
Problema
Construir, dados los primeros dos términos, la sucesión de Fibonacci.
Consideraciones
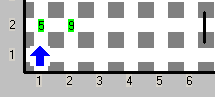
1) Al inicio hay A zumbadores en la celda (1, 2) y B zumbadores en la (2, 2). El resto de las celdas están vacías.
2) Sólo hay una pared en el mundo y está en el renglón 2, en algún lugar a la derecha de la celda (2, 2).
3) No se sabe la posición ni orientación inicial de Karel.
4) Al inicio Karel tiene una infinidad de zumbadores en la mochila.
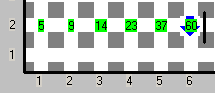
5) Al final, en cada celda del segundo renglón que esté entre la (2,2) y la pared debe tener los términos de sucesión de Fibonnacci.
6) Karel debe terminar sobre el último término de la sucesión.
Ejemplo
| entrada | salida |
 |
 |
| Concurso: | 11a OMI, Aguascalientes - Examen Final. 1/Abril/2006 |
| Propuesto por: | Pier Paolo Guillén Hernández |
| Ayuda: | mundos, condiciones, sugerencias |
| Soluciones: | fibo.txt (pascal), fibo.txt (java) |