A manera de ejemplo y para englobar parte de los conceptos presentados en este capítulo, consideremos el siguiente código:


Este código corresponde al algoritmo de ordenación por burbuja. La finalidad de este algoritmo es ordenar un arreglo de menor a mayor. La entrada del algoritmo es el arreglo a que vamos a ordenar y la cantidad n de casillas con que cuenta. La salida consiste en el arreglo ordenado. En lo que se basa este algoritmo es en que si dos casillas continuas están desordenadas (la primera es mayor a la segunda), entonces las volteamos. Repetimos esto hasta que todas las casillas estén ordenadas.

Vamos a calcular las cotas para este algoritmo. Vemos que tiene dos ciclos anidados (el repeat de la línea 4 y el for de la línea 7), así que podemos tomar una estimación para la cota superior de O(n²). Ya con esto sabemos que el problema de ordenación se encuentra en P y por lo tanto es un problema fácil.

Para los siguientes cálculos supondremos que el costo de cada operación es de 1, además de que no consideraremos a begin, end ni repeat como operaciones.

El mejor caso se cumpliría cuando el arreglo a ordenar en realidad no lo necesitara, con lo que la instrucciones 5 y 13 se ejecutarían 1 vez, y las 6 y 7 se ejecutarían n-1 veces por lo que su función sería f(n) = 2(n-1) + 2 = 2n, con lo que tendríamos una complejidad de Ω(n).

El peor caso sucede si se nos presenta que el arreglo esté ordenado de mayor a menor. Como en cada iteración del repeat el menor número desciende sólo una casilla, se necesitan n repeticiones para que llegue a su posición correcta. En este caso las líneas 5 y 13 se ejecutan n veces, las 6 y 7 n(n-1) veces, y de la 9 a la 11 se ejecutan 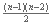veces. Con esto tenemos que la función del peor caso es f(n) = 2n + 2n(n-1) + 3 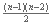= 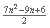, por lo que tendríamos una cota O(n²).

Para el caso promedio, la probabilidad de que se ejecuten las líneas 5 y 13 está distribuida uniformemente por lo que esperamos que sean 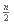veces. Con esto sabemos que las líneas 6 y 7 se ejecutarían 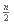(n-1) veces, y esperaríamos que las líneas 9, 10 y 11 corrieran en 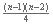ocasiones. Por lo tanto, la función para el caso promedio es f(n) = 2(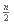) + 2(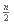)(n-1) + 3 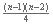= 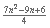, esto es Θ(n²).