A pesar de que el peor caso de este algoritmo es O(n²), es uno de los más empleados. Esto se debe a que su implementación es compacta, por lo que las constantes del tiempo de ejecución son muy bajas. Además, su peor caso ocurre muy pocas veces en aplicaciones de propósito general.

Este algoritmo utiliza la técnica “Divide y Vencerás” (sección 11.7) para ordenar los datos. Lo que hacemos es escoger un elemento en la lista, al cual llamaremos pivote, y ordenamos los datos en dos subarreglos, dejando los datos que son mayores a este elemento en uno y los menores en el otro. Una vez que hayamos hecho esto, aplicamos el mismo procedimiento en los subarreglos, y repetimos este procedimiento hasta que todos los datos se encuentren ordenados.

El peor caso de esta ordenación ocurre cuando en cada recursión, el pivote queda como único elemento de un subarreglo. Si esto sucede, tomaríamos todos los elementos de la lista como pivotes en algún momento, y cada que hiciéramos esto, recorreríamos todo el arreglo creando los subarreglos, por lo que tenemos la cota de O(n²).

Tomando como pivote el primer dato, el peor caso se presenta únicamente cuando el arreglo ya está ordenado, ya sea en forma no decreciente o no creciente. Para minimizar esto, hay versiones de la ordenación rápida que permutan aleatoriamente la entrada antes de ordenarla, por lo que ninguna entrada en especial ocasiona el peor caso (aunque todavía puede ocurrir).

La mejor elección del pivote es la mediana del vector, pero encontrarla implica un tiempo extra que vuelve al algoritmo ineficiente. Si conocemos la naturaleza de los datos a ordenar, podemos escoger los datos de acuerdo a esto. Como generalmente no la conocemos, podemos tomar cualquier elemento como pivote. Otra implementación común es tomar tres elementos aleatorios y utilizar como pivote la mediana de estos tres.

Una mejora mas que se puede aplicar al algoritmo es utilizar otro método para ordenar los subarreglos una vez que sean de tamaño pequeño. Por ejemplo, si los subarreglos son de tamaño menor a 10 podríamos mandarlos a ordenar mediante inserción. El valor de 10 es meramente demostrativo, y en la práctica lo podríamos obtener afinando a prueba y error.




Solución: El algoritmo para obtener el valor de cada nombre es simple, sólo que necesitamos tener los nombres en orden. Aunque lo podemos ordenar con casi cualquier método, escogemos Quicksort ya que la entrada es relativamente grande (5000 nombres).




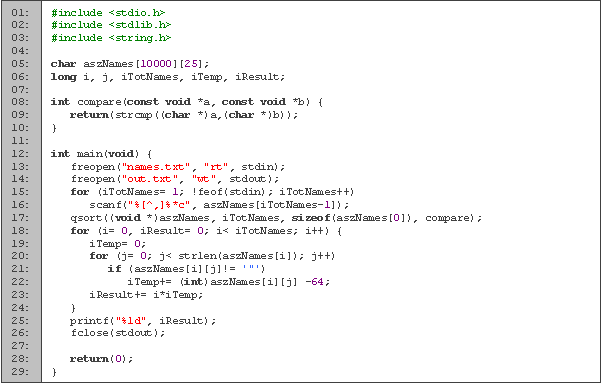
Empezamos declarando en las primeras cuatro líneas las variables a utilizar. La lectura de los nombres la haremos caracter por caracter mediante ch, y guardamos los nombres en el arreglo a. Para los ciclos empleamos i y j, n para el total de datos, t es una variable temporal, y en r guardamos el resultado.

Enseguida tenemos la función quicksort, que ordena un arreglo entre las casillas l y r. Las variables i y j son para recorrer el arreglo, x es el pivote y t es una variable temporal. En las líneas 10 y 11 inicializamos las variables. Entre la 13 y la 14 recorremos el arreglo buscando elementos que no estén acomodadas con respecto al pivote. Una vez que los encontremos, los cambiamos de lugar y continuamos el proceso. Esto lo repetimos hasta que las variables con las que recorremos el arreglo se crucen. Terminamos revisando la posición de las variables y mandando a ordenar los subarreglos en caso que sea necesario.

Algo importante es que el pivote lo escogimos como la casilla media del arreglo (que no es la mediana del arreglo), por lo que el peor caso no se daría cuando estuvieran ordenados los datos, sino con entradas en las que el menor o el mayor elemento se encontraran siempre a la mitad del subarreglo.

Al final, tenemos entre las líneas 25 y 51 la parte principal de código. Para manejar los archivos de entrada y salida, en línea 26 asignamos el archivo names.txt como el de entrada, en la 27 out.txt como el de salida, y en la 50 cerramos el archivo de salida. El archivo de entrada no es necesario cerrarlo (aunque podemos hacerlo), pero si no cerramos el archivo de salida, es posible que no se escriban todos los datos.

Entre las líneas 28 y 39 leemos los nombres. Primero inicializamos el total a cero (línea 28) y mientras no se termine el archivo seguimos leyendo. Cada que vamos a leer otro nombre, incrementamos el total y limpiamos cadena donde lo guardaremos (líneas 31 y 32). Cada nombre lo leemos hasta llegar a una coma, excepto el último que es hasta el fin de archivo. En la línea 36 omitimos las comillas, ya que no las necesitamos.

Mandamos ordenar los datos, e inicializamos el resultado. Por cada nombre, sumamos cada una de las letras (líneas 45 y 46) e incrementamos el resultado por el producto de la suma y la posición del nombre. En la línea 46 restamos 64 ya que ord nos devuelve el valor ASCII del caracter. Terminamos imprimiendo la respuesta en la línea 49.

Entrada:	"MARY","PATRICIA","LINDA","BARBARA","ELIZABETH","JENNIFER", "MARIA","SUSAN"
Desarrollo:	MARY PATRICIA LINDA BARBARA ELIZABETH JENNIFER MARIA SUSAN MARY PATRICIA LINDA BARBARA ELIZABETH JENNIFER MARIA SUSAN BARBARA PATRICIA LINDA MARY ELIZABETH JENNIFER MARIA SUSAN         PATRICIA LINDA MARY ELIZABETH JENNIFER MARIA SUSAN         ELIZABETH LINDA MARY PATRICIA JENNIFER MARIA SUSAN                   LINDA MARY PATRICIA JENNIFER MARIA SUSAN                   LINDA MARY MARIA JENNIFER PATRICIA SUSAN                   LINDA MARY MARIA JENNIFER                   LINDA JENNIFER MARIA MARY                   LINDA JENNIFER MARIA                   JENNIFER LINDA MARIA                            LINDA MARIA                                             PATRICIA SUSAN BARBARA ELIZABETH JENNIFER LINDA MARIA MARY PATRICIA SUSAN i  t   r 1  43  43 2  88  219 3  81  462 4  40  622 5  42  832 6  57  1174 7  77  1713 8  74  2305
Salida:	2305