La ordenación por montículos toma su nombre de las estructuras conocidas como montículos, que son una clase especial de árboles (sección 9.1). Este tipo de árboles poseen la característica de que son binarios completos, lo que significa que cada vértice tiene a los más dos hijos, y que todos sus niveles están completos, excepto (posiblemente) el último, el cuál se llena de izquierda a derecha. Otra particularidad que deben cumplir es que todo vértice debe ser igual o mayor a cualquiera de sus hijos. En consecuencia, el elemento mayor siempre los podemos encontrar en la raíz.
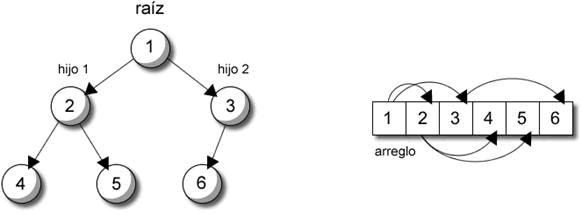 |
| Figura 3.1: Representación en árbol y en arreglo de un montículo. |
La ordenación por montículos utiliza la propiedad de la raíz para ordenar el arreglo. Una vez que el arreglo cumpla las propiedades del montículo, quitamos la raíz y la colocamos al final del arreglo. Con los datos que sobran, creamos otro montículo y repetimos hasta que todos los datos estén ordenados.
Se da una serie de n enteros no negativos. Definamos a la mediana de dicha serie. Si n es un número impar, la mediana es el elemento que se encuentra a la mitad de la serie una vez que ésta es ordenada. Puedes darte cuenta que en este caso la mediana es elemento de posición en la serie ordenada, si empezamos a contar desde 1. Si n es par, la mediana se obtiene mediante la semi-suma de los dos elementos que se encuentran en medio de la serie ordenada. Esto es, es la semi-suma de los elementos con posiciones
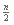 y
y 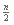 +1 de la serie ordenada. Ten en cuenta que la serie no necesariamente está ordenada.
+1 de la serie ordenada. Ten en cuenta que la serie no necesariamente está ordenada.Solución: Encontrar la mediana en un arreglo ordenado no es complicado, pero las limitantes en memoria del problema (1MB) nos impiden guardar el arreglo completo. Una solución es guardar únicamente uno más de la mitad de los datos y cada que leamos uno nuevo, si es menor al más grande del arreglo, sacamos el mayor y guardamos el que leímos.
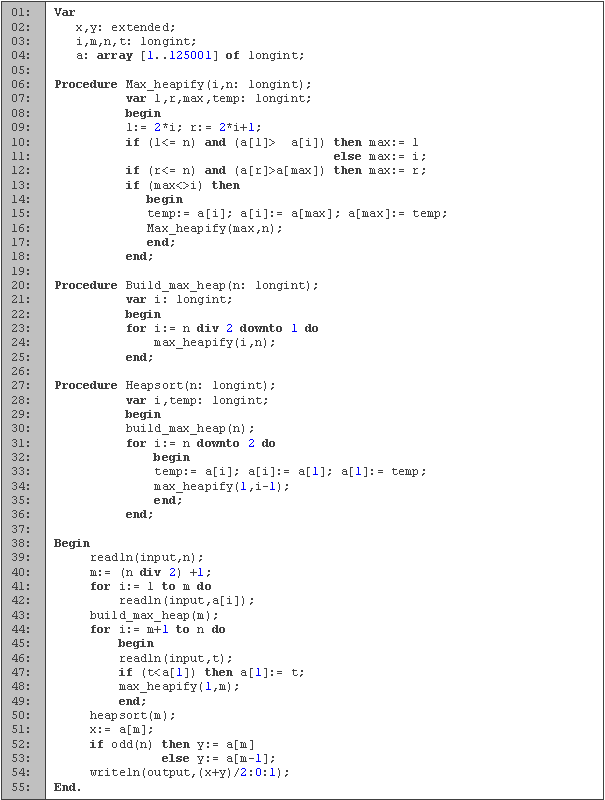
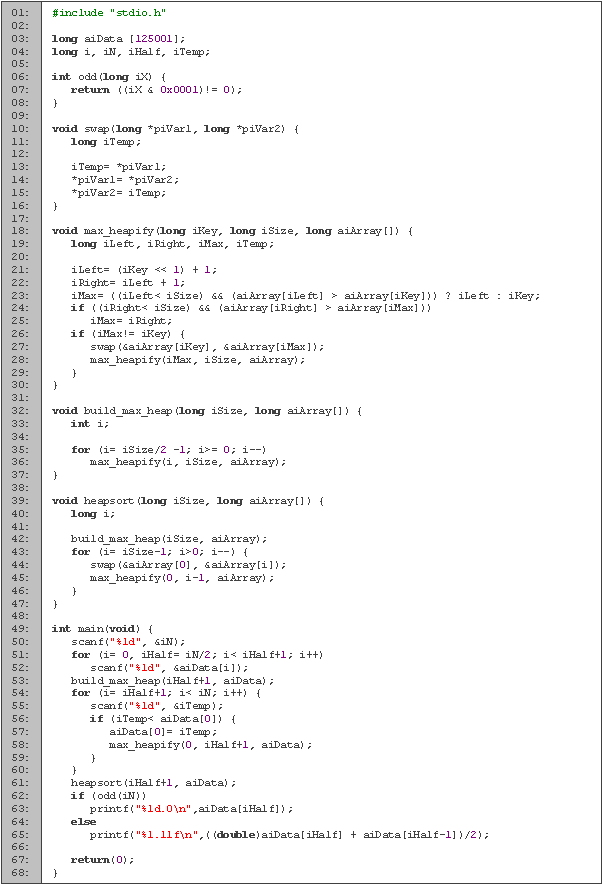
De la línea 1 a la 4 definimos las variables a emplear. El entero i lo utilizamos para los ciclos, n es el total de datos, m es la mitad más uno y t es un entero temporal. En el arreglo a guardamos los datos a utilizar, y las variables x e y son temporales que utilizamos para calcular la mediana ya que el tamaño de los datos puede exceder la capacidad de un longint.
La función max_heapify (líneas 6 a 18) se encarga de hacer que un elemento i en un arreglo de tamaño n cumpla la condición de los vértices, esto es, que el padre sea mayor que los hijos. En la línea 9 obtenemos cuales son los hijos del vértice. Es fácil notar que el hijo izquierdo de un vértice en la posición i es el que se encuentra en la posición 2i y el hijo derecho es el que le sigue. En las líneas 10 a 12 encontramos cual de estas casillas contiene el mayor elemento. Si el mayor elemento no es el padre, entonces intercambiamos el padre con el mayor elemento (línea 15), cumpliéndose así la condición del montículo. Revisamos recursivamente si el elemento que cambiamos cumple con la propiedad del montículo en su nueva posición (línea 16).
Después contamos con la función build_max_heap (líneas 20 a 25) la cual crea un montículo dentro del arreglo. Lo primero que debemos notar es que podemos crear el montículo utilizando el procedimiento max_heapify del último elemento al primero. Esto es porque al utilizar el i-ésimo elemento, sabemos que todos los demás elementos que ramifican de él ya cumplen con las propiedades del montículo, excepto (posiblemente) i. Otra cosa que podemos notar es que los datos que están en el último nivel (desde i+1 hasta n), no tienen hijos, por lo que podemos ignorarlos.
Los datos los ordenamos a través de la función heapsort (líneas 27 a 36). Empezamos creando el montículo en la línea 30. El mayor elemento (la raíz), lo mandamos a su posición ordenada (línea 33). Al intercambiar las casillas, tenemos que hacer que los datos restantes sigan cumpliendo las propiedades del montículo. Como el único elemento que no cumple es el que acabamos de cambiar, utilizamos max_heapify en esta casilla. Así, en cada iteración, los últimos datos ya están ordenados.
La parte principal del código está entre las líneas 38 y 55. Empezamos leyendo la cantidad de datos en n (línea 39) y leemos la primera mitad más uno de los datos (líneas 40 a 42). Teniendo estos datos, construimos el montículo (línea 43). Para los siguientes datos, cada que leemos uno, revisamos si es más chico que la raíz (línea 47), y de ser así, los cambiamos y acomodamos el elemento que acabamos de agregar. Con esto nos aseguramos que en el arreglo contamos con los m elementos menores. Una vez que tenemos ordenados los datos (línea 50), la mediana la encontramos en la posición m si la cantidad de datos es impar o en el promedio de la m y la m-1 si es par. Utilizamos variables extended para evitar que los datos se desborden al realizar la suma (podemos utilizar cualquier otra variable mayor a longint, como int64).Una mejora que podemos hacer es no construir el montículo al inicio de la ordenación (línea 30), ya que sabemos que el arreglo ya contiene un montículo (por las líneas 43 y 48). Observando más a detalle, podemos quitar completamente el ordenamiento notando que antes de ordenar los datos, la mediana se encuentra en primera casilla si la cantidad de datos es impar, y en el promedio entre la primera y la segunda o la tercera si la cantidad de datos es par.
| Entrada: | 10 7 38 3 29 16 15 28 42 27 43 |
| Desarrollo: | 7 38 3 29 16 15 7 38 3 29 16 15 7 38 15 29 16 3 7 38 15 29 16 3 7 38 15 29 16 3 38 7 15 29 16 3 38 29 15 7 16 3 28 < 38 28 29 15 7 16 3 29 28 15 7 16 3 42 > 29 27 < 29 27 28 15 7 16 3 28 27 15 7 16 3 43 > 28 28 27 15 7 16 3 3 27 15 7 16 28 27 3 15 7 16 27 16 15 6 3 3 16 15 6 27 28 16 3 15 6 16 6 15 3 3 6 15 16 27 28 15 6 3 3 6 15 16 27 28 6 3 3 6 15 16 27 28 3 6 15 16 27 28 (28 + 27)/2 = 27.5 |
| Salida: | 27.5 |
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 19-Feb-2006 | 0.218 | 0.031 | 0.234 | 0.968 | 614 |
| C | 17-Mar-2006 | 0.140 | 658 | |||
 Ordenación Rápida de Hoare (Quicksort)
Ordenación Rápida de Hoare (Quicksort)
