El ordenamiento por conteo tiene la particularidad de que en ningún momento necesitamos realizar comparaciones entre los números, por lo que la cota mínima de O(nlgn) no aplica.
Este método tiene la restricción de que sólo puede ser aplicado en elementos en un intervalo de a lo más k elementos, típicamente en números naturales en el rango de 1 a k. Su cota de tiempo es de O(n + k), por lo que para ser mejor que el ordenamiento a base de comparaciones, se debe cumplir que k < nlgn. Por esto, este algoritmo es útil principalmente cuando contamos con muchos datos en un rango corto.
Para ordenar un arreglo mediante este método, contamos en un arreglo auxiliar cuantas veces se encuentra cada número en el arreglo original. Una vez que tengamos las veces que aparecen, podemos saber cuantos números son menores sumando las casillas anteriores. Ahora que conocemos la cantidad de datos que son menores, podemos acomodar el dato en la casilla que le corresponde.
Según la implementación, este algoritmo puede ser estable. Siendo así, se puede usar como paso intermedio en una ordenación conocida como ordenación Radix.(Radixsort). Esta ordenación sirve principalmente para ordenar números, y utilizamos una k equivalente a la base en la que trabajemos. Después ordenamos los números considerando un dígito a la vez, del menos al más significativo. En base 10, ordenaríamos primero usando las unidades, luego decenas, centenas, y así sucesivamente.
Problema ejemplo
Preguntas y Respuestas
La base de datos del Pentágono contiene información clasificada como secreta. No sabemos en que consiste esta información - ya que es secreta, - pero sabemos en que formato se encuentra representada. Es extremadamente simple. No sabemos porque, pero todos los datos están codificados en números naturales entre 1 y 5000. El tamaño de la base de datos central (que nombraremos n) es relativamente grande - puede contener hasta 100 000 de estos números. La base de datos debe procesar la información rápidamente. La solicitud más frecuente es: "¿Cuál elemento se encuentra en la i-ésima posición?" - donde i es un número natural que se encuentra entre 1 y n.
Problema
Debes hacer un programa que pueda servir de controlador de la base de datos. En otras palabras, debe poder procesar rápidamente solicitudes como ésta.Entrada
La entrada de este problema consiste de dos partes. Primero, se ingresa una base de datos y después una serie de solicitudes. El formato de la base de datos es muy simple: en la primera línea se incluye un número n, en las siguientes n líneas existen n números ordenados aleatoriamente. La serie de solicitudes también tiene un formato simple: la primera línea es la cantidad de solicitudes k (1 ≤ k ≤ 100), seguido por k líneas que contienen una solicitud cada una. La solicitud "¿Cuál elemento se encuentra en la i-ésima posición?" está representada por el número i. La base de datos se encuentra separada de la serie de solicitudes por una cadena que contiene tres veces el símbolo "#".Salida
La salida debe contener k líneas. En cada línea debe estar la respuesta a la solicitud. La respuesta para la solicitud "i" es un elemento perteneciente a la base de datos, que está en la posición i-ésima (ordenando los datos de menor a mayor).
Solución: Teniendo los datos ordenados, obtener el i-ésimo dato es sencillo. Como la cantidad de datos es grande (100 000) pero el rango no (1 a 5000), el ordenamiento por conteo es buena opción.
Código
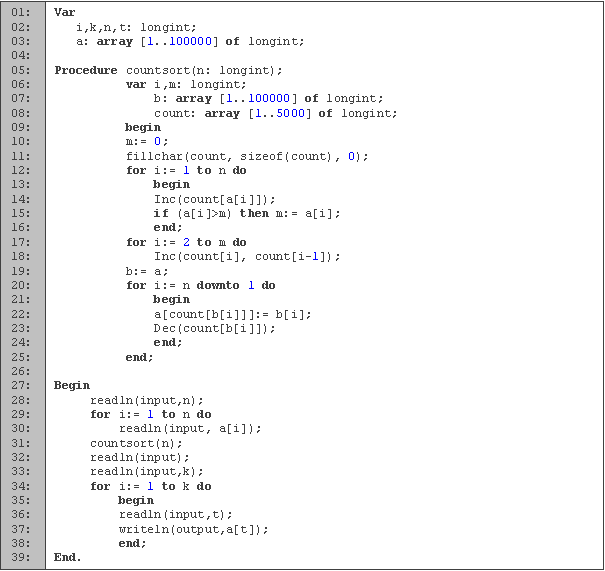
Las primeras tres líneas son donde declaramos las variable que utilizaremos. Para los ciclos usaremos i, n para la cantidad de datos en el arreglo y k para la cantidad de datos por buscar. En t leemos la posición del dato a buscar y a es el arreglo a ordenar.
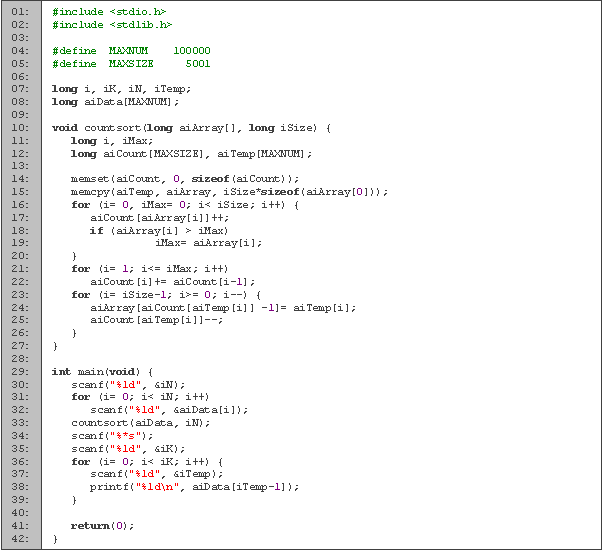
De la línea 5 a la 25 tenemos la función countsort que es la que efectúa la ordenación por conteo. La variable i nos va a servir en los ciclos, en m guardamos el número máximo, count y b son arreglos auxiliares. Entre las líneas 10 y 16 contamos la aparición de cada número, y guardamos al mayor en m. El siguiente par de líneas (17 y 18), incrementa cada casilla de count en el valor anterior, por lo que al final tendremos en cada casilla cuantos números son menores o iguales.
Copiamos el arreglo original a en b. Por cada dato que tenemos en el arreglo, vemos en cuantos datos existen que son menores o iguales, y lo colocamos en esa posición. Como pueden existir varios datos con el mismo valor, cada vez que insertamos un dato, decrementamos la cantidad de datos que son menores o iguales. Recorremos el arreglo en reversa para asegurar que el ordenamiento sea estable.
Caso ejemplo
| Entrada: | 10 5 1 4 9 7 9 6 4 9 8 ### 4 3 3 2 5 |
| Desarrollo: | 1 2 3 4 5 6 7 8 9 count 1 0 0 2 1 1 1 1 3 (cuenta de cada uno) count 1 1 1 3 4 5 6 7 10 (acumulado) b a count 8, count[8]= 7 x x x x x x 8 x x x 1 1 1 3 4 5 6 6 10 9, count[9]= 10 x x x x x x 8 x x 9 1 1 1 3 4 5 6 6 9 4, count[4]= 3 x x 4 x x x 8 x x 9 1 1 1 2 4 5 6 6 9 6, count[6]= 5 x x 4 x 6 x 8 x x 9 1 1 1 2 4 4 6 6 9 9, count[9]= 9 x x 4 x 6 x 8 x 9 9 1 1 1 2 4 4 6 6 8 7, count[7]= 6 x x 4 x 6 7 8 x 9 9 1 1 1 2 4 4 5 6 8 9, count[9]= 8 x x 4 x 6 7 8 9 9 9 1 1 1 2 4 4 5 6 7 4, count[4]= 2 x 4 4 x 6 7 8 9 9 9 1 1 1 1 4 4 5 6 7 1, count[1]= 1 1 4 4 x 6 7 8 9 9 9 0 1 1 1 4 4 5 6 7 5, count[5]= 4 1 4 4 5 6 7 8 9 9 9 0 1 1 1 3 4 5 6 7 |
| Salida: | 4 4 4 6 |
Código en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 28-Feb-2006 | 0.031 | 0.001 | 0.062 | 1.942 | 946 |
| C | 28-Feb-2006 | 0.031 | 946 | |||
Ordenación por montículos (Heapsort)
