Esta búsqueda es directa y se basa en el uso de “fuerza bruta”. Si el dato que necesitamos buscar se encuentra dentro del arreglo, buscando en todas las casillas lo debemos encontrar. Para hacerlo de una manera organizada, empezamos por el primer dato y continuamos hasta llegar al dato que buscamos o hasta que lleguemos al fin del arreglo.
Un algoritmo tan simple puede parecer inútil, pero si no queremos ordenar los datos (o no hay forma de hacerlo) es la única opción que tenemos. En general, ordenar los datos nos tomaría O(nlgn) y buscarlos eficientemente O(lgn), por lo que si necesitamos buscar pocas veces algún valor, no es conveniente.
Problema ejemplo
Posiciones Finales
El viejo sistema utilizado en los concursos utilizaba una ordenación por burbuja para generar los resultados finales. Pero ahora participan demasiados equipos y el programa trabaja demasiado lento.
Problema
Se te pide escribir un programa que genere exactamente la misma salida que el programa original, pero rápidamente..Entrada
La primera línea de la entrada contiene solamente un entero 1 < n < 150000 - la cantidad de equipos. Las siguientes n líneas contienen dos enteros 1 ≤ ID ≤ 10000000 y 0 ≤ m ≤ 100. ID - número único que identifica a cada equipo, m - cantidad de problemas resueltos.Salida
La salida debe contener n líneas con dos enteros, ID y m, cada una. Las líneas deben estar ordenadas por el valor de m en orden descendiente como si hubieran sido ordenadas mediante burbuja (o algún método análogo).
Solución: Nos afirman que la ordenación por burbuja es demasiado lenta (lo cual podemos comprobar fácilmente), y que debemos encontrar una alternativa. Cualquier otro algoritmo O(n2) será igual de ineficiente, por lo que debemos buscar uno con cota menor.
Un problema con el que nos enfrentamos es que la ordenación por burbuja es estable, por lo que el algoritmo que lo reemplaza también debe ser estable. Ordenación por Inserción cumple este requisito, pero tiene la misma complejidad que la ordenación por Burbuja. Podríamos ordenarlos por Mezcla o por Conteo, pero estos métodos requieren demasiada memoria (más de la que disponemos).
Es posible modificar la ordenación Rápida de Hoare para que sea estable, pero existe una solución más simple. Guardamos todos los datos, y en lugar de ordenarlos, buscamos primero los equipos que resolvieron más problemas, luego los que resolvieron uno menos, y así sucesivamente hasta que lleguemos a los que no resolvieron problema alguno.
Código

En las primeras tres líneas declaramos las variables globales que vamos a utilizar. En n leemos la cantidad de datos a utilizar, en m leemos el número de problemas resueltos, t sirve para encontrar la cantidad máxima de problemas resueltos, i es una variable para ciclos, y en d guardamos tanto el número de equipos como la cantidad de problemas que resolvió.
Una de nuestras principales limitantes es la memoria, por lo que vamos a realizar un pequeño “truco” para eficientar espacio. Normalmente utilizaríamos un arreglo de longint (4 bytes) para los números de los equipos y uno de shortint (1 byte) para los problemas resueltos. Con esto, el espacio que necesitaríamos por cada equipo es de 5 bytes. El número de identificación máximo que puede tener un equipo es de 10 millones, que necesita menos de 3 bytes. Por esto, podemos guardar los problemas en el primer byte y el número en los siguientes tres, todo dentro del longint. Con esto tenemos un ahorro del 20% en memoria.
Ya sabemos como ahorrar memoria, pero también necesitamos saber como implementarlo. Conocemos que un byte es equivalente a ocho bits, por lo que desplazando el número de equipo ocho veces a la izquierda (los desplazamiento se explican más a fondo en la sección 6.5), ahora el número iniciaría a partir del segundo byte. Para regresar el número a como estaba originalmente lo hacemos mediante ocho desplazamientos a la derecha.
 |
| Figura 3.2: Desplazamientos de 1 byte (8 bits) a la izquierda y derecha. |
Para poder meter la cantidad de problemas en el primer byte, lo hacemos mediante la operación OR entre el número en el que lo queremos guardar (d[i]) y el número que queremos guardar (m). Si queremos volver a leer el número de problemas, lo hacemos mediante la operación AND entre el número y FF (8 unos en el primer byte).
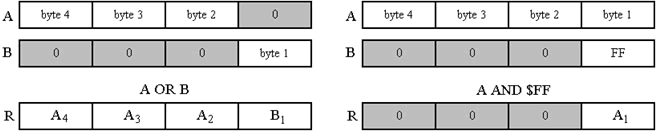 |
| Figura 3.3: Inserción de bytes mediante OR y selección de bytes mediante AND. |
Entre las líneas 5 y 11 se encuentra el procedimiento de la búsqueda lineal (busqlineal). Empezamos declarando en la línea 6 la variable i que nos va a servir para recorrer el arreglo. Entre las líneas 8 y 10 buscamos el número, y en caso de encontrarlo lo imprimimos. Normalmente, la búsqueda la realizaríamos hasta el primer dato que fuera igual a x y devolveríamos la posición en la que lo encontramos o alguna notificación en caso contrario.
Por último, buscamos linealmente los equipos que resolvieron la mayor cantidad, después los que resolvieron uno menos, y seguimos realizándolo hasta que lleguemos a los que no resolvieron problemas.
Caso ejemplo
| Entrada: | 8 1 2 16 3 11 2 20 3 3 5 26 4 7 1 22 4 |
| Desarrollo: | ( 1 shl 8) OR 2 = 258 (16 shl 8) OR 3 = 4099 (11 shl 8) OR 2 = 2818 (20 shl 8) OR 3 = 5123 ( 3 shl 8) OR 5 = 773 (26 shl 8) OR 4 = 6660 ( 7 shl 8) OR 1 = 1793 (22 shl 8) OR 4 = 5636 búsqueda 5 258, 4099, 2818, 5123, 773, 6660, 1793, 5636 4 258, 4099, 2818, 5123, 773, 6660, 1793, 5636 3 258, 4099, 2818, 5123, 773, 6660, 1793, 5636 2 258, 4099, 2818, 5123, 773, 6660, 1793, 5636 1 258, 4099, 2818, 5123, 773, 6660, 1793, 5636 0 258, 4099, 2818, 5123, 773, 6660, 1793, 5636 |
| Salida: | 3 5 26 4 22 4 16 3 20 3 1 2 11 2 7 1 |
Código en C

Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 28-Feb-2006 | 0.296 | 0.078 | 0.420 | 1.000 | 710 |
| C | 28-Feb-2006 | 0.265 | 718 | |||
 Ordenación por conteo (Countingsort)
Ordenación por conteo (Countingsort)
