El estudio de los números primos pertenece a la teoría de números. En este capítulo vamos a tratar a los números primos como parte de los números naturales, ya que es como más comúnmente se presentan en los problemas. Sin embargo, se pueden incluir más ampliamente en los números enteros con algunas consideraciones sobre los signos.

Los números naturales constituyen el subconjunto de los números enteros que son positivos, o el subconjunto de los no negativos, de acuerdo con el autor. Estos es, puede ser el conjunto {1, 2, 3, ...} o el conjunto {0, 1, 2, ...}. Comúnmente, en teoría de números no se incluye el cero, mientras en teoría de conjuntos, lógica e informática sí se le considera. Dentro de los concursos de programación se pueden encontrar las dos variantes.

Un número primo es aquel que solamente tiene un divisor propio, esto quiere decir que el único número menor a si mismo que lo puede dividir sin dejar residuo es el uno. A los números que no son primos, excluyendo al uno, se les llama compuestos. El número uno no es ni primo ni compuesto y se le conoce como unidad. El cero normalmente no entra en ninguna de estas categorías, aunque en ocasiones se le considera compuesto.

Los primos se pueden ver como los constructores de los demás números: todo número natural distinto de uno puede ser escrito de forma única, salvo permutaciones, como producto de números primos. A este enunciado se le conoce como el Teorema Fundamental de la Aritmética.

Los primos gozan de gran popularidad en las matemáticas desde el tiempo de los griegos clásicos. Euclides demostró que la cantidad de números primos es infinita, y los matemáticos siempre han estado interesados en encontrar números primos grandes. El primo más grande conocido hasta ahora fue encontrado el 23 de Agosto de 2008 a través del proyecto colaborativo GIMPS (Great Internet Mersenne Prime Search) y corresponde a un primo de Mersenne, los cuales provienen de la forma 2ⁿ -1. Para el primo que rompió el record, n = 43 112 609 y contiene 12 978 189 dígitos.

Existen varías conjeturas relacionadas con los números primos que atraen el interés de investigadores. Golbach conjeturó que cada número natural par puede descomponerse en una suma de dos números primos. Se cree que todo número impar mayor que cinco se puede descomponer como la suma de tres números primos. Otra conjetura no demostrada es que la cantidad de primos gemelos (primos cuya diferencia sea de dos) es infinita.

Inclusive existen intentos por encontrar fórmulas que siempre generen números primos, siendo las más famosas n² + n + 41 propuesta por Euler (deja de funcionar cuando n = 40) y 2²ⁿ + 1 propuesta por Fermat (deja de funcionar para n = 5). Hasta ahora no se ha podido encontrar una fórmula que siempre funcione, como tampoco se ha demostrado que tal fórmula no existe.

Otro tema que ha despertado el interés de los estudiosos es cómo están distribuidos todos los números primos. Se define P(n) como la función que nos indica cuantos primos hay en el intervalo de uno a n. Legendre y Gauss notaron que mientras más crecía n, la relación 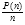tiende a 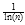. En 1896, Charles de la Vallée-Poussin y Jacques Hadamard demostraron de forma independiente este teorema.

Se le puede sacar provecho a las dificultades que presenta el cálculo de los números primos. Estos números y la matemática modular son pieza clave en la criptografía moderna. La mayoría de las encriptaciones modernas se basan en propiedades de estos números, ya que hasta el momento no se conoce forma de descifrar sus códigos (sin conocer la clave).