Teniendo los números enteros a y b, a es divisor de b si se cumple que a divide a b sin dejar residuo, esto quiere decir que existe un número entero k tal que b = ka y que b ≡ 0 mod a. Si a es divisor de b se representa simbólicamente como a|b, y en caso de que no lo divida se representa como a
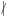b.Un número a es divisor propio de b si a divide a b sin dejar residuo y a ≠ b. Designamos a d(n) como el conjunto de los divisores propios de n y a s(n) como la suma de todos estos divisores. Por ejemplo:
| d(5) = {1} | s(5) = 1 |
| d(12) = {1,2,3,4,6} | s(12) = 1 + 2 + 3 + 4 + 6 = 16 |
Problema ejemplo
Perfección
Problema
Del artículo Teoría de Números de la Enciclopedia Microsoft Encarta de 1994: “Si a, b y c son enteros tales que a = bc, a a se le conoce como múltiplo de b o c, y b o c se le llama divisor o factor de a. En el caso de que c no sea 1 o -1, a b se le llama divisor propio de a. Los números pares, incluyendo al 0, todos son múltiplos de 2, por ejemplo, -4, 0, 2, 10; los números impares (nones) son los enteros que no son pares, por ejemplo, -5, 1, 3, 9. Un número perfecto es un entero positivo que es igual a la suma de todos sus divisores propios positivos; por ejemplo, 6, que es igual a 1 + 2 + 3, y 28, que es igual a 1 + 2 + 4 + 7 + 14, son números perfectos. Un número es imperfecto en caso de no ser perfecto, y puede ser deficiente o abundante de acuerdo a si la suma de los divisores propios es menor o mayor al número mismo. Por lo tanto, 9, con divisores 1 y 3, es deficiente; 12, con divisores propios 1, 2, 3, 4 y 6 es abundante.Dado un número, determinar si es perfecto, abundante o deficiente.
Entrada
Una lista de n enteros positivos (ninguno mayor a 60 000), con 1 < n < 100. Un 0 marcará el final de la listaSalida
La primera línea de salida debe decir PERFECTION OUTPUT. Las siguientes n líneas de salida deberán ser una lista que indique para cada entero si es perfecto (PERFECT), deficiente (DEFICIENT) o abundante (ABUNDANT). El formato es importante: los enteros de la salida deben estar justificados a 5 espacios, seguido por dos espacios en blanco, y por la descripción del entero. La línea final de la salida debe ser END OF OUTPUT.Solución: Si n tiene algún divisor entonces los podemos representar como n = ab, y alguno de sus dos divisores tiene que ser menor o igual que la raíz de n, ya que si los dos fueran mas grandes que la raíz su producto sería (
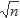+ d)(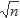 + e), donde d y e son positivos, el cual es claramente mayor a n.Por lo anterior hacemos un recorrido hasta la raíz de n, si encontramos un número a que divida a n lo sumamos al total y también añadimos a b (que sería
). El único problema es que cuando n tiene raíz exacta, a = b y estaríamos contando dos veces un divisor, por lo que hacemos una revisión al final.Código
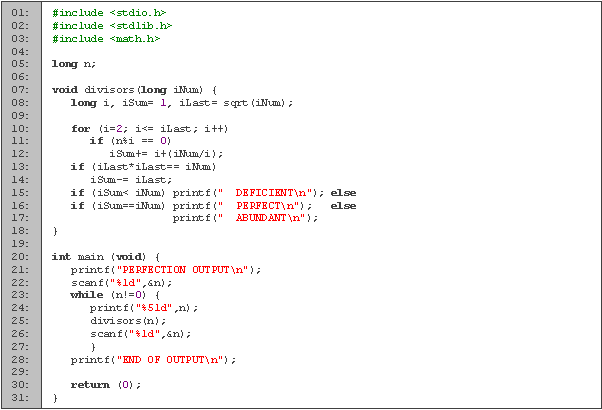
Iniciamos declarando sólo una variable: n, que es el número a revisar (líneas 1 y 2).
En las líneas 4 a 14 tenemos la función divisores que es precisamente donde vamos a ver cuantos divisores tiene el número. Declaramos en la línea 5 las variables locales: i es una variable de ciclo y s es la suma de todos los divisores. Inicializamos la suma a uno (línea 7) y en las líneas 8 y 9 vamos agregando los divisores a la suma. En la línea 10 revisamos si el número es un cuadrado, y en caso de que lo sea, le quitamos el divisor que sumamos de más. Terminamos poniendo si el número es deficiente, perfecto o abundante, según si la suma es menor, igual o mayor que n.
Información adicional
Euclides demostró que la fórmula 2n-1(2n -1) siempre da como resultado un número perfecto cuando 2n -1 es un número primo. Tiempo después, Euler demostró que tal fórmula sirve para encontrar todos los números perfectos pares. Hasta la fecha no se han encontrado números perfectos impares y se cree que no existen, aunque no ha sido demostrado.
Casos ejemplo
| Entrada: | 81 |
| Desarrollo: | s = 1 81 ≡ 1 mod 2 81 ≡ 0 mod 3, s = 1 + 3 + 27 = 31 81 ≡ 1 mod 4 81 ≡ 1 mod 5 81 ≡ 3 mod 6 81 ≡ 4 mod 7 81 ≡ 1 mod 8 81 ≡ 0 mod 9, s = 31 + 9 + 9 = 49 92 = 81, s = 49 –9 = 40 40 < 81 |
| Salida: | 81 DEFICIENT |
| Entrada: | 28 |
| Desarrollo: | s = 1 28 ≡ 0 mod 2, s = 1 + 2 + 14 = 17 28 ≡ 1 mod 3 28 ≡ 0 mod 4, s = 17 + 4 + 7 = 28 28 ≡ 3 mod 5 52 < 28 28 = 28 |
| Salida: | 28 PERFECT |
| Entrada: | 96 |
| Desarrollo: | s = 1 96 ≡ 0 mod 2, s = 1 + 2 + 48 = 51 96 ≡ 0 mod 3, s = 51 + 3 + 32 = 86 96 ≡ 0 mod 4, s = 86 + 4 + 24 = 114 96 ≡ 1 mod 5 96 ≡ 0 mod 6, s = 114 + 6 + 16 = 136 96 ≡ 2 mod 7 96 ≡ 0 mod 8, s = 136 + 8 + 12 = 156 96 ≡ 6 mod 9 92 < 96 156 > 96 |
| Salida: | 96 ABUNDANT |
Código en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 15-Ene-2006 | 0.000 | 0.000 | 0.000 | 0.940 | 308 |
| C | 16-Feb-2006 | 0.000 | 392 | |||
Otros problemas
Valladollid:
Ural:
Project Euler:
Saratov:
Sphere:
Introducción
