Dado un número natural n, queremos determinar si n es un número primo o no. Sabemos que un número es primo si sólo tiene un divisor propio. Entonces, lo primero que podemos hacer es probar con todos los números entre 2 y n-1, y si alguno divide a n entonces n no es primo.

Otra cosa que conocemos es que el único primo par es el 2, así que si n es par y distinto de dos, entones no es primo; y si es impar entonces ya sabemos que no va a ser divisible por un número par (con esto disminuimos a la mitad la búsqueda).

El último ajuste que hacemos es que si n no es primo, podemos representarlo como el producto de dos números y algunos de los dos es menor o igual que la raíz cuadrada de n (ya que si los dos números son mayores que la raíz de n, el producto será mayor que n). Por esto sólo necesitamos probar con los números impares hasta la raíz de n para saber si n es primo.




Solución: Simplemente hay que recorrer el intervalo, contar la cantidad de primos y calcular el porcentaje. Como se van a procesar varias (probablemente muchas) entradas, algo útil es primero calcular todos los valores que puede tomar n y guardar en un arreglo los resultados.




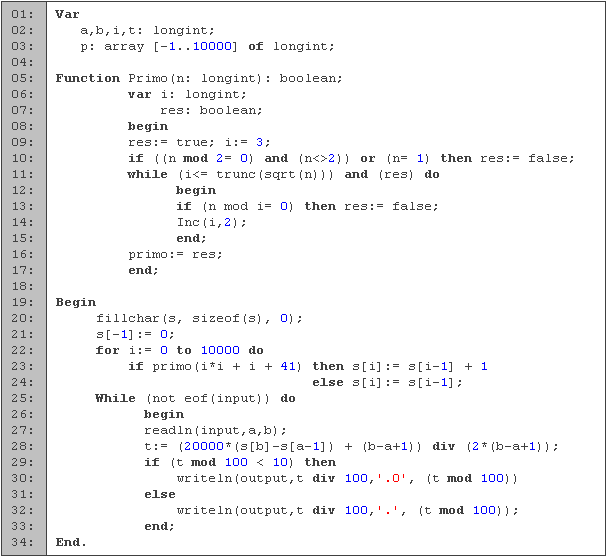
De las líneas 1 a 3 tenemos la declaración de variables: a y b determinan el intervalo a analizar, t la usamos para guardar valores temporales, i es una variable para ciclos y s es un arreglo donde guardamos cuantos primos hemos encontrado hasta n.

La función primo toma como entrada un número natural y devuelve true si el número es primo o false si es compuesto. En las líneas 6 y 7 tenemos las variables: i es una variable para ciclos y res es el resultado de la función. En la línea 9 inicializamos las variables, empezamos suponiendo que el número es primo y comenzamos a contar desde el tres. En la línea 10 quitamos los números pares y el uno, ya que sabemos que no son primos, y el único par que dejamos es el dos. Después recorremos todos los impares hasta la raíz de n, si alguno de ellos divide a n entonces es un número compuesto y nos salimos del ciclo (líneas 11 a la 15). Para terminar, en la línea 16 asignamos el resultado a la función.

De las líneas 19 a la 34 está la parte principal del programa. Primero limpiamos el arreglo s en la línea 20 (la mayoría de los compiladores inicializan a cero todas las variables globales, pero es buena costumbre programarlo de cualquier forma). En las siguientes cuatro líneas (21 a 24) guardamos cuantos primos hemos encontrado hasta el momento. El ciclo de las líneas 25 a 33 es la parte que hace lo que nos piden: leemos cual es el intervalo a evaluar (línea 27) y encontramos cuantos primos existen en el intervalo de a a b, restándole al acumulado hasta b el acumulado hasta a-1. Para evitarnos problemas con el redondeo, al encontrar el porcentaje utilizamos sólo enteros. 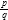Sabiendo que tenemos una fracción , el porcentaje lo obtenemos multiplicando por 100. También podemos agregar  0.005 y quitar los decimales después de los primeros dos para efectuar el redondeo. Con esto tendríamos 100(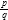)+0.005, al cual si multiplicamos por cien para tener lo que serían los decimales en los primeros dos dígitos del número, podemos reescribirlo como  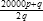(línea 28). Terminamos escribiendo el resultado entre las líneas 29 a 32.

Entrada:	151
Desarrollo:	151 ≡ 1  mod 2 151 ≡ 1  mod 3 151 ≡ 1  mod 5 151 ≡ 4  mod 7 151 ≡ 7  mod 9 151 ≡ 8  mod 11 132 > 151
Salida:	True

Entrada:	403
Desarrollo:	403 ≡ 1  mod 2 403 ≡ 1  mod 3 403 ≡ 3  mod 5 403 ≡ 4  mod 7 403 ≡ 7  mod 9 403 ≡ 7  mod 11 403 ≡ 0  mod 13
Salida:	False

Nota: Las entradas y salidas corresponden a las de la función Primo y no a las del problema.

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	13-Ene-2006	0.480	0.000	0.596	9.812	328
C	02-Feb-2006	0.290				436