La factorización es parte importante de la aritmética. El Teorema Fundamental de la Aritmética nos dice que todo número natural distinto de uno se puede escribir como producto de primos, y que esta descomposición se puede hacer de sólo una forma (exceptuando orden).

Un factor es un término equivalente a divisor. Entonces factorizar un número es lo mismo que encontrar sus divisores. Ya habíamos encontrado los divisores en la sección 4.2, pero ahora sólo queremos encontrar sus divisores primos (en específico, su descomposición canónica). Suponiendo un número natural n, su descomposición canónica sería: n = p₁^r₁p₂^r₂∙∙∙p_k^r_k, donde p₁ < p₂ < … < p_k son primos y 0 < r_i son sus potencias.

Ya teniendo la descomposición canónica, también podemos saber cuantos divisores tiene n. La forma de conocer esto es simplemente incrementar en uno todas las potencias de la descomposición y multiplicarlas.




Solución: Primero obtenemos todos los primos que vamos a necesitar (hasta la raíz de 10 000). Después recorremos de uno en uno y revisamos si dividen al número y cuántas veces lo hacen. Ya con esto sólo necesitamos incrementar en uno todos exponentes y multiplicarlos. Algo importante que debemos observar es que no necesitamos hacer la multiplicación de los diez números, ya que al multiplicar los números las potencias de la descomposición canónica se van sumando, así que podemos hacer el procedimiento diez veces e ir sumando las potencias.




Las tres líneas iniciales son la declaración de variables. La variables i y j son variables para ciclos, n es la cantidad de divisores que tienen el número, en t el número actual a factorizar, p es el arreglo donde guardamos los números primos y r el arreglo donde guardamos los exponentes. Para determinar el tamaño de p, sabemos que la cantidad de primos que existen en el intervalo es aproximadamente 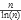=  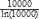≈ 1085 y partiendo de este número lo vamos ajustando hasta llegar a 1229. La función primos de la línea 5 es la misma que utilizamos en la sección 4.4.

La siguiente función es la de factoriza (líneas 7 a 20), en la cual calculamos las potencias de los divisores del parámetro n. Primero inicializamos a cero i, que es la variable con la que vamos a recorrer el arreglo de primos. La parte importante está entre las líneas 13 a 18: nos colocamos en el siguiente primo (línea 13) y si es factor de t, dividimos a t entre este primo (línea 17) e incrementamos el exponente (línea 16). Esto lo repetimos mientras siga dividiendo (línea 14). Es evidente que al irlo dividiendo con todos sus componentes al final va a ser uno, que es lo que revisamos para terminar (línea 11).

En la función numero_factores (líneas 22 a 29) calculamos la cantidad de divisores. Inicializamos n a uno para poder irlo multiplicando (de no hacerlo, la multiplicación siempre sería cero). En la línea 26 recorremos todos los primos y en la 27 multiplicamos el acumulado por uno más que la cantidad del exponente del primo en el que vamos. Para no tener que hacer todo el recorrido hasta el último primo, pudimos haber guardado el último primo al que llegamos en el ciclo en la línea 13 y hacer el ciclo hasta este número.

La parte principal del programa está entre las líneas 31 y 40. Primero mandamos precalcular todos los primos que vamos a utilizar (línea 32) e inicializamos los exponentes a cero. De la 34 a la 38 leemos cado un de los diez números y los mandamos factorizar. Acabamos imprimiendo el último dígito de la cantidad de divisores en la línea 39.

Entrada:	504
Desarrollo:	2  3  5  7 11 13 17 19 504,  0  0  0  0  0  0  0  0 252,  1  0  0  0  0  0  0  0 126,  2  0  0  0  0  0  0  0  63,  3  0  0  0  0  0  0  0  21,  3  1  0  0  0  0  0  0   7,  3  2  0  0  0  0  0  0   1,  3  2  0  1  0  0  0  0 n = (3+1)(2+1)(0+1)(1+1)(0+1)(0+1)(0+1)(0+1) n = (4)(3)(2) = 24 24 ≡ 4 mod 10
Salida:	4

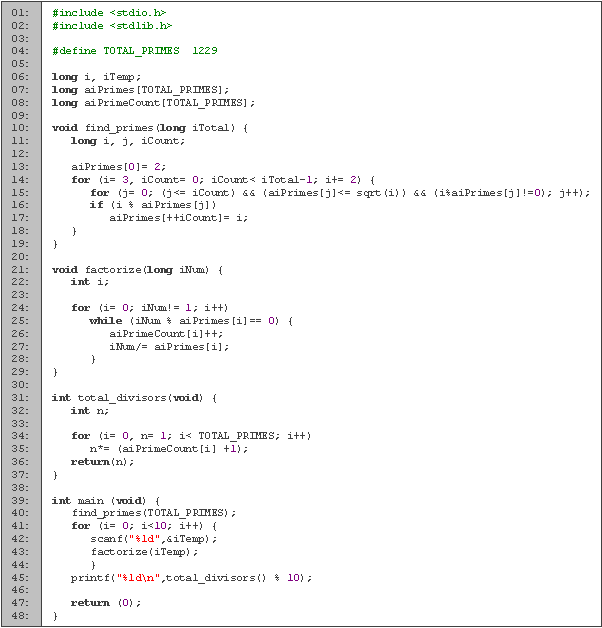
Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	03-Feb-2006	0.001	0.001	0.020	1.984	238
C	03-Feb-2006	0.001				222

Valladollid:

Ural: