Existen diversos métodos para obtener la raíz cuadrada. El que vamos a estudiar es particularmente útil por dos razones: es de fácil implementación y corre razonablemente rápido; aunque su deducción es un tanto compleja por las optimizaciones que se deben usar.

La idea es ir calculando el resultado bit por bit del más al menos significativo. Supongamos que deseamos calcular la raíz de un número x, y el resultado lo vamos a guardar en r. Al final del algoritmo esperaríamos que r = 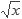, o lo que es lo mismo r² = x. Descomponiendo a r en potencias de dos, definimos a p como la menor potencia de dos tal que p² > x; esto es, p es la potencia que le sigue al bit más significativo de r.

El algoritmo funciona de la siguiente manera. En r vamos guardando una aproximación a la raíz, que al terminar el algoritmo va a ser el resultado exacto. El valor inicial de r es 0, y en cada paso vamos a intentar agregarle una potencia de dos, de tal forma que el nuevo valor de r se acerque más a la solución. La potencia de dos las tenemos que ir agregando de la más a la menos significativa, y para eso vamos a utilizar p, al cual vamos a ir dividiendo entre dos para obtenerlas. Si el valor actual de p ayuda a r a acercarse, sin pasarse, a la raíz de x (o lo que es lo mismo, (r + p)² ≤ x), entonces incrementamos a r en p. Esto lo repetimos hasta que el valor de p sea cero. Por ejemplo, si queremos obtener la raíz de 121, tendríamos:

x	r	p	(r + p)2	(r + p)2 ≤ x
121	0	16	256	no
121	0	8	64	sí
121	8	4	144	no
121	8	2	100	sí
121	10	1	121	sí
121	11	0	121	-

Las divisiones entre dos las podemos cambiar por desplazamientos, pero elevar al cuadrado es una operación costosa (sobre todo con número grandes) por lo que ahora vamos a realizar algunos cambios para optimizarlo. Estamos incrementando r cada que (r + p)² ≤ x, que los podemos descomponer de la siguiente forma r² + 2rp + p² ≤ x. Vamos a definir a t como 2rp + p², entonces la ecuación anterior se convierte en r² + t ≤ x. Despejando t obtenemos t ≤ x -r².

Cada que cambia r, lo podemos expresar en relación a sus valores anteriores como r = r_a + p_a. Sustituyéndolo en la desigualdad anterior, nos quedaría de la siguiente forma t ≤ x – (r_a + p_a)² = x – (r_a² + 2r_ap_a + p_a²), donde podemos sustituir los últimos dos sumandos para obtener t ≤ x –(r_a² + t_a). De manera similar, podemos cambiar r_a² por su valor anterior y repetir esto de manera sucesiva hasta llegar a la r inicial (r₀). Al final alcanzaríamos la expresión t ≤ x – (r₀² + t_a + t_a-1 + … + t₀), y como el valor inicial de r es cero, la expresión queda como t ≤ x – (t_a + t_a-1 + … + t₀). Para no tener que estar guardando los valores anteriores de t, redefinimos a la variable x como x = x_a –t_a. Esto es, ahora x no es el número original al cual sacarle raíz, sino la diferencia entre la aproximación y el número original. Con esto, la desigualdad sería simplemente t ≤ x.

Revisemos el ejemplo anterior con estos cambios (recordemos que t = 2rp + p²):

x	r	p	t	t ≤ x
121	0	16	256	no
121	0	8	64	sí
57	8	4	80	no
57	8	2	36	sí
21	10	1	21	sí
0	11	0	0	-

En realidad, ahora estamos efectuando más cálculos que antes y seguimos utilizando cuadrados, pero podemos mejorar el método con el que obtenemos t. Sabemos que t = 2rp + p², y si definimos a s = 2rp y m = p², podemos expresarlo como t = s + m. Como m es p², al momento de encontrar el valor inicial de p podemos encontrar el de m; y como el valor de p lo actualizamos dividiendo entre 2, el de m lo hacemos dividiendo entre 4.

El valor de s es un poco más complicado de actualizar ya que el valor de r va cambiando y queremos evitar hacer la multiplicación entre r y p. Tenemos que s = 2rp y que a p lo dividimos por dos en cada ciclo, por lo que si el valor de r no ha cambiado, podemos actualizar s dividiéndolo entre dos. En caso de que r sí haya sido modificado, podemos calcular s considerando como cambiaron los valores de r y p (p = 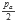 y r = r_a + p_a). Por lo tanto, s = 2rp = 2(r_a + p_a)(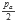) = r_ap_a + p_a². Ahora vamos a ponerlo en términos de t_a y m_a (t_a = 2r_ap_a + p_a², y m_a = p_a²). Con esto tenemos que s = r_ap_a + p_a² = 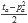+ p_a² = 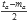+ m_a = .

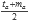Los pasos siguen siendo los mismos, pero ahora t lo podemos actualizar utilizando solo sumas y divisiones entre potencias de dos:

x	r	p	t	m	s	t ≤ x
121	0	16	256	256	0	no
121	0	8	64	64	0	sí
57	8	4	80	16	64	no
57	8	2	36	4	32	sí
21	10	1	21	1	20	sí
0	11	0	0	0	11	-

Por último, podemos observar que al final s y r son iguales. Esto no es coincidencia, y se debe a que como s = 2rp, y como en el últimos ciclo al dividir p pasaría de 1 a ½, tenemos que s = r (aunque para nosotros p pasa a 0, porque estamos utilizando naturales, pero esto no afecta el calcula de s). Dado que r sólo la utilizamos para guardar el resultado, pero este lo podemos obtener de s, vamos eliminar el uso de r.

Si lo que deseáramos obtener fuera la raíz n-ésima, una estrategia simple consiste en implementar la potenciación e ir cambiando el valor de la base mediante una búsqueda binaria hasta que obtengamos el resultado.




Solución: Lo que nos están pidiendo es encontrar una y tal que y² ≤ x. Esto implica que y ≤ 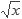, que es el algoritmo que acabamos de estudiar.





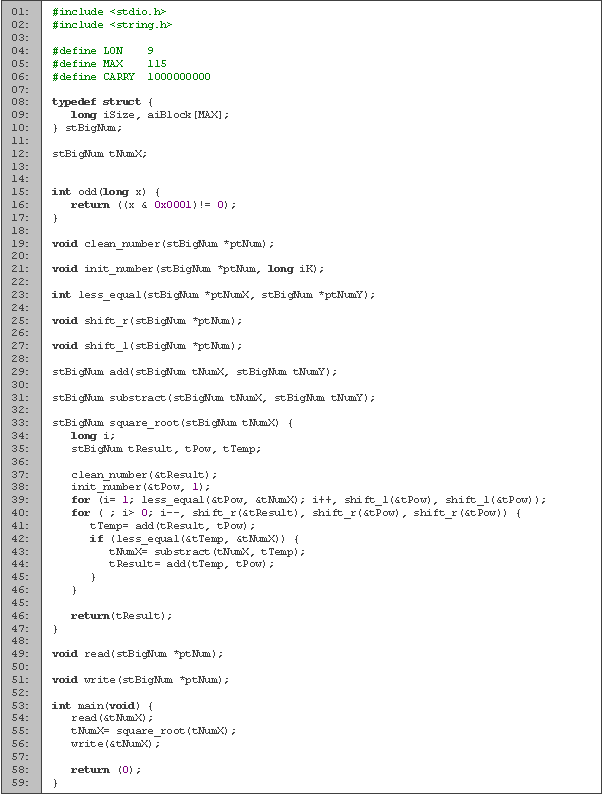
Las constantes y la definición de los números grandes (líneas 1 a 10) son las mismas que en los problemas anteriores. El único cambio es el tamaño de max, que lo calculamos de la siguiente forma: 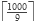 y dejamos algunos bloques extra por precaución.

Entre la líneas 12 y 13 declaramos la única variable que vamos a emplear, la cual nos va a servir para leer el número y para guardar su raíz.

Muchas funciones y procedimientos son los mismos que empleamos en problemas anteriores, por lo que vamos a obviarlos.

La función más importante es, desde luego, con la que obtenemos la raíz, que se encuentra de la línea 29 a la 53. Las variables x, m y t están definidas de acuerdo a la explicación que dimos anteriormente, mientras que r reemplaza a s, p ya no es la potencia sino sólo el exponente, y el entero i nos sirve para los ciclos. Las líneas 33 y 34 las usamos para inicializar las variables.

En el primer ciclo (líneas 36 a 40), calculamos la cantidad de bits que va a tener el resultado, para en el siguiente ciclo calcular el resultado bit por bit de acuerdo al algoritmo. Calculamos el valor de t en la línea 3, y en caso de que sea menor o igual a x, cambiamos el valor de x y actualizamos r. Terminamos realizando los desplazamientos correspondientes.

La parte principal (líneas 76 a 80) es directa: leemos el número, sacamos la raíz y la imprimimos.

Entrada:	125
Desarrollo:	m     x   1 ≤ 125, p= 1   4 ≤ 125, p= 2  16 ≤ 125, p= 3  64 ≤ 125, p= 4 256 > 125, p= 5  t     x 256 > 125, m= 256, r=   0  64 ≤ 125, m=  64, r= 128  80 >  61, m=  16, r=  64  36 ≤  61, m=   4, r=  40  21 ≤  25, m=   1, r=  11         4
Salida:	11

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	16-Feb-2006	0.067	0.040	-	-	153
C	16-Feb-2006	0.067				366

Valladollid:

Ural:

Project Euler: