El módulo es el residuo de la división, por lo que el algoritmo es el mismo en ambos casos y solamente cambia el valor que devuelve la función. Igual que con la multiplicación, utilizamos un método en base dos descubierto por los antiguos egipcios.

Antes de empezar a analizar el método, recordemos el nombre de los operandos y los resultantes en la división:

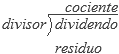
Supongamos que queremos dividir un número x entre un número y teniendo como cociente r y como residuo m. Para dividir lo que hacemos es ir multiplicando por dos al divisor y mientras que no sea mayor que el dividendo x. Nos acordamos del tema anterior que multiplicar por dos es equivalente a un desplazamiento a la izquierda, y que este último es mucho más rápido. Guardamos la cantidad de multiplicaciones que efectuamos en p. De esta forma obtenemos que:
x = 2^p×y + s
Donde s es el sobrante de x con respecto a 2^p×y. Tomamos a s y repetimos todo el proceso. Esto lo seguimos efectuando hasta que el sobrante que tengamos sea menor que el divisor. Al final tendremos algo de la forma:
x = 2^p₀×y + 2^p₁×y + … + 2^p_k×y + s_k
Como el sobrante es menor el divisor, es equivalente el residuo (esto es, s_k se convierte en m). Factorizando y obtenemos:
x = (2^p₀ + 2^p₁ + … + 2^p_k)×y + s_k
y sabemos que:
x = r×y + m
Por lo tanto, el resultado de la división r lo podemos obtener sumando todas las potencias de dos que utilizamos.

De manera similar a la multiplicación, el tiempo de ejecución es O(n²) y existen mejores algoritmos. Uno de los más utilizados se basa en técnicas “divide y vencerás” pero requiere una muy buena implementación de la multiplicación (óptimamente, la efectuada con la Transformada Rápida de Fourier).




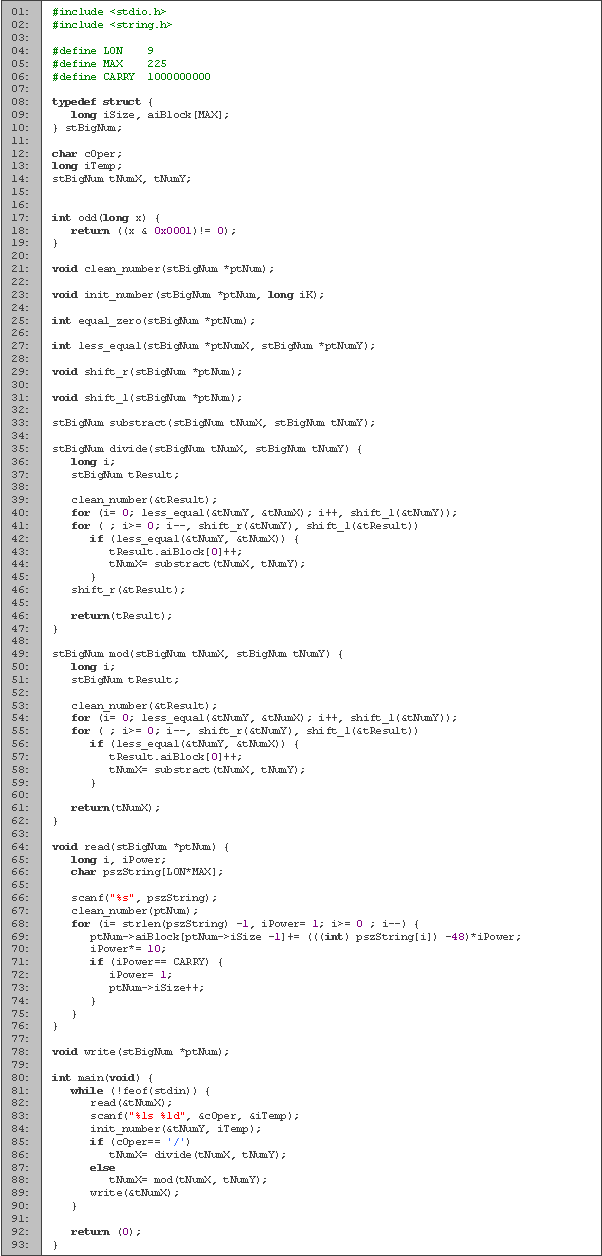
Solución: Al igual que con el problema anterior, sólo debemos implementar los algoritmos para hacer las operaciones que nos piden. Por el tamaño n, podríamos implementar una división de un número grande entre un longint. No lo vamos a hacer así por fines didácticos.





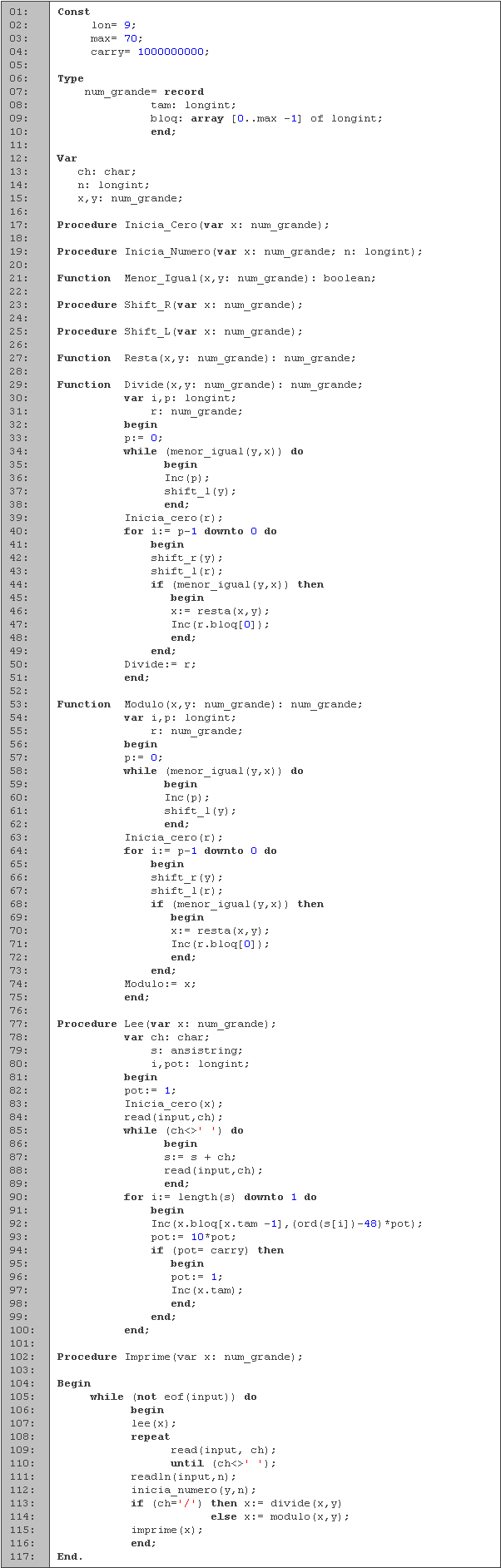
Las primeras 10 líneas son casi las mismas que en el problema anterior. Definimos el tamaño de los bloques, el número máximo de bloques, el modulo a utilizar y la estructura de los números grandes. La única diferencia es el número máximo de bloques a utilizar.

En este caso, en ninguna parte del problema mencionan el tamaño máximo del número y se limitan a decir que pueden ser arbitrariamente grandes. Tenemos varias alternativas a seguir dependiendo de la situación en la que nos encontremos. Una opción es crear una implementación dinámica de número grandes. Otras alternativas son: si nos encontramos en un concurso, podemos preguntar el tamaño a los jueces; dentro de un concurso en línea, podemos sobredimensionar tanto como nos lo permita la memoria disponible; y si estamos entrenando, podemos hacerlo a prueba y error, o entrar a los foros y esperar que alguien ya halla obtenido un acotamiento.

Las siguientes cuatro líneas de código (líneas 12 a 15) son donde declaramos las variables a utilizar. En el caracter ch vamos a guardar la operación a realizar, dentro de n guardamos el segundo número (el divisor), y las variables x e y nos sirven para realizar las operaciones con los números grandes.

Las funciones y procedimientos inicia_cero (línea 17), inicia_numero (línea 19), menor_igual (línea 21), shift_r (línea 23), shift_l (línea 25), resta (línea 27) e imprime (línea 102) son los mismos que se emplearon en el problema anterior y que implementamos en secciones anteriores.

La funciones divide (líneas 29 a 51) y modulo (líneas 53 a 75) son el mismo código excepto que devuelven resultados distintos. Tomando como referencia divide, en las líneas 33 a 38 vamos desplazando el divisor hasta que se vuelve más grande que el dividendo. La cantidad de desplazamientos que realizamos lo guardamos en p. En la línea 39 iniciamos el resultado de la división a cero. Después, por cada corrimiento a la izquierda que hicimos, vamos a efectuar uno a la derecha. Si el divisor es menor o igual al dividendo, se lo restamos e incrementamos en 1 el resultado. El resultado lo desplazamos un lugar a la izquierda en cada ciclo.

Esperaríamos que si el divisor es menor o igual, el resultado lo deberíamos incrementar en 2ⁱ. Para evitar hacer esto lo incrementamos en 1 y lo desplazamos en cada ciclo. Veamos porque funciona: al incrementar en 2ⁱ equivale a agregar un 1 en la posición i del número en binario. Esto lo cambiamos por incrementar la posición 0, y al recorrer el número i veces queda en su posición esperada.

En el procedimiento lee (líneas 77 a 100) tenemos una ligera variación: en lugar de leer el número en una sola línea, tenemos que leerlo hasta encontrar un espacio. Para hacer esto, cambiamos el readln por las instrucciones que se encuentran de la línea 84 a 89. Esto es, auxiliarnos de una variable temporal ch para leer los caracteres y anexarlos de uno en uno a la cadena.

Terminamos con la parte principal del código (líneas 104 a 117), donde leemos los números y la operación a evaluar, y la realizamos. Hacemos esto mientras no lleguemos al fin de archivo.

Entrada:	417 / 29
Desarrollo:	y     x 29  ≤ 417, p= 0 58  ≤ 417, p= 1 116 ≤ 417, p= 2 232 ≤ 417, p= 3 464 > 417 232 ≤ 417, r= 1 116 ≤ 185, r= 3 58  ≤  69, r= 7 29  >  11, r= 14        11
Salida:	14

Entrada:	253 % 13
Desarrollo:	y     x 13  ≤ 253, p= 0 26  ≤ 253, p= 1 52  ≤ 253, p= 2 104 ≤ 253, p= 3 208 ≤ 253, p= 4 416 > 253 208 ≤ 253, r= 1 104 >  45, r= 2 52  >  45, r= 4 26  ≤  45, r= 9 13  ≤  19, r= 19         6
Salida:	6

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	16-Feb-2006	0.031	0.000	0.004	3.469	Minimum
C	16-Feb-2006	0.029				Minimum