Queremos saber si dos rectas se intersectan, y en caso de que lo hagan, poder determinar en que punto fue. A la recta la vamos a representar utilizando dos de sus puntos, por lo que podemos utilizar la misma ecuación de la sección anterior:
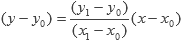
Mientras que una segunda recta estará representada por:
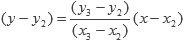
Necesitamos determinar si las rectas son paralelas para saber si se intersectan o no. Esto lo podemos obtener comparando sus pendientes. En caso de que sean iguales, es porque las líneas son paralelas. Cuando esto sucede, las rectas no pueden intersectarse a menos de que sus ecuaciones sean equivalentes (con lo que se intersectarían en una infinidad de puntos).
Para saber si son la misma recta, tomamos x = 0, y los valores de y tienen que ser iguales, por lo que:
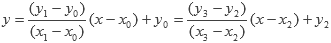mA(-x0) + y0 = mB(-x2) + y2
Si ya sabemos que las pendientes son distintas, para obtener en que punto se intersectan podemos hacer lo siguiente. Despejamos y de las dos ecuaciones e igualamos:
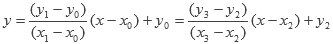mA(x-x0) + y0 = mB(x-x2) + y2mAx -mAx0 + y0 = mBx -mBx2 + y2
x(mA-mB) = mAx0 -mBx2 + y2 -y0
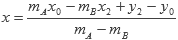
Teniendo el valor de x, podemos calcular y utilizando cualquiera de las dos ecuaciones iniciales.
Problema ejemplo
Líneas en Intersección
Problema
Todos sabemos que un par de puntos distintos en un plano definen una línea y que un par de líneas en un plano pueden ser contempladas de acuerdo a alguno de los tres casos de intersección: 1) no hay intersección porque son paralelas, 2) la intersección es una línea ya que una está encima de la otra (es decir, son la misma línea), 3) intersectan en un punto. En este problema debes usar tus conocimientos algebraicos para crear un programa que determine como y donde dos líneas se intersectan.Tu programa debe leer repetidamente cuatro puntos que definen dos líneas en el plano x-y y determinar como y donde se intersectan. Todos los números requeridos para el problema estarán en un rango razonable, digamos entre -1000 y 1000.
Entrada
La primera línea contiene un entero n entre 1 y 10 que describe cuantas parejas de líneas serán representadas. Las siguientes n líneas contendrán cada uno a ocho enteros. Estos enteros representaran las coordenadas de cuatro puntos en el plano en el siguiente orden x1 y1 x2 y2 x3 y3 x4 y4. Por lo tanto, cada una de estas líneas de entrada representaran dos líneas en el plano: la línea que pasa por (x1, y1) y (x2, y2), y la línea que pasa por (x3, y3) y (x4, y4). El punto (x1, y1) siempre es distinto a (x2, y2). Lo mismo pasa con (x3, y3) y (x4, y4).Salida
La salida deberá tener n+2 líneas. En la primera se deberá escribir “INTERSECTING LINES OUTPUT”. Habrá una línea de salida por cada pareja de líneas en el plano representadas por en la entrada, describiendo como se intersectan las líneas: 'NONE' en caso de que no lo hagan, 'LINE' si son la misma línea o 'POINT' si se intersectan en un punto. Para el último caso tu programa también deberá escribir las coordenadas x e y del punto, con dos decimales de precisión. En la última línea de la salida se deberá escribir “END OF OUTPUT”.Solución: Aplicamos las fórmulas que acabamos de obtener, teniendo cuidado de revisar los casos el los que las pendientes son iguales.
Código
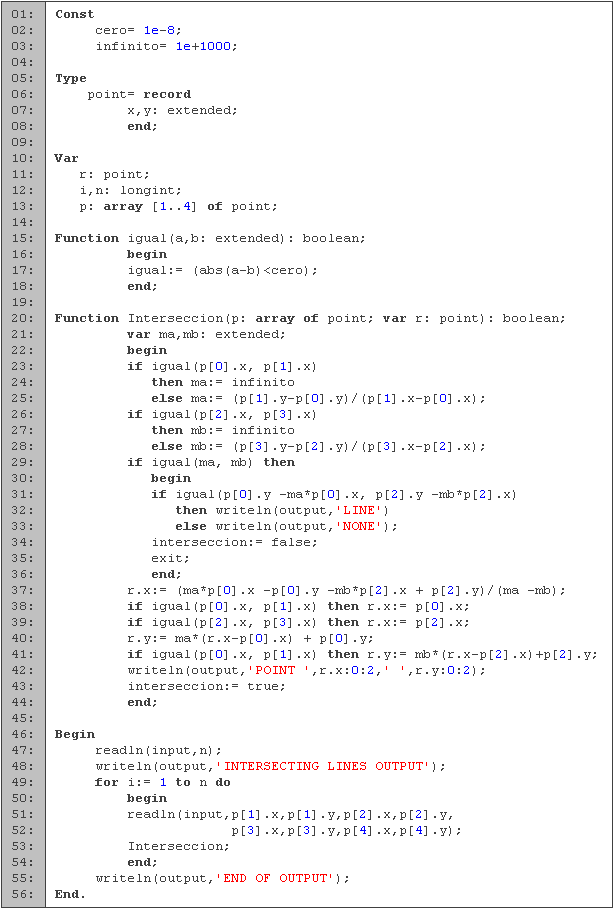
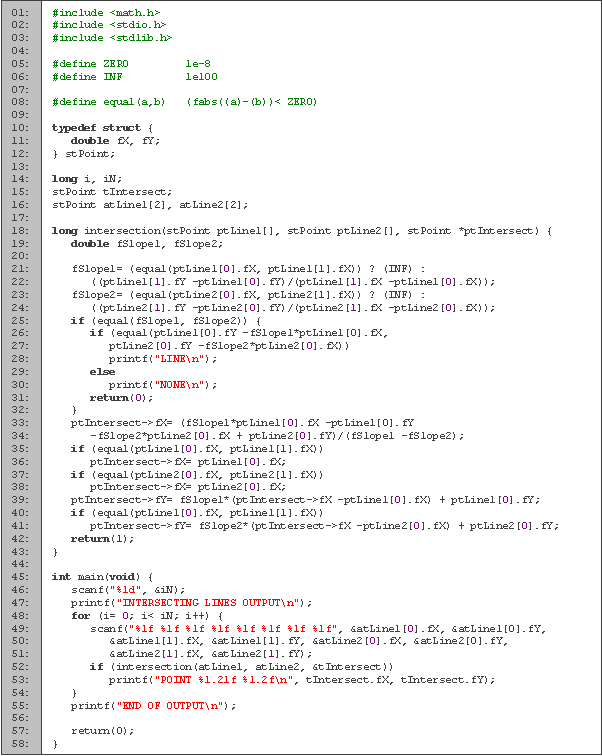
En las primeras tres líneas definimos las constantes a utilizar, y después definimos la estructura de un punto, como lo hicimos en el problema anterior. Entre las líneas 10 y 12 declaramos las variables que vamos a utilizar. En n leemos la cantidad de casos y utilizamos i para los ciclos. Para leer los puntos por los que pasa la recta utilizamos el arreglo p, y guardamos el resultado en r.
Como vamos a estar realizando comparación continuamente, escribimos la función igual (líneas 15 a 18) que nos ayuda saber si un número flotante es igual a otro, tomando en cuenta el error de tolerancia. Consideramos que son iguales si su diferencia es menor a nuestra tolerancia.
En seguida tenemos la función interseccion (líneas 20 a 44) que es donde determinamos si las rectas se intersectan. La función devuelve true cuando la rectas se intersectan en un punto y false en caso contrario. Como parámetros tenemos un arreglo de puntos p, donde los primeros dos puntos representan la primera recta, y los siguientes dos la segunda, y la variable r que es donde guardamos el resultado. En la línea 21 declaramos las variables ma y mb que utilizaremos para calcular las pendientes.
Empezamos calculando las pendientes (líneas 23 a 28). Si éstas son iguales, revisamos si se trata de la misma línea (línea 32) o si son paralelas (línea 33), para después asignarle false a la función y salirnos. Como buscamos el punto donde se intersectan, si son la misma línea estamos considerando que no existe (como único), pero es posible cambiar esta condición si se desea, sólo habría que asignarle a r cualquier valor de la recta (que puede ser algún valor de p). Después encontramos el valor de r en las líneas 37 y 40. Tenemos condiciones especiales cuando el valor de alguna pendiente es infinita (líneas 38, 39 y 41), ya que nuestro valor puede dar resultados inexactos. Terminamos escribiendo el resultado y devolviendo true en la función.
Aunque es posible no utilizar la función igual (comparando directamente los valores) o quitar los casos de las líneas 38 y 39, y aún así tener aceptado el problema, es mejor siempre considerar este tipo de casos. En este problema (y en algunos otros), la coordenadas son enteros relativamente pequeños, por lo que es difícil que hayan errores de precisión en las operaciones intermedias, pero esto no nos garantiza que no vayan a existir.
Caso ejemplo
| Entrada: | 3 0 0 4 4 0 4 4 0 5 0 7 6 1 0 2 3 5 0 7 6 3 -6 4 -3 |
| Desarrollo: | ma= (0-4)/(0-4)= 1; mb= (0-4)/(4-0)= -1; ma<> mb x= (1*0 –0 -(-1)*0 +4)/(1 –(-1)) = 4/2= 2 y= 1(2-0) + 0 = 2 ma= (0-6)/(5-7)= 3; mb= (0-3)/(1-2)= 3; ma = mb 0 –3*5<> 0 –3*1 ma= (0-6)/(5-7)= 3; mb= (-6 –(-3))/(3-4)= 3; ma = mb 0 –3*5 = -6 –3*3 |
| Salida: | INTERSECTING LINES OUTPUT POINT 2.00 2.00 NONE LINE END OF OUTPUT |
Código en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 04-Jun-2006 | 0.000 | 0.000 | 0.000 | 0.050 | Minimum |
| C | 15-Jun-2006 | 0.000 | Minimum | |||
Máximo número de puntos en una recta
