Teniendo esparcidos por el plano una cantidad finita de puntos, queremos encontrar la cantidad máxima de los mismos que se encuentren alineados, es decir, que podemos trazar una línea recta que los cubra.

Sabemos que teniendo dos puntos, la ecuación de la recta que pasa por ellos es (con x₁ ≠ x₀):

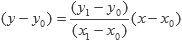
Para saber si un tercer punto es colineal a los dos anteriores, se tiene que cumplir que:

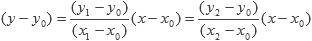
Por lo que:

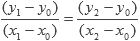
Esta ecuación nos indica que para que tres puntos sean colineales, necesitamos que al escoger cualquier combinación de dos de ellos, la pendiente debe ser la misma (y por lo tanto, también el ángulo de inclinación de la recta). Debemos tener cuidado con los valores x₁ = x₀ y x₂ ≠ x₀, en los cuales la pendiente se vuelve infinita.




Solución: Nos piden el número máximo de conejos (puntos) en una recta, y para obtenerlo vamos a utilizar la fórmula anterior sobre todas las combinaciones de puntos posibles.





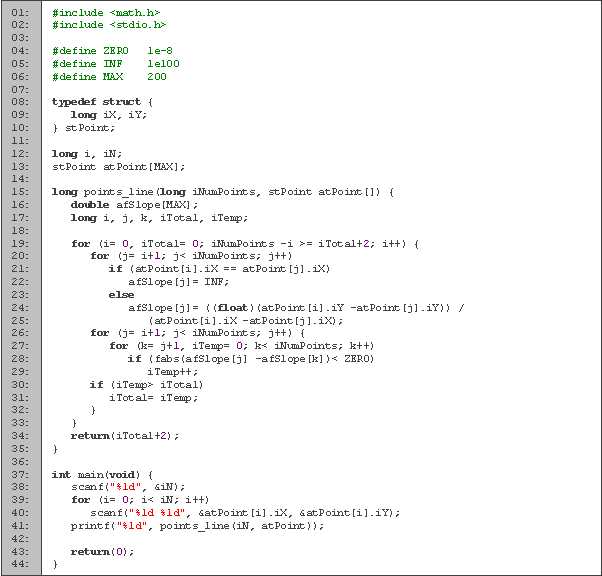
En las primeras tres líneas tenemos las constantes que vamos a utilizar. Como vamos a realizar operaciones con puntos flotantes, necesitamos una tolerancia para los errores de redondeo, por lo que definimos la constante cero como el menor valor significativo que vamos a utilizar. A este valor muchas veces se le denomina error o rango de error. También necesitamos definir el valor de infinito, ya que es un valor que puede tomar la pendiente. Los dos valores se tomaron de manera empírica y funcionan bien para la mayoría de las veces, aunque habrá problemas que requieran mayor precisión.

Entre las líneas 5 y 8 definimos la estructura point para guardar las coordenadas de un punto. Después tenemos la declaración de variables (líneas 10 a 12). En la variable n leemos la cantidad de puntos, i la utilizamos para los ciclos y el arreglo p para guardar los puntos.

Calculamos la cantidad de puntos en una recta en la función de las líneas 14 a 35. Declaramos las variables locales en las líneas 15 y 16. Para los ciclos utilizamos i, j y k, t para contar cuantos puntos en línea llevamos y r para guardar el resultado. Empezamos inicializando el resultado en línea 18. Para generar todas las parejas de puntos, hacemos un ciclo de i igual 1 hasta n-1 (línea 19), y de j igual a i+1 hasta n (línea 22). No hacemos los de ciclos de 1 a n porque para calcular el valor de la pendiente, el orden en que tomemos los puntos no importa, y porque i tiene que ser distinto a j. En la línea 24 calculamos la pendiente entre los puntos i y j, y los guardamos en el arreglo en la casilla j. Para evitar divisiones entre cero, agregamos un caso especial donde la pendiente es infinita (línea 25). Entre las líneas 26 y 32 comparamos los valores de las pendientes y cada que encontramos una igual, incrementamos t (línea 30). Si al final el valor de t es mayor que nuestro resultado, le asignamos al resultado el valor de t. Cuando terminemos, vamos a tener en r el mayor número de pendientes iguales, al cual le añadimos 2 para el número de puntos en una misma línea. La condición de la línea 21 sirve para salirnos si con la cantidad de puntos que sobran no se puede obtener un mejor resultado.

La parte principal del código la encontramos entre las líneas 27 y 42. Empezamos leyendo la cantidad de puntos (líneas 38) para después leer las coordenadas de estos (líneas 38 y 39) y terminar escribiendo cuantos hay que estén en línea recta.

Entrada:	6 7 122 8 139 9 156 10 173 11 190 -100 1
Desarrollo:	i  m 1  -- 17 17 17 17 1.131; t= 3; r= 3 2  -- -- 17 17 17 1.278; t= 2; r= 3 3  -- -- -- 17 17 1.422; t= 1; r= 3 4  -- -- -- -- 17 1.564; t= 0; r= 3 5  -- -- -- -- -- 1.703; t= 0; r= 3 r + 2 = 5
Salida:	5

Nota: En el ejemplo no estamos considerando la condición de la línea 21 para ver el funcionamiento del algoritmo.



Esta claro que el tiempo en el que corre este algoritmo es de O(n³). Podemos reducir este tiempo a O(n²lgn) haciendo un cambio. Una vez que tenemos las pendientes en cada ciclo de i, el siguiente paso es ver cuantas son iguales. Para hacerlo de una manera más rápida, vamos primero a ordenar el arreglo y después sólo tenemos que revisar casillas adyacentes para saber cuantas pendientes son iguales.

El procedimiento quicksort es el mismo que estudiamos en la sección 3.3, y podemos utilizar cualquier otra ordenación que tenga un tiempo menor a O(n²). En la función PuntLinea, cambiamos las líneas 26 a 32 en el algoritmo anterior por las líneas 15 a 24 en este. Empezamos ordenando el arreglo en los valores que toma j. Mientras las casillas adyacentes sean iguales, incrementamos la cuenta (línea 19) y cuando no, la reiniciamos (línea 22). Cuando terminamos o reiniciamos, revisamos si el valor que tenemos es mayor que el resultado actual (líneas 21 y 24).

Algo importante es que al pasar un arreglo como parámetro en Pascal de tamaño n, al utilizarlo dentro de la función o procedimiento las casillas irán de 0 a n-1. Por ejemplo, si definimos un arreglo de tamaño [3..10], dentro de la función el rango del arreglo es de [0..7]. Por eso los parámetros del procedimiento quicksort son i y n-1, en lugar de i+1 y n (que son los valores que toma j).

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	22-Mar-2006	0.031	0.001	0.078	1.781	126
C	27-Abr-2006	0.015				138
Pascal	22-Mar-2006	0.015				126
C	02-May-2006	0.015				138

Valladollid:

World Archive: