Teniendo un conjunto de puntos en el plano, su envoltura convexa (o casco convexo) está definida por el polígono convexo de área mínima que cubre todos los puntos (esto es, todos los puntos están dentro del polígono). Esta definición también se puede generalizar para puntos en el espacio o para puntos en alguna dimensión mayor, cambiando el polígono por un poliedro. Como la mayoría de los problemas geométricos en concursos son en segunda dimensión, sólo vamos a estudiar este caso.
Al igual que con los problemas de ordenación, existen muchos algoritmos que sirven para calcular la envoltura convexa y para determinar cuál es mejor, depende mucho de la aplicación en la que se va a utilizar. El algoritmo que vamos a utilizar se conoce como Graham Scan, es uno de los más eficientes y es relativamente sencillo de entender e implementar.
Podemos diferenciar dos tipos de puntos de nuestro conjunto: los que van a formar parte del polígono convexo y los que van a estar dentro de él. Para encontrar los puntos que forman parte del polígono, sabemos que los que tienen mayor y menor valor en x e y deben pertenecer al polígono. Al empezar buscamos al punto con menor valor en y, y en caso de que existan varios, desempatamos tomando el menor valor en x.
Después tomamos este punto y ordenamos a los demás de acuerdo al ángulo que forman con este. Calcular el valor del ángulo es una operación costosa, por lo que podemos reemplazarlo calculando solamente la pendiente u ordenando mediante el giro de los segmentos compuestos por el primer punto y los demás.
Para saber si un polígono es convexo podemos hacer lo siguiente. Recorriendo todos los vértices en orden (horario o anti-horario), debemos dar la vuelta siempre hacia el mismo lado (derecha para horario e izquierda para anti-horario). Cuando queremos saber si al llegar a un vértice la vuelta la damos a la izquierda o a la derecha, no necesitamos calcular los ángulos, sino que podemos utilizar el producto cruz entre las aristas que son adyacentes al vértice.
Aprovechamos esto para formar la envoltura convexa. Partiendo del punto que encontramos, y después de ordenarlos, consideramos al siguiente punto también como parte de la envoltura y para los sobrantes hacemos lo siguiente: tomamos los dos puntos anteriores y vemos si a este punto llegamos girando a la izquierda o a la derecha del anterior. Si está a la izquierda, lo guardamos como parte de la envoltura convexa, pero si está a la derecha, quitamos al punto anterior como parte de la envoltura convexa y repetimos hasta que el giro sea a la izquierda.
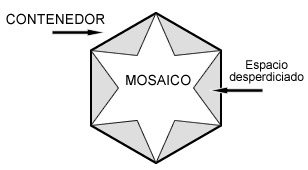
Los dirigentes de EIM están interesados en saber cual es porcentaje de espacio desperdiciado para un mosaico dado.
La entrada terminara con un valor de 0 para n.
Solución: Primero calculamos el área de polígono (Ap), después el área de la envoltura convexa (AE), y el espacio desperdiciado está dado por:
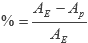 .
.
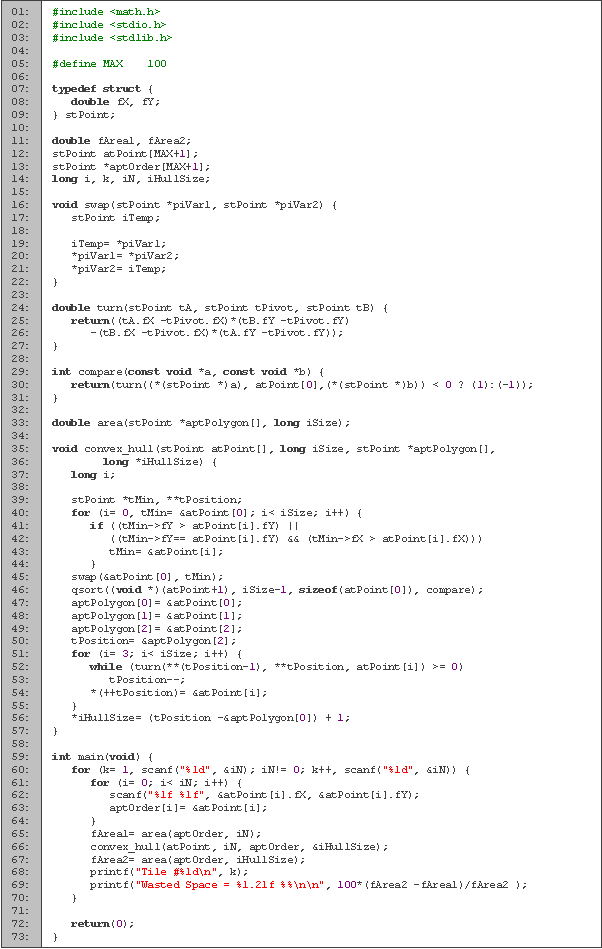
En las primeras cuatro líneas definimos el tipo de variable de un punto. A continuación tenemos la declaración de variables. Las áreas las guardamos en las variables a1 y a2, en k contamos la cantidad de casos que hemos procesado, en n leemos la cantidad de puntos con los que cuenta el polígono y usamos i para los ciclos. Los puntos del polígono original los guardamos en d, y en c guardamos cuales puntos del polígono original pertenecen a la envoltura convexa.
En la función turn (líneas 12 a 15), estamos calculando el producto cruz entre los vectores
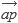 y
y 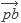 . El resultado del producto cruz es positivo cuando se da una vuelta a la izquierda, negativo cuando es a la derecha y cero en caso de que sean colineales.
. El resultado del producto cruz es positivo cuando se da una vuelta a la izquierda, negativo cuando es a la derecha y cero en caso de que sean colineales.En la línea 17 tenemos la función para calcular el área, que es la misma función que vimos en la sección anterior. Después tenemos la función para ordenar (líneas 19 a 36), que es similar a la que hemos estado utilizando pero que ordena de acuerdo a los giros. Podemos ver los cambios en las líneas 26 y 27.
Continuamos con la función que calcula la envoltura convexa (líneas 38 a 59). Tomamos como parámetros el arreglo que contiene los vértices del polígono (a), el arreglo donde guardaremos los índices de los puntos que son partes de la envoltura convexa (stack) y la cantidad de vértices (n). Como variables tenemos t que utilizaremos como variable temporal, i para los ciclos, min para guardar el índice del punto con el que empezaremos y ps para saber cuantos puntos tenemos en la envoltura convexa.
Empezamos buscando el punto de menor valor en y, desempatando en x (líneas 43 a 47), que será nuestro primer punto en la envoltura. Después mandamos este punto a la primera casilla (línea 48) y ordenamos los puntos (línea 49). Una vez ordenados, guardamos en el arreglo stack los puntos 0, 1 y 2, e igualamos la cantidad de datos a tres. Los puntos 0 y 1 forzosamente van en la envoltura, el 2 no necesariamente pero sabemos que tiene un giro hacia la izquierda con respecto a los dos anteriores. Para cada uno de los puntos sobrantes (líneas 51 a 57) vemos el giro que hacen con los dos puntos anteriores, y mientras el giro sea positivo quitamos el punto anterior (líneas 53 y 54). Proseguimos agregando el nuevo punto (líneas 55 y 56). Al terminar, asignamos a la casilla cero la cantidad de puntos que componen la envoltura convexa.
| Entrada: |
5 0 0 2 0 2 2 1 1 0 2 5 0 0 0 2 1 3 2 2 2 0 0 |
| Desarrollo: |
min= 0 orden: (0,0), (2,0), (1,1), (2,2), (0,2) giro(1,2,3): + giro(0,1,3): - giro(1,3,4): - envoltura: 0 1 3 4 a1= 3; a2= 4; min= 0 orden: (0,0), (2,0), (2,2), (1,3), (0,2) giro(1,2,3): - giro(2,3,4): - envoltura: 0 1 2 3 4 a1= 5; a2= 5; |
| Salida: |
Tile #1 Wasted Space = 25.00 % Tile #2 Wasted Space = 0.00 % |
Podemos ver que estamos eliminando los puntos no sólo cuando el giro es a la derecha, sino también cuando no hay giro (línea 53). Esto se debe a que cuando el giro es igual a cero, los puntos son colineales. Estos puntos los podemos considerar como parte de la envoltura convexa pero no agregan información valiosa y como muy posiblemente necesitemos realizar cálculos después, entre menos puntos tenga la envoltura, más rápido se ejecutarán los algoritmos.
La complejidad de este algoritmo depende del tiempo en que ordenamos. Dado que tenemos una Ordenación Rápida de Hoare, la complejidad es de O(nlgn). Como tenemos un while dentro de un for, parece como si esta parte fuera O(n2) pero cada punto es agregado o removido del arreglo sólo una vez por lo que es O(n).
Graham Scan es una muy buena opción para puntos en el plano pero tiene el inconveniente de que no puede ser generalizado a dimensiones más altas. Para tercera dimensión y otras dimensiones mayores, podemos utilizar un concepto a la Ordenación Rápida de Hoare para encontrar un algoritmo conocido como QuickHull. Existen otras opciones, pero ésta es generalmente la más utilizada.
La función turn también la podemos utilizar para saber si un punto está dentro o fuera de un polígono convexo, utilizando un enfoque similar al que utilizamos para encontrar la envoltura convexa.
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 01-Jun-2006 | 0.000 | 0.000 | 0.002 | 9.791 | Minimum |
| C | 04-Jul-2006 | 0.002 | Minimum | |||
Valladollid:
 Área de un polígono
Área de un polígono
