Teniendo las coordenadas cartesianas de un polígono con n vértices, podemos encontrar su área mediante la fórmula:

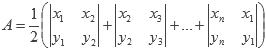
Resolviendo la determinante tenemos que:

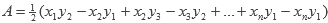
Si agregamos un punto extra al polígono que sea igual al primero, obtenemos:

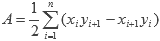
La fórmula no requiere que el polígono sea convexo, pero si se necesita que no sea estrellado. Los vértices deben estar ordenados ya sea de forma horaria o anti-horaria, donde el signo del resultado depende de cual de estos dos ordenamientos fue utilizado.

Decimos que un polígono es convexo cuando podemos escoger dos puntos cualesquiera dentro de él y la línea recta que los une no sale del polígono. Decimos que un polígono es estrellado cuando algunos de sus lados se intersectan.





Las primeras tres líneas son la definición de un punto, como la habíamos utilizado anteriormente. La función area es la que nos devuelve el área de un polígono. Como entradas tenemos el arreglo de puntos p y el arreglo de entero c. En p guardamos las coordenadas de los vértices del polígono, mientras que en c guardamos el orden en que vamos a recorrerlos y en la casilla 0 de c guardamos cuantos puntos son. La variable i la utilizamos para los ciclos y a para ir guardando la suma.

Empezamos inicializando la suma a cero (línea 10), después utilizamos la fórmula para calcular el área (líneas 11 y 12) y devolvemos el valor absoluto del resultado (línea 13). Puede parecer redundante el arreglo c, pero dentro en la siguiente sección se verá su utilidad.






Valladollid: