El incírculo (o círculo inscrito) es el círculo de mayor diámetro que se puede inscribir dentro de un polígono (en este caso, un triángulo). El circuncírculo de un triángulo es el único círculo que pasa por los tres vértices.
El incírculo del triángulo es tangente a sus tres lados. Al centro se le conoce como incentro y es donde se intersectan las tres bisectrices de los ángulos internos. Al radio del incírculo se le conoce como inradio y lo representaremos mediante r.
El circuncírculo es el círculo más pequeño que contiene a cualquier triángulo agudo, pero no pasa lo mismo con los obtusos. Al centro del circuncírculo se le conoce como el circuncentro, y se encuentra en la intersección de las tres mediatrices. Al radio del circuncírculo se le denomina circunradio y lo nombraremos R.
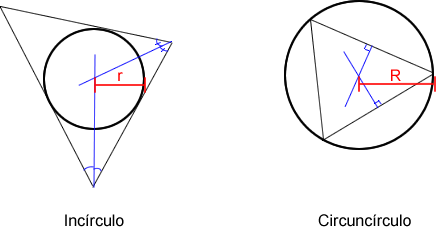 |
| Figura 7.2: Incírculo y circuncírculo de triángulos |
Teniendo un triángulo con lados de tamaño a, b y c, ángulos a, b y c, área A y semiperímetro s tenemos que:
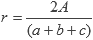
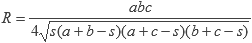
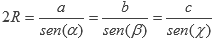
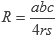
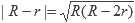
Problema ejemplo
Círculo A Través de Tres Puntos
Problema
Tu equipo deberá escribir un programa que, dadas las coordenadas cartesianas de tres puntos en el plano, encuentre la ecuación del círculo que atraviese a los tres. Los tres puntos no formarán una línea recta.La solución deberá ser escrita como una ecuación de la forma:
(x -h)2 + (y -k)2 = r2 (1)
y una ecuación de la forma:
x2 + y2 + cx + dy + e = 0 (2)
Entrada
Cada línea de la entrada contendrá las coordenadas x e y de tres puntos, en el orden Ax, Ay, Bx, By, Cx, Cy. Cada una de estas coordenadas estarán compuestas por números reales, separados unos de otros mediante uno o más espacios en blanco.Salida
Tu programa deberá imprimir las ecuaciones solicitas en dos líneas usando el formato de ejemplo. Los valores que calcules para h, k, r, c, d, y e de las ecuaciones (1) y (2) deberán ser impresos con tres dígitos después del punto decimal. Los signos de suma y resta de las ecuaciones deberán ser cambiados según convenga para evitar tener más de un signo delante de un número. Los signos de suma, resta e igualdad deberán estar separados de los caracteres adyacentes por un solo espacio en blanco en ambos lados. No deberán haber otros espacios en blanco en las ecuaciones. Imprime una línea en blanco después de cada par de ecuaciones.
Solución: Nos piden que busquemos un círculo que pase por tres puntos en el plano. Si consideramos a estos puntos como los vértices de un triángulo, necesitamos encontrar su circuncírculo. Para obtenerlo, vamos a sacar la mediatriz de dos lados y revisar donde se intersectan (no necesitamos obtener la mediatriz del tercero, ya que las tres se intersectan en el mismo punto).
La mediatriz de un lado del triángulo es la recta que pasa por su punto medio y es perpendicular (u ortogonal) al mismo. Cuando dos líneas son perpendiculares, sus pendientes son recíprocas y de signo contrario. Teniendo un punto y la pendiente de las dos mediatrices, podemos obtener donde se intersectan utilizando un enfoque similar al de la sección 7.3.
Las variables h y k van a ser las coordenadas del punto de intersección, para obtener r, calculamos la distancia del centro a cualquiera de los vértices.
Para obtener la segunda ecuación, hacemos lo siguiente:
(x -h)2 + (y –k)2 = r2
(x2 -2xh + h2) + (y2 -2yk + k2) = r2
x2 + y2 -2xh -2yk + h2 + k2 –r2 = 0
Por lo que:
c = -2h
d = -2k
e = h2 + k2 –r2
Otra forma para encontrar la solución (y que se pudiera considerar más elegante, aunque no la vamos a implementar), es resolviendo la siguiente determinante:
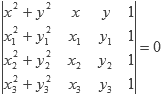
Donde (x1, y1), (x2, y2) y (x3, y3) son los vértices del triángulo.
Código
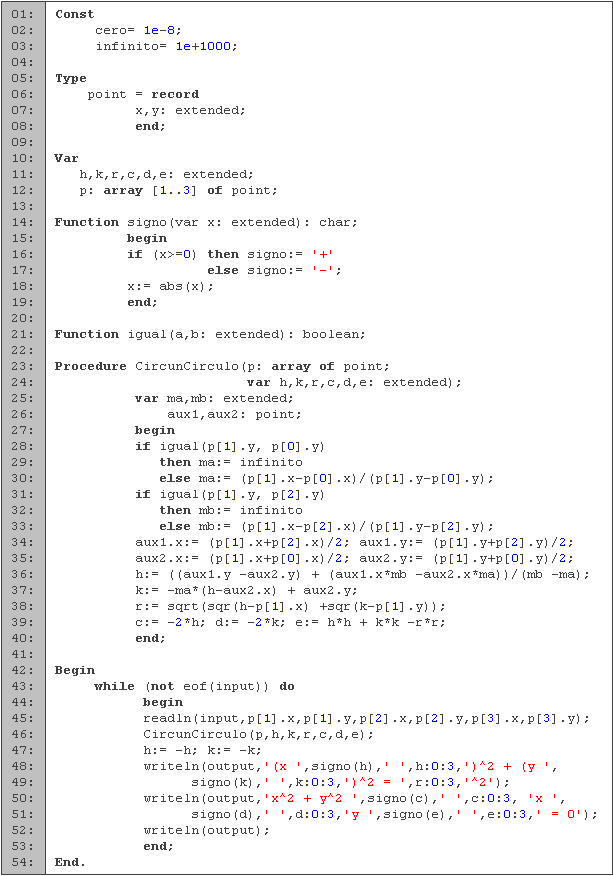
En las primeras tres líneas definimos la constante para infinito, que la vamos a utilizar para las pendientes, y cero para los errores de tolerancia, al igual que en problemas anteriores. Después definimos la estructura de un punto (líneas 4 a 7). Los puntos los leemos en el arreglo p, y las variables h, k, r, c, d y e las utilizamos de acuerdo a la descripción del problema.
La siguiente función, signo, escribe el signo del parámetro de entrada y después le saca el valor absoluto. La única utilidad de esta función es para hacer más simple la escritura de la salida de acuerdo al formato que nos piden. La función igual determina si dos números flotantes son iguales; es la misma que utilizamos en la sección 7.3.
Después tenemos la función CircunCirculo (líneas 23 a 40), donde encontramos los valores de este círculo. Como variables internas tenemos ma y mb que son las pendientes de las mediatrices, junto con aux1 y aux2 que son los puntos medios. De las líneas 28 a 33 calculamos las pendientes de las mediatrices, y entre las líneas 34 y 35 calculamos los puntos medios. En las líneas 36 y 37 calculamos el punto de intersección de la misma manera que en la sección 7.3, sólo que en este caso no consideramos condiciones especiales. Después calculamos el valor del radio, encontrando la distancia a un vértice (líneas 38). Terminamos en la línea 39 obteniendo los valores que faltan, de acuerdo a las ecuaciones que obtuvimos arriba.
Entre las líneas 42 y 54 tenemos la parte principal del código. Procesamos entradas mientras no lleguemos al fin de archivo (línea 43). Para cada entrada, leemos los tres puntos (línea 45) y calculamos los valores de las constantes de las ecuaciones (línea 46). Después les cambiamos los signos a h y k, ya que en la ecuación aparecen con signo opuestos. Por último, escribimos las dos ecuaciones en una línea cada una y una línea en blanco después.Caso ejemplo
| Entrada: | 7.0 -5.0 -1.0 1.0 0.0 -6.0 |
| Desarrollo: |
ma= (-1 -7)/(1 –(-5)) = (-8)/(6)= -1.3 mb= (-1 -0)/(1 –(-6)) = (-1)/(7)= -0.142857 aux1.x= (-1+0)/2 = -0.5; aux1.y= (1+(-6))/2 = -2.5; aux2.x= (-1+7)/2 = 3; aux2.y= (1+(-5))/2 = -2; h= ((-2.5 –(-2))+(-0.5*(-0.14) –3*(-1.3))/(-0.14-(1-3))= 3 k= -(-1.3)*(3-3) + (-2) = -2 r^2= (3-(-1))^2 + (-2-1)^2 = 16 + 9 = 25; r= 5 c= -(3*2)= -6; d= -(-2*2)= 4; e= 3*3 + (-2*-2) –5*5 = -12; |
| Salida: |
(x - 3.000)^2 + (y + 2.000)^2 = 5.000^2 x^2 + y^2 - 6.000x + 4.000y - 12.000 = 0 |
Nota: Las pendientes no se muestran con todos sus decimales.
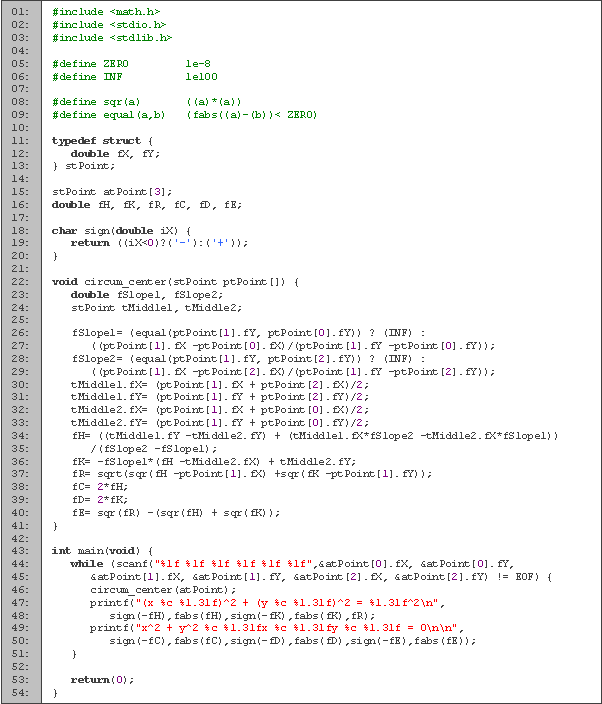
Código en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 04-May-2006 | 0.002 | 0.000 | 0.000 | 7.207 | Minimum |
| C | 15-Jun-2006 | 0.000 | Minimum | |||
Otros problemas
Valladollid:
Zhejiang:
 Intersección recta-segmento y segmento-segmento
Intersección recta-segmento y segmento-segmento
