Teniendo una cantidad ilimitada de monedas de diferentes denominaciones, nos interesa encontrar de cuantas formas se puede pagar una cantidad predeterminada de dinero. Por ejemplo, teniendo monedas de 1, 2 y 5 centavos, podemos formar 6 centavos de la siguientes formas: 6 = 1+1+1+1+1+1 = 1+1+1+1+2 = 1+1+2+2 = 2+2+2 = 1+5.
Si utilizamos la función s(n) para encontrar las formas de pagar n, y utilizamos las denominaciones de las monedas como subíndices, podemos ver que s1,2,5(6) = s1(6-1) + s1,2(6-2) + s1,2,5(6-5) = 1 + 3 + 1 = 5.
En general, para calcular sk1,k2,…,km(n) primero obtenemos sk1,k2,…,km-1(n) y le sumamos sk1,k2,…,km(n-m).
Problema ejemplo
Problema 31
Problema
En Inglaterra la divisa actual está compuesta por la libra esterlina, £, y el penique, p. Existen ocho tipos de monedas en circulación:1p, 2p, 5p, 10p, 20p, 50p, £1 (100p) y £2 (200p).
Es posible hacer £2 de la siguiente forma:
1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p
¿De cuantas formas se pueden formar £2 usando cualquier cantidad de monedas?
Solución: Utilizamos la relación anterior para encontrar las diferentes formas de lograr £2 con las monedas que nos proporcionan.
Código
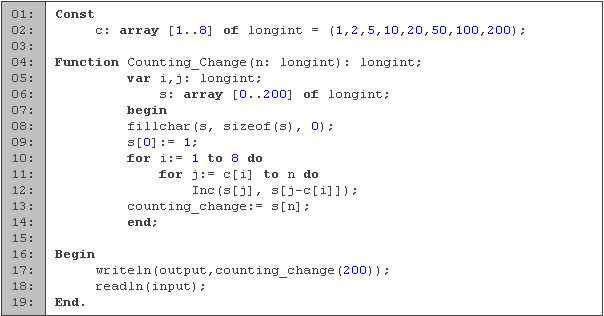
En el primer par de líneas tenemos un arreglo de enteros en el cual guardamos los valores de las distintas monedas. Los valores de las monedas están ordenados, aunque el algoritmo funciona correctamente si no lo estuvieran.
Entre las líneas 4 y 14 tenemos la función que calcula la cantidad de formas distintas en que podemos generar la suma de dinero n. Como variables tenemos i y j para los ciclos y s para guardar las distintas formas de cambio. Empezamos inicializando todos los valores a cero (línea 8), excepto para s(0) que lo inicializamos a 1 (línea 9). La utilidad de hacer s(0) = 1 es que si queremos calcular valores como sk(k), tendríamos que sk(k) = sk(k-k) = 1. Para cada moneda (línea 10), recorremos el arreglo actualizando la cantidad de formas de pago, utilizando la nueva moneda. Es importante empezar desde c[i] para evitar salirnos del arreglo. Al final, devolvemos las distintas formas de pagar n (línea 13).
Caso ejemplo
| Entrada: | 15p |
| Desarrollo: |
s[] 1: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2: 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 5: 1 2 2 3 4 5 6 7 8 10 11 13 14 16 18 10: 1 2 2 3 4 5 6 7 8 11 12 15 16 19 22 |
| Salida: | 22 |
Código en C
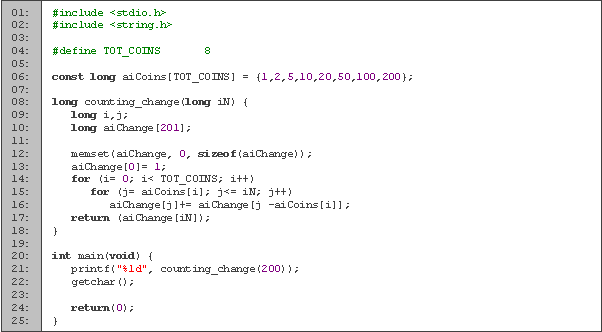
Otros problemas
Valladolid:
 La mochila cero-uno
La mochila cero-uno
