La partición de un número entero es la forma de descomponerlo en forma de suma, con uno o más sumandos positivos (a los que se les conoce como partes). La permutación de sumandos se considera la misma partición. Por ejemplo, el número 4 tiene particiones: 4, 3+1, 2+2, 2+1+1 y 1+1+1+1.

A la función que da como resultado la cantidad de particiones para un número n se le conoce como función partición y está representado por P(n). Por convención, P(0) = 1 y P(n) = 0 para n < 0.

Esta función es muy similar a la del cambio, sólo que podemos considerar que tenemos monedas de denominaciones entre 1 y n. Entonces, utilizando la función P(n, k) como la función partición utilizando particiones menores o iguales a k, podemos calcular P(n, k) obteniendo primero P(n, k-1) y sumándole P(n –k, k).

Cuando a la permutación de sumandos se les considerar un resultado distinto, se le conoce como composición de enteros. Y cuando se permite utilizar el número cero en la composición, a veces se le llama composición débil. Por ejemplo, el número 4 tiene 8 composiciones: 4, 3+1, 2+2, 2+1+1, 1+3, 1+2+1, 1+1+2, 1+1+1+1. La cantidad de composiciones para un número está dada por 2^n-1 para n ≥ 1; y al igual que con la partición, por convención existe una composición para el cero y ninguna para números negativos.




Solución: Utilizamos un algoritmo prácticamente igual al del problema anterior, sólo debemos ajustar la relación a la que acabamos de obtener.




La única variable que vamos a utilizar es n, que es el precio del pastel (líneas 1 y 2).

En la función particion calculamos P(n) (líneas 4 a 14). Las variables i y j las utilizamos en los ciclos, y el arreglo p lo usamos para guardar los valores de la función partición. Inicializamos todos los valores de p a cero, con excepción del valor en la casilla cero que la igualamos a uno (líneas 8 y 9). Después utilizamos la relación que obtuvimos para ir calculando los valores de p (donde i toma los valores de k y j los de n). Terminamos devolviendo las formas en que podemos partir n.

En la parte principal del código (líneas 16 a 19), simplemente leemos n y escribimos P(n).

Entrada:	7
Desarrollo:	p[] 1: 1  1  1  1  1  1  1 2: 1  2  2  3  3  4  4 3: 1  2  3  4  5  7  8 4: 1  2  3  5  6  9 11 5: 1  2  3  5  7 10 13 6: 1  2  3  5  7 11 14 7: 1  2  3  5  7 11 15
Salida:	15

Podemos obtener un algoritmo más eficiente utilizando la siguiente función generadora, atribuida a Euler:

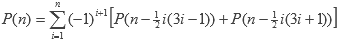
Cuando el valor de 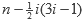 se vuelve menor que uno, entonces todos los valores P son cero. El valor de i a partir del cual P devuelve cero es: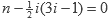

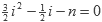
Cuyas soluciones son:

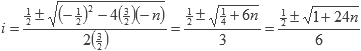
Como i sólo toma valores enteros positivos, tenemos:

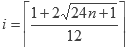
Como dato interesante, la función está relacionada con los números pentagonales, los cuales son de la forma .


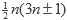El uso de las variables es el mismo que en el problema anterior, y añadimos las variables x e y para guardar valores temporales. El arreglo p tiene una casilla más (la menos uno) para poder manejar valores negativos. Empezamos inicializando las variables (líneas 5 y 6). Entre las líneas 7 y 16 calculamos el valor de P(n) de acuerdo a al función anterior. Las únicas consideraciones que debemos tomar son que el valor hasta que llega j es ligeramente mayor al que calculamos (línea 8) y que para valores negativos P(n) devuelve el mismo resultado (líneas 12 y 13).

Al utilizar esta fórmula, hemos mejorado el tiempo de ejecución de O(n²) a O(n^1.5).

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	28-Abr-2006	0.010	0.010	-	-	100
C	28-Abr-2006	0.010				111
Pascal	28-Abr-2006	0.010				195
C	28-Abr-2006	0.010				198

Project Euler: