En muchos problemas la única forma para encontrar una solución óptima es buscando entre todas las posibles soluciones. A esto se le conoce como búsqueda exhaustiva (o fuerza bruta).

Una búsqueda se puede representar como un recorrido dentro de un árbol. Empezamos desde un punto inicial (la raíz) y a partir de aquí vamos ramificando a todas las posibles alternativas que tenemos. Si en el vértice al que llegamos se encuentra la respuesta, terminamos de buscar; en caso contrario, seguimos ramificando.

Un árbol es una gráfica acíclica y conexa (ver sección 10.1), dicho de otra forma, es una forma de representar la conexión entre objetos relacionados, donde a los objetos los representamos a través de vértices, siempre existe forma de llegar a un vértice desde la raíz y esta es única.

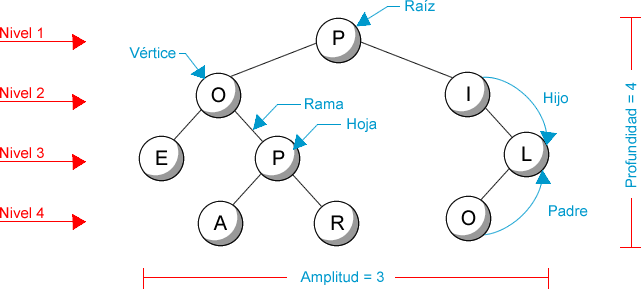Figura 9.1: Ejemplo y terminología de un árbol

A la unión entre dos vértices (o nodos) se le conoce como rama (o arista, si lo consideramos como una gráfica). Cuando dos vértices están conectados por una rama, al de menor nivel se le llama padre (o antecesor) y al de mayor hijo (o sucesor). Si un vértice no tiene hijos se le llama hoja, y si no tiene padre, raíz. Denominamos nivel a la cantidad de vértices que existen entre la raíz y un vértice seleccionado (incluyendo estos dos). A la cantidad de niveles en el árbol se conoce como profundidad (o altura), y a la cantidad máxima de vértices que encontramos en cualquier nivel se llama amplitud (o anchura). Cuando las ramas de un árbol sólo pueden recorrerse en una dirección, se conoce como arborescencia.

Cuando cada vértice tiene a lo más dos hijos, se le conoce como árbol binario (sección 11.5), y si cada nivel está completo, excepto posiblemente el último, se conoce como montículo (sección 3.4). Si tenemos un conjunto de árboles, se le conoce como bosque.

Existen diversas formas de recorrer un árbol, las cuales difieren en los criterios de decisión sobre cual vértice tomar. Cuando no contamos con información respecto al árbol que vamos a recorrer más que la necesaria para saber si la respuesta es correcta, las búsquedas más utilizadas son las llamadas en amplitud y en profundidad.



Una búsqueda en profundidad la realizamos yendo al primer vértice hijo que encontremos. Repetimos esto hasta llegar al vértice con la respuesta o a una hoja. En caso de que encontremos la respuesta, paramos; en caso de que lleguemos a una hoja, regresamos un nivel y buscamos en los vértices que no hayamos visitado. Para saber como regresarnos, los vértices los vamos guardando en una pila (sección 11.4). Es por esto que se acostumbra programar esta búsqueda de forma recursiva, con lo que el manejo de la pila lo realiza el lenguaje.

Haciendo una búsqueda en profundad del árbol anterior, recorreríamos los vértices en el siguiente orden:

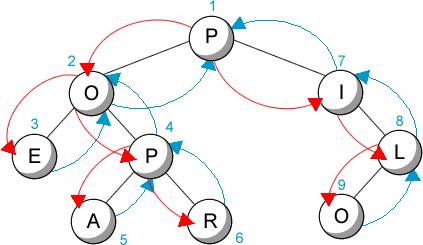Figura 9.2: Búsqueda en profundidad en un árbol

Conociendo el número de ramas (E) y de aristas (V), la complejidad en tiempo de esta búsqueda es de O(E + V). Si denotamos la profundidad máxima como d, y a la cantidad de opciones (ramificaciones) que tenemos en cada vértice como c, entonces la complejidad en tiempo la podemos expresar como O(c^d) y la complejidad en espacio como O(d).

Cuando es utilizada para búsquedas exhaustivas en problemas de cumplimiento de restricciones, a la búsqueda en profundidad también se le conoce como “vuelta atrás” (backtracking). Para acelerar la búsqueda, es común que en los problemas de vuelta atrás se revise si al visitar un nuevo vértice se siguen cumpliendo las condiciones de restricción. Con esto podemos evitar tener que llegar hasta una hoja para saber si el problema está resuelto. También se acostumbra utilizar las variables con más restricciones al principio, ya que generalmente ayuda a visitar menos vértices.



En esta búsqueda, visitamos todos los vértices de un nivel antes de pasar al siguiente. Una vez que encontramos la respuesta, nos detenemos. Para poder saber que vértices visitar, utilizamos una cola (sección 11.4). El siguiente vértice a visitar es el primero de la cola, y una vez visitado, lo quitamos de la cola y agregamos a sus hijos al final.

Utilizando el mismo árbol, la búsqueda sería la siguiente:

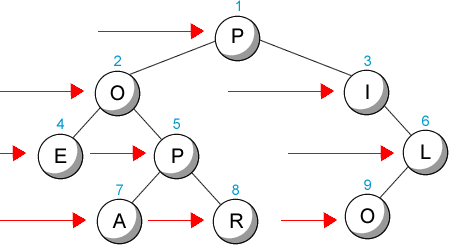Figura 9.3: Búsqueda en amplitud en un árbol

La complejidad tanto en tiempo como en memoria de esta búsqueda es de O(E + V). Utilizando a l como el nivel en el que encontramos la solución y a c como la cantidad de opciones que tenemos en cada vértice, la complejidad en tiempo y memoria es de O(c^l).