Decimos que una fracción es irreducible (o irreductible) cuando el nominador y el denominador son primos relativos, esto es, para la fracción
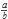 tenemos que mcd(a,b) = 1. Decimos que una fracción es propia cuando su valor es menor a 1 (
tenemos que mcd(a,b) = 1. Decimos que una fracción es propia cuando su valor es menor a 1 (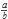 < 1).
< 1).Tenemos que la sucesión de fracciones irreducibles contiene a todas las fracciones irreducibles propias ordenadas de la menor a la mayor. Como la cantidad de fracciones es infinita, se fija un número m al cual el denominador no puede exceder.
A esta sucesión se le conoce como la sucesión de Farey, en honor a John Farey, quien publicó una conjetura de como generarla en 1816. Tiempo después, Cauchy demostró el método de Farey, y desde entonces lleva su nombre. Algo interesante es que Haros ya había demostrado y publicado esta sucesión en 1802, aunque pasó desapercibida.
Para encontrar la sucesión, empezamos con los valores de los extremos (
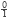 y
y 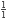 ). Para obtener un nuevo término
). Para obtener un nuevo término 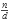 , que se encuentra entre las fracciones
, que se encuentra entre las fracciones 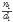 y
y 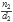 sólo tenemos que hacer
sólo tenemos que hacer 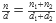 , y revisar que d ≤ n.
, y revisar que d ≤ n.Si estructuramos en forma de árbol binario (sección 11.6) a las fracciones irreducibles (tanto propias como impropias), utilizando la fórmula anterior, obtendríamos la siguiente representación:
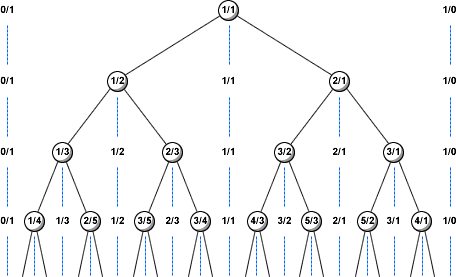 |
| Figura 9.4: Árbol Stern-Brocot |
A este árbol se le conoce como árbol Stern-Brocot, y podemos encontrar la sucesión de Farey en la parte inferior. Para escribir la sucesión de Farey, sólo necesitamos realizar un recorrido en profundidad en orden (consideramos primero el hijo izquierdo, luego el vértice y por último el hijo derecho), donde la profundidad de la búsqueda está dada por el valor máximo del denominador.
Dentro del árbol Stern-Brocot, también podemos encontrar la representación en fracciones continuas de cualquier fracción irreducible. Empezando en la raíz (
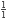 ), contamos cuantas veces nos movemos hacia la derecha y hacia la izquierda alternadamente, y al la última cuenta le añadimos uno. Por ejemplo, para representar
), contamos cuantas veces nos movemos hacia la derecha y hacia la izquierda alternadamente, y al la última cuenta le añadimos uno. Por ejemplo, para representar 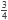 como fracción continua, primero nos movemos 0 veces a la derecha, luego 1 a la izquierda y después 2 a la derecha. Por lo tanto,
como fracción continua, primero nos movemos 0 veces a la derecha, luego 1 a la izquierda y después 2 a la derecha. Por lo tanto, 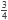 = [0; 1,2+1]:
= [0; 1,2+1]: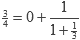
Además podemos visualizar la sucesión de Farey a través de los círculos de Ford. Las fracciones irreducibles
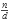 , las graficamos utilizando la ecuación:
, las graficamos utilizando la ecuación: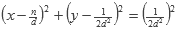
Los círculos que son tangentes corresponden a las fracciones que son consecutivas en la sucesión. Los demás círculos no se intersectan.
Problema ejemplo
Problema 73
Problema
Considera la fracción 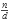 , donde n y d son enteros positivos. Si n < d y mcd(n, d) = 1, se le conoce como fracción propia irreducible.
, donde n y d son enteros positivos. Si n < d y mcd(n, d) = 1, se le conoce como fracción propia irreducible.Si ponemos en una lista todas las fracciones propias irreducibles para la cuales d ≤ 8 en orden ascendente, obtenemos:
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
Podemos ver que existen tres fracciones entre 1/3 y 1/2.
¿Cuántas fracciones hay entre 1/3 y 1/2 en el conjunto ordenado de fracciones propias irreducibles para d ≤ 10,000?
Solución: La sucesión que nos presentan es la de Farey. Para contar cuantas fracciones existen entre
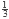 y
y 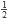 , recorremos el árbol Stern-Brocot, y agregamos una condición para que cuente una vez que llegue a
, recorremos el árbol Stern-Brocot, y agregamos una condición para que cuente una vez que llegue a 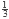 y que termine de ejecutarse cuando llegue a
y que termine de ejecutarse cuando llegue a 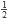 .
.Código

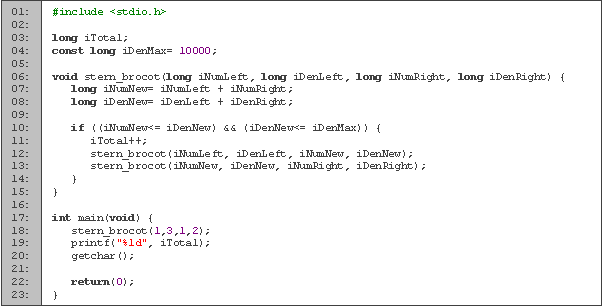
Entre las líneas 1 y 3 tenemos la declaración de variables. La variable b la utilizamos para saber cuando empezamos a contar, r para contar y d que índica el valor máximo del denominador (10000).
En el procedimiento stern_brocot recorremos la sucesión a partir del árbol (líneas 5 a 17). Empezamos calculando la fracción que está entre las dos anteriores (línea 8). Si el denominador no excede al límite, lo tomamos como un vértice válido. A partir de este vértice, ramificamos a sus dos hijos (líneas 11 y 15), y en medio revisamos si estamos en el intervalo y en caso de estar, incrementamos nuestra cuenta. Cuando llegamos a un medio, nos salimos.
Posibles Cambios
Observando el árbol, podemos notar que
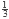 es hijo de
es hijo de 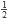 , por lo que las fracciones entre
, por lo que las fracciones entre 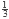 y
y 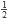 son aquellas que se encuentran a partir de la rama derecha del primero. Aprovechando esto, podríamos empezar la función stern_brocot con estas dos fracciones como parámetros (en la línea 21), con lo que ya no necesitaríamos las líneas 12 y 14 además de que recorreríamos menos de la mitad de los valores. Otra mejora que podemos hacer, aunque menos significativa, es sólo calcular los valores de denominadores, ya que el de los nominadores no los utilizamos.
son aquellas que se encuentran a partir de la rama derecha del primero. Aprovechando esto, podríamos empezar la función stern_brocot con estas dos fracciones como parámetros (en la línea 21), con lo que ya no necesitaríamos las líneas 12 y 14 además de que recorreríamos menos de la mitad de los valores. Otra mejora que podemos hacer, aunque menos significativa, es sólo calcular los valores de denominadores, ya que el de los nominadores no los utilizamos.Caso ejemplo
| Entrada: | 8 |
| Desarrollo: |
n1/d1 n2/d2; an/ad; r b 0/1 1/1 ; 1/2 ; 0 FALSE 0/1 1/2 ; 1/3 ; 0 FALSE 0/1 1/3 ; 1/4 ; 0 FALSE 0/1 1/4 ; 1/5 ; 0 FALSE 0/1 1/5 ; 1/6 ; 0 FALSE 0/1 1/6 ; 1/7 ; 0 FALSE 0/1 1/7 ; 1/8 ; 0 FALSE 0/1 1/8 ; 1/9 ; 0 FALSE 1/8 1/7 ; 2/15; 0 FALSE 1/7 1/6 ; 2/13; 0 FALSE 1/6 1/5 ; 2/11; 0 FALSE 1/5 1/4 ; 2/9 ; 0 FALSE 1/4 1/3 ; 2/7 ; 0 FALSE 1/4 2/7 ; 3/11; 0 FALSE 2/7 1/3 ; 3/10; 0 FALSE 1/3 1/2 ; 2/5 ; 0 TRUE 1/3 2/5 ; 3/8 ; 0 TRUE 1/3 3/8 ; 4/11; 0 TRUE 3/8 2/5 ; 5/13; 1 TRUE 2/5 1/2 ; 3/7 ; 2 TRUE 2/5 3/7 ; 5/12; 2 TRUE 3/7 1/2 ; 4/9 ; 3 TRUE |
| Salida: | 3 |
Código en C
 Introducción
Introducción
