Teniendo una gráfica, queremos encontrar o recorrer sus componentes conexas. Por ejemplo, suponiendo que los vértices en una gráfica representan países, y que las aristas unen a países del mismo continente que tienen frontera común, nos puede interesar saber cuantos continentes existen, saber cual continente tiene más países o asignarle alguna etiqueta a cada país.
Para encontrar las componentes conexas, primero marcamos todos los vértices como no visitados, y después elegimos al primero de ellos. A este vértice lo marcamos como perteneciente a la primera componente, y después marcamos a todos los que están conectados con el, y repetimos esto hasta que no encontremos algún vértice adyacente. En seguida, buscamos algún vértice que no haya sido visitado, lo marcamos como perteneciente a la segunda componte y marcamos todos los que estén interconectados. Esto lo repetimos hasta que ya no existan vértices sin marcar.
Para hacerlo de forma sistemática, podemos buscar cuales vértices no han sido marcados mediante una búsqueda lineal (con un for, por ejemplo) y cada ocasión que encontremos alguno, realizamos una búsqueda en profundidad. Podemos cambiar la búsqueda en profundidad por cualquier otra búsqueda exhaustiva en un árbol, pero generalmente es más sencillo de programar la primera.
Podemos imaginar el funcionamiento de este algoritmo como cuando utilizamos la cubeta en algún programa de dibujo (diseño). Empezamos en un punto predeterminado, y a partir de ahí nos expandemos coloreando todo hasta que lleguemos a los bordes de la imagen.
Problema ejemplo
Laberinto
Problema
La administración del laberinto ha decidido empezar una nueva temporada con un papel tapiz nuevo. Para esto, necesitan un programa que calcule cuantos cuadros tiene el laberinto. ¡Es un trabajo justo para ti!El laberinto está representado por una matriz de n×n (3 ≤ n ≤ 33, ya que ¡‘3’ es un dígito mágico!). Algunas celdas de la matriz tienen un caracter de punto (‘.’) que denota a un cuadro vacío. Otras celdas contienen un caracter de numeral (‘#’) que denota un cuadro en el cual hay un monolito de piedra. Todos los cuadros son de tamaño 3×3 metros.
Se construyeron paredes alrededor del laberinto (excepto por las esquinas superior izquierda e inferior derecha, las cuales son usadas como entradas y alrededor de las celdas con caracter de numeral. No se construyeron otras paredes. Siempre habrá un caracter de punto en las celdas superior izquierda e inferior derecha de la matriz de entrada.
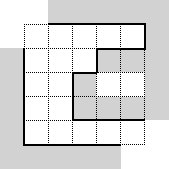
Tu trabajo es calcular la cantidad de cuadros visibles en las paredes dentro del laberinto. En otras palabras, la cantidad de superficie visible para un visitante dentro del laberinto. Debes tener en cuenta que no hay hoyos por lo cuales ver, y no te puedes mover entre dos bloques de piedra adyacentes. Dos bloques se consideran adyacentes si se tocan en cualquiera de sus esquinas. Tomando por ejemplo la imagen: las paredes visibles dentro del laberinto son las que tienen las líneas marcadas en negro. La altura de todas las paredes es de tres metros.
Entrada
La primera línea de la entrada contiene un entero n. Las siguientes n líneas contienen n caracteres cada una. Cada línea describe una fila de la matriz del laberinto. En cada línea solo habrá caracteres de punto y numeral, y será finalizada con un caracter de fin de línea. No hay espacios en la entrada.Salida
Tu programa deberá escribir en la salida un solo entero: la cantidad exacta de cuadros de papel tapiz que se necesitan.Solución: Recorremos todos los cuartos y cada que encontremos una pared, incrementamos un contador. El recorrido lo vamos a realizar mediante una búsqueda en profundidad. Un detalle que debemos considerar es que en el problema no se especifica si las dos entradas (las esquinas) están conectadas, por lo que existe la posibilidad de que existan dos componentes conexas distintas.
Código

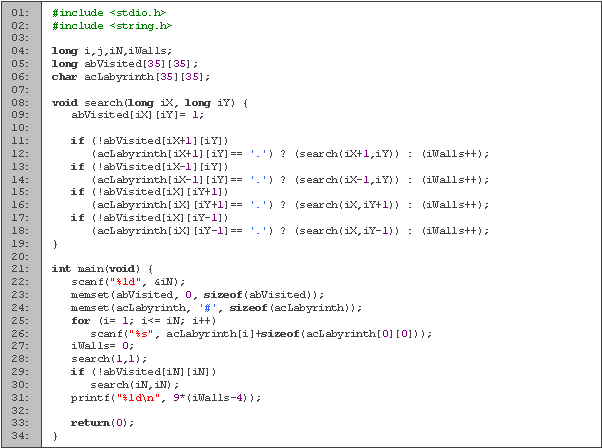
En las primeras cuatro líneas declaramos las variables a utilizar. Las variables i y j las utilizamos para los ciclos, n para el tamaño del laberinto, t para contar el total de paredes, l para guardar el laberinto y b para saber si ya visitamos un cuarto. Para no tener que revisar los casos especiales de las orillas, agregamos un contorno extra a los arreglos (comúnmente llamados “centinelas”).
En el procedimiento recorre (líneas 6 a la 21), visitamos el laberinto. Empezamos poniendo el cuarto actual como recorrido (línea 8). En las siguientes tres líneas revisamos si el cuarto a la derecha lo hemos visitado, y si no lo hemos hecho, revisamos si es un cuarto vacío o una pared. En el caso de que sea un cuarto, lo visitamos. En el caso de que sea una pared, la contamos. En las siguientes nueve líneas realizamos lo mismo que en las tres anteriores, pero para los cuartos de la izquierda, arriba y abajo.
Caso ejemplo
| Entrada: |
5 ..... ...## ..#.. ..### ..... |
| Desarrollo: |
x y paredes 1 1; 2 2 1; 3 3 1; 4 4 1; 5 5 1; 7 5 2; 8 4 2; 9 3 2; 10 2 2; 10 1 2; 11 1 3; 12 2 3; 14 1 4; 16 1 5; 19 5 3; 21 5 4; 23 5 5; 26 9*(26-5)= 198 |
| Salida: | 198 |
Nota: En este ejemplo estamos contando las paredes al momento de entrar en el cuadro en lugar de cuando intentamos acceder a otro, por lo que los valores no corresponden a los de la variable t.
Código en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 26-Abr-2006 | 0.001 | 0.001 | 0.015 | 0.125 | 142 |
| C | 27-Abr-2006 | 0.001 | 146 | |||
Otros problemas
Valladolid:
260 - Il Gioco dell'X
352 - The Seasonal War
469 - Wetlands of Florida
572 - Oil Deposits
657 - The die is cast
705 - Slash Maze
776 - Monkeys in a Regular Forest
782 - Contour Painting
784 - Maze Exploration
785 - Grid Colouring
830 - Shark
852 - Deciding victory in Go
871 - Counting Cells in a Blob
10279 - Mine Sweeper
10336 - Rank the Languages
10344 - 23 out of 5
10592 - Freedom Fighter
10946 - You want what filled?
352 - The Seasonal War
469 - Wetlands of Florida
572 - Oil Deposits
657 - The die is cast
705 - Slash Maze
776 - Monkeys in a Regular Forest
782 - Contour Painting
784 - Maze Exploration
785 - Grid Colouring
830 - Shark
852 - Deciding victory in Go
871 - Counting Cells in a Blob
10279 - Mine Sweeper
10336 - Rank the Languages
10344 - 23 out of 5
10592 - Freedom Fighter
10946 - You want what filled?
 Sucesión de Farey y árbol Stern-Brocot
Sucesión de Farey y árbol Stern-Brocot
