Este es un problema muy recurrido al estudiar algoritmos, por lo que se puede encontrar en muchos libros. La versión original del problema busca las formas en que se puede acomodar en un tablero de ajedrez (un tablero de 8×8 casillas) a 8 reinas, de tal forma que ninguna de las reinas esté en posición de ataque. Una reina puede atacar a otra pieza de ajedrez cuando se encuentra en el mismo renglón, columna o diagonal. Una de la variantes más comunes del problema es poner n reinas en un tablero de n×n.
El problema de las 8 reinas cuenta con 92 soluciones distintas, pero si consideramos que las soluciones que difieren sólo por rotaciones o reflexiones son iguales, entonces sólo cuenta con 12 soluciones únicas. Para los primeros valores de n tenemos:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Únicas | 1 | 0 | 0 | 1 | 2 | 1 | 6 | 12 | 46 | 92 | 341 | 1787 |
| Distintas | 1 | 0 | 0 | 2 | 10 | 4 | 40 | 92 | 352 | 724 | 2680 | 14200 |
No intentes escribir un programa que evalúe todas las 8 posibles posiciones de las 8 reinas en el tablero. Esto requeriría 88 evaluaciones y saturaría el sistema. Habrá un tiempo límite razonable para que corra tu programa.
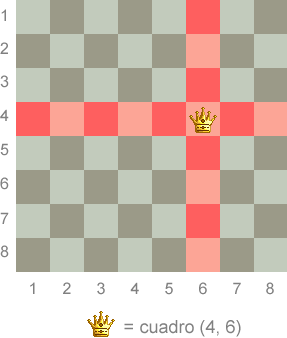
Para estandarizar la notación, asumiremos que la esquina superior izquierda del tablero ocupa la posición (1, 1). Las filas van a lo horizontal y la que se encuentra arriba es la fila 1. Las columnas van en vertical y la columna que esta a la izquierda es la 1. Cualquier referencia a un cuadro se hace primero por fila y después columna; por lo tanto (4, 6) se refiere a la fila 4, columna 6.
Cada caso está separado por una línea en blanco.
Cada solución deberá estar numerada secuencialmente de 1 a n. Cada solución contendrá 8 números. Cada uno de los 8 números será la coordenada de la fila de la solución. La coordenada de la columna estará dada por el orden en que los 8 números están impresos. Esto es, el primer número representa la fila en el que está la reina de la primera columna; el segundo número representa la fila en el que está la reina de la segunda columna; y así sucesivamente.
Cada solución deberá estar en una solo línea, con la representación de 8 dígitos que se acaba de mencionar.
Incluye las dos líneas de encabezado que se muestran en la salida del ejemplo e imprime las soluciones en orden lexicográfico.
Imprime una línea en blanco entre cada caso.
Solución: Sabemos que sólo existen 92 soluciones, por lo que vamos a generarlas primero y en cada caso imprimimos las que tengan una reina en la casilla que nos piden. Para encontrar las soluciones, vamos ir poniendo una reina por cada columna, revisando que no entre en conflicto con las reinas anteriores. Si ya colocamos la ocho, o a la reina actual no la podemos colocar sin atacar a alguna otra, nos regresamos y cambiamos de casilla a la anterior. Cada vez que hayamos puesto todas, guardamos la solución.
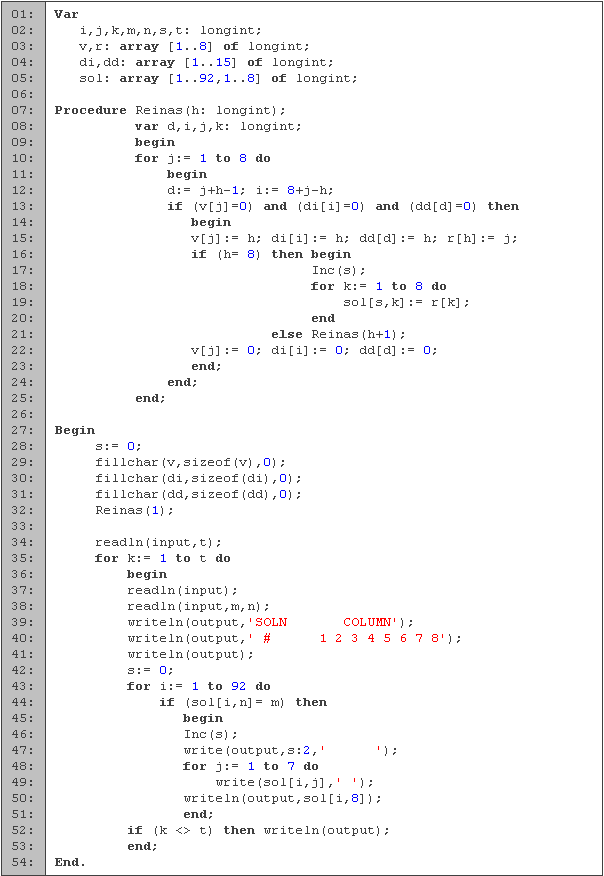
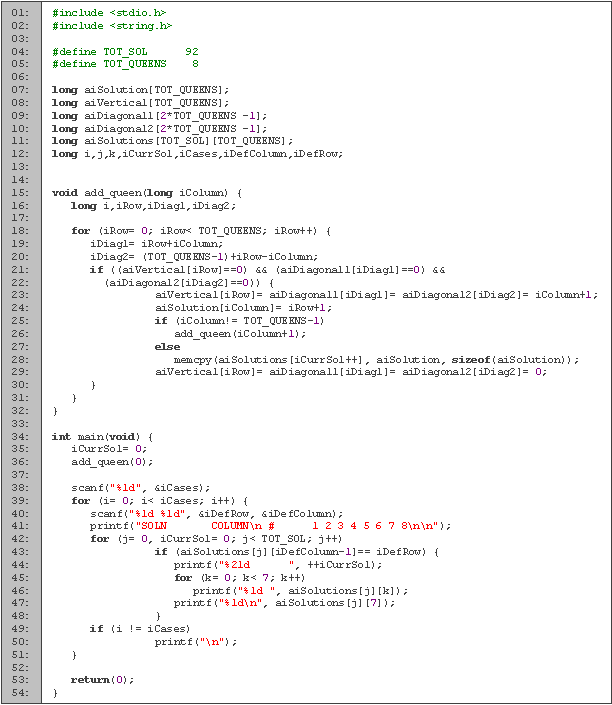
En las primeras cinco líneas de código tenemos la declaración de variables. Para los ciclos utilizamos las variables i, j y k, s para llevar la cuenta de las soluciones, m y n para saber la posición de la reina que está fija, y t para leer el número de casos. Para saber cuales posiciones están en ataque, en lugar de utilizar un matriz para representar el tablero, vamos a utilizar tres arreglos (v, di, dd) para saber si las columnas o las diagonales están en ataque. En el arreglo r guardamos la solución actual y en sol todas las soluciones.
Las soluciones las generamos en el procedimiento reinas (líneas 7 a 25). Tenemos como parámetro h, que nos indica en cual renglón vamos a poner la reina. Como ponemos una reina por renglón, el número de renglón también nos indica cuantas reinas ya colocamos. Para cada una de las casillas en este renglón (línea 10), intentamos poner la reina con la condición de que no sea atacada por las anteriores (línea 13). Para saber cuales diagonales están siendo atacadas, utilizamos las variables d e i (línea 12) para las dos diagonales y j para las columnas.
Sabiendo que la casilla no está siendo atacada, ponemos a la reina actual ahí. Esto lo hacemos anotando la reina que estamos utilizando en los valores de las diagonales y la columna, y guardando este valor en la solución actual (línea 15). Para el uso que les estamos dando, los arreglos v, di, dd pudieran ser booleanos, pero saber que reina está atacando estas posiciones pudiera ser interesante en otros problemas.
Si ya colocamos todas las reinas, guardamos la solución actual (líneas 16 a 20); en caso de que todavía falten, ponemos la siguiente (línea 21). Al regresar de la recursividad, quitamos los valores que habíamos asignado (línea 22). No borramos el valor de la solución (r[h]), ya que no lo usamos para saber si una reina se puede poner, y al momento de agregar otra, este valor será sobrescrito. Contando las veces que se llama esta función, podemos ver como al revisar antes de poner a las reinas reducimos la cantidad de vértices visitados de 88 a sólo 1965.
| Entrada: |
1 1 2 |
| Desarrollo: |
h v di dd 0; 0 0 0 0; 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 1; 1 0 0 0; 0 0 0 1 0 0 0; 1 0 0 0 0 0 0 2; 1 0 2 0; 0 0 0 1 2 0 0; 1 0 0 2 0 0 0 2; 1 0 0 2; 0 0 0 1 0 2 0; 1 0 0 0 2 0 0 3; 1 3 0 2; 0 0 3 1 0 2 0; 1 0 0 3 2 0 0 1; 0 1 0 0; 0 0 0 0 1 0 0; 0 1 0 0 0 0 0 2; 0 1 0 2; 0 0 0 0 1 2 0; 0 1 0 0 2 0 0 3; 3 1 0 2; 0 3 0 0 1 2 0; 0 1 3 0 2 0 0 4; 3 1 4 2; 0 3 4 0 1 2 0; 0 1 3 0 2 4 0 ← 1; 0 0 1 0; 0 0 0 0 0 1 0; 0 0 1 0 0 0 0 2; 2 0 1 0; 0 0 2 0 0 1 0; 0 2 1 0 0 0 0 3; 2 0 1 3; 0 0 2 0 3 1 0; 0 2 1 0 0 3 0 4; 2 4 1 3; 0 4 2 0 3 1 0; 0 2 1 0 4 3 0 ← 1; 0 0 0 1; 0 0 0 0 0 0 1; 0 0 0 1 0 0 0 2; 2 0 0 1; 0 0 2 0 0 0 1; 0 2 0 1 0 0 0 3; 2 0 3 1; 0 0 2 3 0 0 1; 0 2 0 1 3 0 0 2; 0 2 0 1; 0 0 0 2 0 0 1; 0 0 2 1 0 0 0 |
| Salida: |
SOLN COLUMN # 1 2 3 4 5 6 7 8 1 3 1 4 2 |
Nota: Estamos considerando sólo 4 reinas para poder mostrar todo el procedimiento.
Una forma heurística de encontrar soluciones se puede obtener moviendo la reina que se encuentre en más posiciones de ataque a otra casilla dentro de la misma columna donde existan menos. Este enfoque puede resolver el problema de las reinas para tableros grandes de forma rápida (teniendo una buena aproximación inicial), aunque tiene el inconveniente de que no siempre encuentra solución, ya que existen casos en los que se queda dentro de un ciclo.
También existe un algoritmo con el que podemos encontrar una solución para el problema de la n reinas (con n ≥ 4) de forma casi inmediata. Primero escribimos todos los números pares, seguido por todos los impares (que sean menores a n). Después tomamos el residuo de n entre 12, y dependiendo del resultado tomamos las siguientes consideraciones:
- Si el residuo es 2, cambiamos de lugar el 1 con el 3, y mandamos el 5 al final de la lista.
- Si el residuo es 3 o 9, entonces movemos el 2 al final de los pares, y movemos el 1 y el 3 al final de la lista.
- Si el residuo es 8, volteamos las parejas de los impares (el 1 con el 3, el 5 con el 7, etc.)
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 27-May-2006 | 0.016 | 0.000 | 0.010 | 3.350 | Minimum |
| C | 29-May-2006 | 0.002 | Minimum | |||
 Podas (Pruning)
Podas (Pruning)
