El Sudoku es un crucigrama que inicialmente fue creado en los Estados Unidos bajo el nombre de “Number Place” a finales de los setenta, pero que ganó gran popularidad en Japón desde mediados de los ochenta y que en épocas recientes se ha extendido al resto del mundo.
El crucigrama se juega en una cuadricula de 9×9, que contiene 9 regiones de tamaño 3×3. El objetivo del juego es colocar todos los números del uno al nueve en cada renglón, columna y región, sin que se repitan en alguna de estas tres secciones, teniendo al principio algunos números ya acomodados. La dificultad del crucigrama varía de acuerdo a la cantidad y posición de estos números iniciales. La generalización de este problema a una cuadrícula de n×n, es NP-completo.
Problema ejemplo
Problema 96
Problema
Su Doku (que en japonés significa literalmente número posición) es el nombre de un rompecabezas popular. Su origen es incierto, pero se le atribuye principalmente a Leonhard Euler quien inventó uno similar y mucho más difícil, conocido como Cuadros Latinos. El objetivo de un rompecabezas Su Doku es reemplazar los espacios en blanco (o ceros) en una cuadrícula de 9 por 9, de tal forma que en cada fila, columna y caja de 3 por 3 solo aparezca una vez cada dígito del 1 al 9. Abajo aparece la forma inicial y la solución para un rompecabezas de este tipo.
|
|
Un Su Doku bien construido tiene solo una solución válida y puede ser resuelto de manera lógica, aunque puede ser necesario utilizar un método de “adivinar y probar” para eliminar algunas opciones (existen opiniones encontradas al respecto). La complejidad de la búsqueda determina la dificultad del rompecabezas; al ejemplo se le considera sencillo porque puede ser resuelto utilizando deducción directa.
El archivo de 6K, sudoku.txt (has click en el botón derecho y oprime “Guardar como...”), contiene cincuenta rompecabezas Su Doku distintos de varios niveles de dificultad, pero con solución única (el primer rompecabezas es el del ejemplo).
Resolviendo los cincuenta rompecabezas, encuentra la suma de los números de tres dígitos que se forman en la parte superior izquierda de cada cuadricula resuelta; por ejemplo, 483 es el número de tres dígitos encontrado en la posición superior izquierda de la solución del ejemplo.
Solución: Resolvemos cada uno de los cincuenta crucigramas, y guardamos la suma de los tres dígitos de la esquina superior izquierda. Para resolver cada crucigrama, utilizamos una metodología similar a la de las ocho reinas, esto es, revisamos casilla por casilla intentando resolver el problema con los dígitos que sobran. Si nos quedamos sin opciones en alguna casilla, nos regresamos a las anteriores e intentamos con otros dígitos no usados.
Código
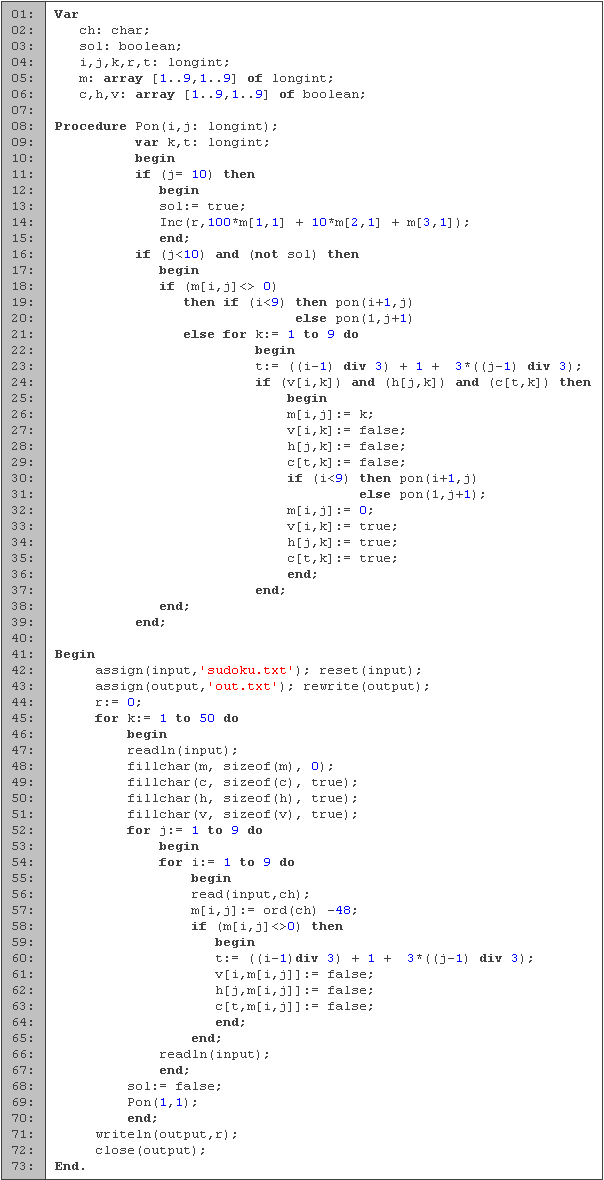
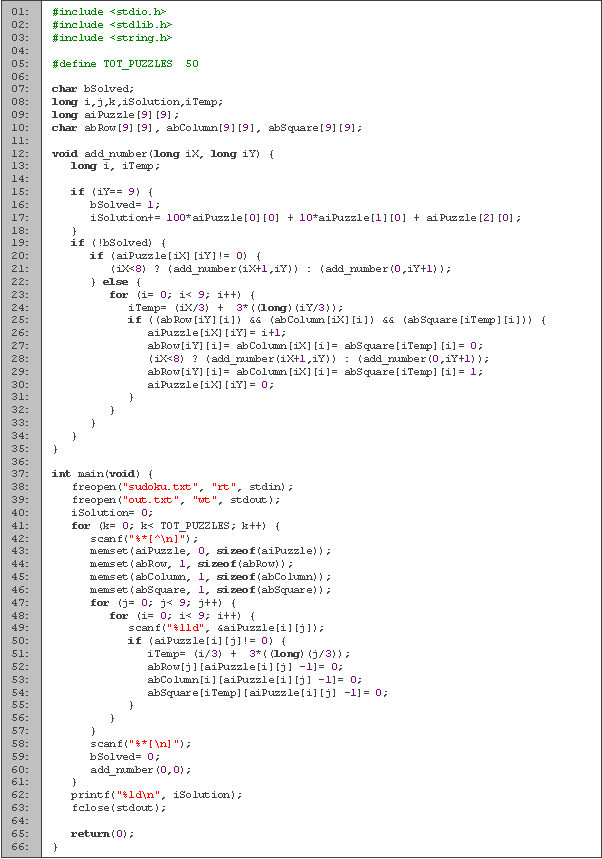
Comenzamos definiendo las variables que vamos a utilizar en las primeras seis líneas. En la matriz m guardamos la solución del Sudoku, y en los arreglos h, v y c guardamos cuales dígitos del renglón, columna y región ya hemos utilizado (podríamos revisarlo en la matriz m, pero con estos arreglos agilizamos el proceso). Los enteros i, j y k los utilizamos para los ciclos, r para guardar el resultado y t para saber en cual región vamos. El booleano sol lo utilizamos para saber cuando ya encontramos la solución (y dejar de recorrer el árbol) y el caracter ch para leer la entrada.
El Sudoku lo resolvemos mediante una búsqueda en profundidad, utilizando el procedimiento pon (líneas 8 a 39), el cuál revisa los dígitos que se pueden poner en la casilla i, j, y cada que encuentra uno, pasa a la siguiente casilla. Al principio revisamos si ya llegamos al resultado, y en caso de que lo hayamos hecho, marcamos la solución como obtenida (línea 13) y guardamos el resultado (línea 14). En caso de que no hayamos llegado al resultado (línea 16), revisamos si ya está ocupada la casilla. Cuando la casilla ya está ocupada, pasamos a la siguiente; cuando no, intentamos poner cada dígito (línea 21). Para revisar la región en la que estamos utilizamos la variable t (línea 23) y las regiones las numeramos de 1 a 9, empezando en la esquina superior derecha y yéndonos de izquierda a derecha y de arriba hacia abajo. Una vez que revisamos que el dígito no ha sido utilizando en el renglón, columna y región, lo ponemos (línea 26), lo marcamos como usado (líneas 27 a 29) y pasamos a la siguiente casilla (líneas 30 y 31). Una vez que regresamos, quitamos los valores que asignamos para intentarlo con un nuevo dígito (líneas 32 a 36).
Caso ejemplo
| Entrada: |
Grid 01 0000 0000 0000 0000 |
| Desarrollo: |
1 1 2 1 3 1 4 1 0000 1000 1200 1230 1234 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 1 2 2 2 3 2 4 2 1234 1234 1234 1234 3000 3400 3410 3412 0000 0000 0000 0000 0000 0000 0000 0000 1 3 2 3 3 3 4 3 1234 1234 1234 1234 3412 3412 3412 3412 2000 2100 2140 2143 0000 0000 0000 0000 1 4 2 4 3 4 4 4 1234 1234 1234 1234 3412 3412 3412 3412 2143 2143 2143 2143 4000 4300 4320 4321 |
| Salida: | 123 |
Nota: Estamos considerando una cuadricula de 4×4, con regiones de 2×2 para poder mostrar todo el procedimiento.
Código en C
El problema de las reinas
