Si lo que queremos es obtener el camino más corto entre todas las pareja posibles, lo primero que se nos puede ocurrir es utilizar el algoritmo de Dijkstra para cada vértice. Sin embargo, podemos encontrar algoritmos más eficientes para este caso.
El algoritmo de Floyd-Warshall (también conocido como algoritmo de Roy-Floyd) aprovecha que los sub-problemas son óptimos, pero desde una perspectiva de programación dinámica.
Este algoritmo se basa en lo siguiente: supongamos que tenemos la forma de llegar del vértice i al j de forma óptima contando con k-1 puntos intermedios. Ahora queremos encontrar la distancia más corta agregando un k-ésimo punto intermedio. Existen dos casos: podemos ir de i a k y después a j, o mantener la distancia de i a j que ya teníamos. En ambos estamos considerando los k -1 puntos como intermedios. Al hacer que k tome el valor de todos los vértices, obtenemos la distancia más corta entre todas las parejas.
Visto como formula, donde dk(i,j) es la distancia mínima para ir de i a j con k puntos, y p(i, j) es el peso de la arista de i a j, tenemos que:
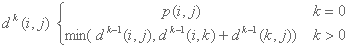
Si además de la distancia, queremos encontrar la trayectoria, podemos hacer algo similar a lo que hicimos con Dijkstra en el problema anterior. La función para imprimir esta trayectoria sería la misma. También podemos encontrar las aristas maxi-min y mini-max utilizando un enfoque parecido al de Dijkstra.
Es común que un jugador empiece una serie de conquistas con el objetivo de transferir parte de su ejército de un país a otro. Normalmente, es conveniente escoger una ruta en la cual la cantidad de países que se tienen que conquistar sea mínima. Dada la descripción de un tablero con 20 países, cada uno con 1 a 19 conexiones a otros países, tu trabajo es escribir un programa que tome un país inicial y uno final, y calcule la cantidad mínima de países que se tienen que conquistar para llegar al destino. Por ejemplo, si el país inicial y el final son vecinos, el programa deber regresar uno.
El siguiente diagrama ilustra la entrada del ejemplo:
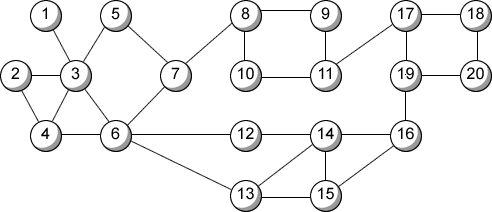
Puede haber varios casos en la entrada; tu programa deberá de ser capaz de leerlos y procesarlos hasta llegar al fin de archivo. Existirá por lo menos una ruta de un país a otro en cualquier configuración dada.
Solución: Como el peso de cada arista es unitario, podemos utilizar una búsqueda en amplitud por cada distancia que nos pidan. Sin embargo, resulta más fácil implementar Floyd, y como la cantidad de vértices son muy pocos la diferencia en tiempo no es significativa.

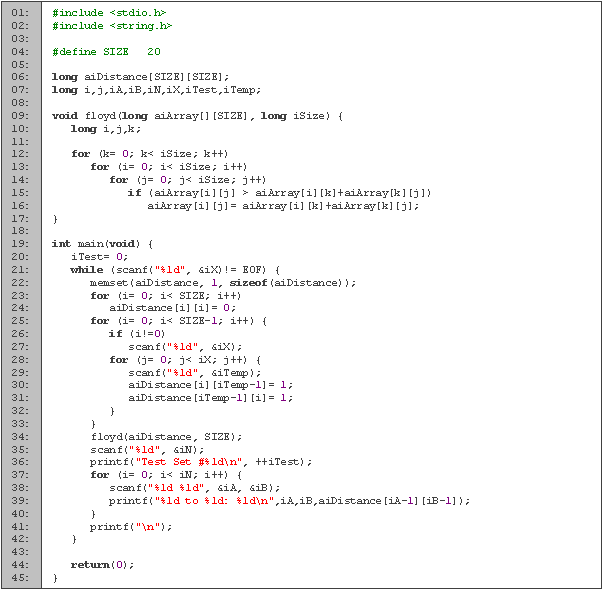
En las primeras tres líneas declaramos las variables que vamos a utilizar. Para los ciclos usamos i y j, para contar en que prueba vamos c, t para leer con que vértice es adyacente el vértice actual, n, x, a, y b las utilizamos de acuerdo a la descripción del problema. La matriz de adyacencia la guardamos en m.
En el procedimiento Floyd (líneas 5 a 13), calculamos la distancia más corta entre todos los pares de vértices. En cada iteración del ciclo k, utilizamos al vértice k como punto intermedio para ir de i a j. Si utilizándolo como punto intermedio logramos llegar más rápido, actualizamos la distancia (línea 12). Una vez que utilizamos a todos los vértices como intermedio, obtenemos las distancias más cortas para cada par de vértices.
Entre las líneas 22 y 31 leemos la conexión entre países. Como los caminos pueden ser transitados en ambas direcciones, asignamos dos valores a la matriz de adyacencia (línea 28). Después utilizamos Floyd para calcular las distancias mínimas (línea 32). Por último, escribimos cual caso estamos procesando (línea 34), leemos las parejas de vértices, y para cada una de ellas, imprimimos la distancia mínima (líneas 38 y 39).
| Entrada: |
3 2 3 4 1 3 1 4 1 5 5 1 4 2 5 3 2 4 3 5 1 |
| Desarrollo: |
m[] 0 1 1 1 ∞ 1 0 1 ∞ ∞ 1 1 0 1 ∞ 1 ∞ 1 0 1 ∞ ∞ ∞ 1 0 k= 1 k= 2 k= 3 k= 4 k= 5 0 1 1 1 ∞ 0 1 1 1 ∞ 0 1 1 1 ∞ 0 1 1 1 2 0 1 1 1 2 1 0 1 2 ∞ 1 0 1 2 ∞ 1 0 1 2 ∞ 1 0 1 2 3 1 0 1 2 3 1 1 0 1 ∞ 1 1 0 1 ∞ 1 1 0 1 ∞ 1 1 0 1 2 1 1 0 1 2 1 2 1 0 1 1 2 1 0 1 1 2 1 0 1 1 2 1 0 1 1 2 1 0 1 ∞ ∞ ∞ 1 0 ∞ ∞ ∞ 1 0 ∞ ∞ ∞ 1 0 2 3 2 1 0 2 3 2 1 0 |
| Salida: |
Test Set #1 1 to 4: 1 2 to 5: 3 3 to 2: 1 4 to 3: 1 5 to 1: 2 |
Nota: Sólo utilizamos 5 vértices para poder mostrar todo el proceso. El signo de infinito tiene un valor de 16843009 durante la ejecución.
Es claro que el tiempo de ejecución de Floyd es de O(V3). Para gráficas dispersas existe un algoritmo conocido como el algoritmo de Johnson, el cual tiene un tiempo de ejecución de O(V2lgV + VE).
El algoritmo de Floyd también puede ser utilizado para encontrar la cerradura transitiva, en cuyo caso se le conoce como el algoritmo de Warshall.. Lo que busca la cerradura transitiva es saber si se puede alcanzar un vértice j a partir del vértice i. Utilizando Floyd, si el camino más corto de i a j es menor a infinito es porque si existe un camino por el que podemos llegar. Sin embargo, podemos hacer algunos cambios para eficientar los cálculos.

Aquí m sigue siendo la matriz de adyacencia pero en lugar de enteros utilizamos booleanos (aunque también funciona con enteros). El vértice j lo podemos alcanzar desde i si ya podíamos llegar desde i hasta j (parte izquierda de la operación), o si podemos llegar desde i a j pasando a través de k (parte derecha).
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 04-May-2006 | 0.010 | 0.000 | 0.000 | 0.050 | 408 |
| C | 04-May-2006 | 0.000 | 392 | |||
Valladolid:
World Archive:
 Camino más corto: Dijkstra
Camino más corto: Dijkstra
