Dada una gráfica, su árbol mínimo generador (o árbol de peso mínimo o árbol mínimo de expansión) es un árbol que pasa por todos los vértices y que la suma de sus aristas es la de menor peso. La forma inmediata en que se nos puede ocurrir para encontrarlo es mediante una búsqueda exhaustiva, sin embargo, podemos encontrarlo más rápido.
De forma similar al problema de la distancia más corta, el árbol mínimo generador puede ser calculado mediante un enfoque ávido. La idea básica es empezar con el árbol vacío e irle agregando una arista a la vez. La arista que escogemos es la de menor costo que no forme un ciclo en nuestro árbol. Después de agregar V-1 aristas, el árbol que tenemos es el árbol mínimo generador. Con esta idea surgen dos algoritmos: Prim y Kruskal, cuya diferencia básica es la forma en que encontremos la arista que vamos a agregar.
El primero que vamos a analizar es Kruskal. En este algoritmo, empezamos considerando cada vértice como un árbol. En cada paso, buscamos la arista de menor peso que no hayamos utilizado y revisamos a que árbol pertenecen los vértices de la arista. Si los dos vértices pertenecen al mismo árbol, entonces no la utilizamos (porque formaría un ciclo); si los vértices pertenecen a árboles distintos, entonces tomamos la arista como parte del árbol mínimo generador y juntamos los dos árboles. Repetimos lo anterior hasta hayamos procesador todas las aristas.
Considera que la espalda de Dick es un plano con varias pecas de coordenadas (x, y). Tu trabajo es decirle a Richie como conectar todas las pecas de forma que utilice la menor cantidad de tinta posible. Richie conecta las pecas utilizando líneas rectas entre los dos puntos, y puede despegar la pluma después de dibujar una línea. Cuando Richie termine, deber ser posible encontrar una ruta de líneas para ir de cualquier peca a otra.
La primera línea de cada caso contiene 0 < n ≤ 100, la cantidad de pecas en la espalda de Dick. Habrá una línea para describir cada peca, la cual consiste en dos números reales indicando las coordenadas (x, y) de la peca.
Tu programa debe imprimir un solo número real con dos decimales de precisión: la longitud mínima de las líneas de tinta que conectan a las pecas.
Solución: A cada punto lo consideramos como un vértice y a la distancia entre ellos como el peso de la arista. La cantidad mínima de tinta que necesitamos la podemos obtener mediante el árbol mínimo generador.
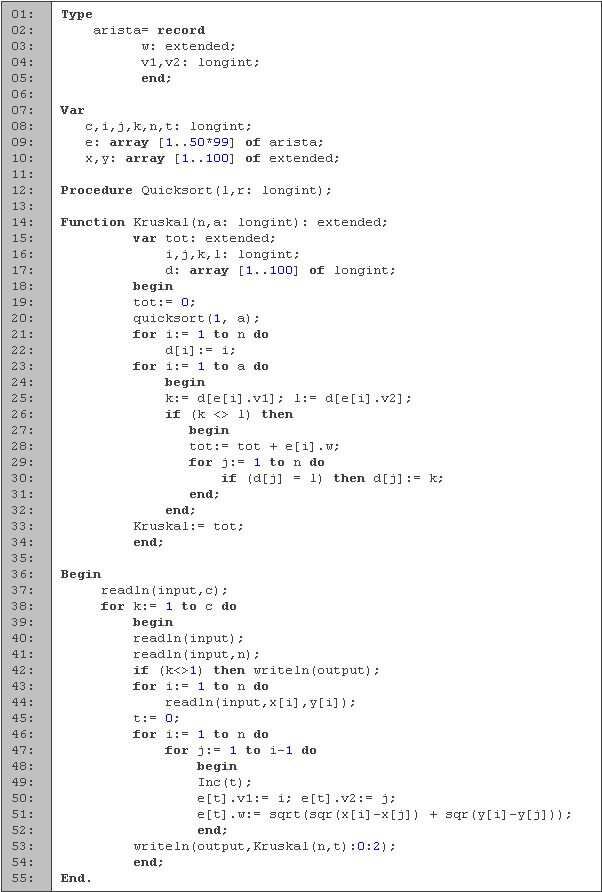
En las primeras cinco líneas definimos la estructura de las aristas, las cuales están compuestas por dos vértices (v1 y v2) y por su peso (w). En seguida tenemos la declaración de variables. Para los ciclos utilizamos los enteros i, j y k, para la cantidad de casos usamos c, para la cantidad de puntos n, y para guardar el total de aristas t. Los arreglos x e y los empleamos para la lectura de las coordenadas, y el arreglo e para guardar las aristas. Como todos los vértices están conectados entre si y la gráfica no es dirigida, la cantidad de aristas está dada por
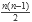y sabemos que el valor máximo de n es 100.A continuación tenemos la función con la que ordenamos las aristas (línea 12). La implementación es similar a la de la sección 3.3, pero lo modificamos ligeramente para que ordene el arreglo de aristas según sus pesos.
El árbol mínimo generador lo obtenemos en la función Kruskal de las líneas 14 a 34. Tenemos como parámetros n y a, que corresponden a la cantidad de vértices y aristas, respectivamente. Declaramos las variables i y j para los ciclos, k y l para guardar la componente a la que pertenecen los dos vértices de la arista que estamos procesando, tot para guardar el peso total del árbol, y el arreglo d para saber a que componente pertenece cada vértice.
Empezamos inicializando el total a cero (línea 19), ordenando las aristas por peso de menor a mayor (línea 20) y asignándole una componente distinta a cada vértice (líneas 21 y 22). Después procesamos cada arista (líneas 23 a 32), tomando a que componente pertenece cada vértice (línea 25) y tomando como parte del árbol mínimo si son de componentes distintos (línea 26). Una vez que sabemos que pertenecen al árbol mínimo, incrementamos el total con el valor del peso del la arista (línea 28) y juntamos los dos árboles (líneas 29 y 30). Para juntar los árboles, buscamos todos los vértices que pertenezcan a la segunda componente y les asignamos el valor de la primera. Al finalizar devolvemos el peso del árbol mínimo (línea 33). Podemos recortar un poco de tiempo contando cuantas aristas hemos utilizado y saliéndonos una vez que esto sea igual a n-1.
| Entrada: |
1 5 7.0 5.0 0.0 7.0 3.0 1.0 9.0 7.0 8.0 5.0 |
| Desarrollo: |
e[] v1 v2 w 2 1, 7.280 3 1, 5.657 3 2, 6.708 4 1, 2.828 4 2, 9.000 4 3, 8.485 5 1, 1.000 5 2, 8.246 5 3, 6.403 5 4, 2.236 v1 v2 w d[] 1, 2, 3, 4, 5 5 1, 1.000; 5, 2, 3, 4, 5 5 4, 2.236; 5, 2, 3, 5, 5 3 1, 5.657; 3, 2, 3, 3, 3 3 2, 6.708; 3, 3, 3, 3, 3 |
| Salida: | 15.60 |
El siguiente algoritmo a considerar es Prim. En este algoritmo comenzamos con cualquier vértice y lo tomamos como parte del árbol mínimo. En cada iteración, buscamos la arista de menor costo que conecte el árbol mínimo con algún vértice no utilizado. Una vez que hayamos utilizado todos los vértices, el árbol resultante es el mínimo generador. Esto se asemeja mucho a Dijkstra, ya que en ambos casos buscamos la forma de llegar a los vértices no utilizados mediante un costo mínimo.
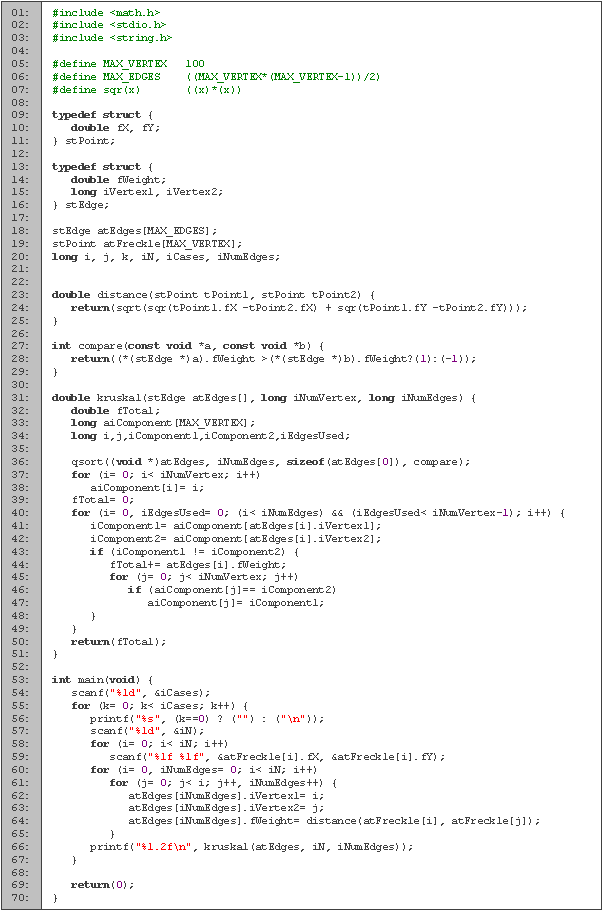
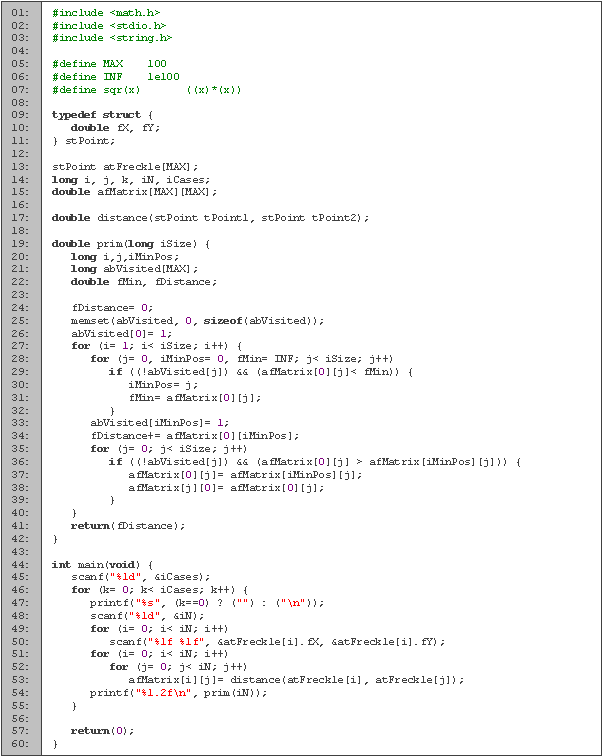
Empezamos declarando las variables (líneas 1 a 4). La mayoría de las variables están declaradas de manera análoga al código anterior, excepto m que es la matriz de adyacencia.
En seguida tenemos la función Prim (líneas 6 a 31), que es donde calculamos el árbol mínimo generador. Las variables i y j las utilizamos para los ciclos, el peso de la arista mínima la guardamos en min y su posición en p, para el peso total usamos tot y el arreglo vis lo empleamos para saber cuales vértices ya utilizamos.
Al principio inicializamos todos los no usados, excepto el primero que es desde el cual generaremos el árbol mínimo; también inicializamos el total a cero (líneas 11 y 12). A continuación utilizamos un ciclo en el cuál agregaremos un vértice en cada iteración. Empezamos buscando, entre los vértice no utilizados, la arista de menor peso que una al vértice con el árbol (líneas 15 a 20). Una vez que lo encontramos, lo marcamos como usado (línea 21) e incrementamos el peso total del árbol en el valor de la arista (línea 22). Proseguimos revisando si con el vértice que agregamos existe una arista que conecte con los vértices que no hemos utilizado y que sea de menor peso (líneas 23 a 29). Una vez obtenemos el árbol, devolvemos su peso (línea 30). Podemos observar como la implementación es prácticamente igual a la de Dijkstra, sólo que estamos guardando en el arreglo el peso de arista más liviana que nos conecta con el vértice, en lugar de la distancia más corta.
| Entrada: |
1 5 7.0 5.0 0.0 7.0 3.0 1.0 9.0 7.0 8.0 5.0 |
| Desarrollo: |
m[] 0.000 7.280 5.657 2.828 1.000 7.280 0.000 6.708 9.000 8.246 5.657 6.708 0.000 8.485 6.403 2.828 9.000 8.485 0.000 2.236 1.000 8.246 6.403 2.236 0.000 vis[]: TRUE FALSE FALSE FALSE FALSE m[1,]: 0.000 7.280 5.657 2.828 1.000 p: 5; min: 1.000, tot: 1.000 vis[]: TRUE FALSE FALSE FALSE TRUE m[1,]: 0.000 7.280 5.657 2.236 1.000 p: 4; min: 2.236, tot: 3.236 vis[]: TRUE FALSE FALSE TRUE TRUE m[1,]: 0.000 7.280 5.657 2.236 1.000 p: 3; min: 5.657, tot: 8.892 vis[]: TRUE FALSE TRUE TRUE TRUE m[1,]: 0.000 6.708 5.657 2.236 1.000 p: 2; min: 6.708, tot: 15.601 vis[]: TRUE TRUE TRUE TRUE TRUE m[1,]: 0.000 6.708 5.657 2.236 1.000 |
| Salida: | 15.60 |
Observando los ciclos para procesar cada arista y para unir los árboles (las líneas 23 y 29), notamos que la complejidad temporal de Kruskal es O(VE). Podemos mejorar este tiempo considerando unas estructuras de datos llamadas Conjuntos Disconexos (“disjoint-sets”) que se utilizan para procesar conjuntos de forma eficiente, y usando algoritmos eficaces de Unión-Búsqueda (“Union-Find”). A cada árbol lo consideramos como un conjunto y mediante la función Búsqueda determinamos si un vértice pertenece o no al árbol, y mediante Unión juntamos dos árboles en uno sólo. Al utilizar estos métodos, podemos mejorar la complejidad a O(ElgV).
Dado la similitud entre Dijkstra y Prim, podemos mejorar la complejidad de Prim tomando las mismas consideraciones que con Dijkstra.
Para escoger entre ambos algoritmos, debemos tomar en cuenta diversos factores. Uno inmediato es la forma en que está representada la gráfica, si la tenemos como una lista de adyacencia Prim es buena opción, mientras que si tenemos una lista de aristas es más conveniente usar Kruskal. Otras consideraciones incluyen la densidad de la gráfica y si la gráfica es conexa. Kruskal es buena opción para gráficas dispersas, pero para gráficas densas es mejor Prim. Para el caso del problema anterior, la gráfica es densa por lo que Prim debe correr más rápido (lo cual es cierto para las implementaciones que tenemos).
Los dos algoritmos funcionan correctamente para gráficas conexas, pero Prim no soporta gráficas no conexas. En el caso de Kruskal, al terminar de procesar todas las aristas, obtendríamos el árbol mínimo generador por cada componente de la gráfica, mientras que con Prim, de acuerdo a la implementación, podemos obtener el árbol mínimo generador de una sola componente, entrar a un ciclo infinito u obtener un resultado erróneo.
Si los vértices corresponden a puntos en el plano (como en el problema anterior), se le conoce como el árbol Euclidiano mínimo generador. Aunque puede ser resuelto como una gráfica (como acabamos de ver), existen algoritmos geométricos que pueden resolverlo de forma más eficiente.
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 01-Jun-2006 | 0.008 | 0.000 | 0.010 | 7.190 | Minimum |
| C | 25-Jun-2006 | 0.014 | Minimum | |||
| Pascal | 30-May-2006 | 0.002 | Minimum | |||
| C | 30-May-2006 | 0.004 | Minimum | |||
Valladolid:
Project Euler:
World Archive:
Camino más corto para cada pareja: Floyd-Warshall
