Below are some videos showing what I implemented for the third, fourth and fifth assignments, which were built upon the first two. Everything was coded from scratch in C/C++, so it doesn't use the GPU for anything but to put the final pixels on screen.

As class assignments, I coded in Scheme an interpreter for propositional logic (i.e. creates the truth table of a boolean formula), a rule-based system for simplifying propositional-logic formulas, a game-tree search with alfa-beta pruning for playing tic-tac-toe, and several constraint satisfaction techniques.
On the final project I worked on doing dynamic AI for a board game in flash using game-tree searches. I run somewhat out of time with the project and flash turned out to be slower than what I thought, so the search takes a lot of time and doesn't play that well. I'm hoping rework this to speed it up once I have some free time. In the meantime, a copy of my final presentation can be found here (power point) and here (pdf).

During the course we worked on how to calibrate internal and externally a camera, and how to reconstruct a 3D scene from several pictures by matching corresponding points. For the final project, I worked on a group project to reconstruct thin figures from a set of pictures without having to calibrate the camera and without user intervention. To simplify things, we decided to focus on stick figures. A friend work on the feature detection part, while I did the feature correspondence and structure reconstruction parts. A copy of our final presentation can be found here.

An independent study course I took during my third semester and that I'm continuing right now, although not for credits.
This is part of a group of ongoing projects that looks to provide educators with tools to author deaf-accessible math and science digital learning materials for grades 1-3. An important part of the project is to be able to produce expressive ASL animations without having to learn complicated animation tools (such as Maya or 3D Max).
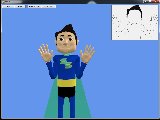
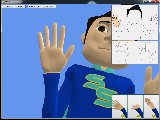
My work focused on improving the interface for posing the signing character. The program already had the functionality to modify joints, and I added the functionality to be able to modify the model's face features to create expressions by manipulating a set of 39 morph targets. I also modified the camera to automatically zoom into the selected joint or face feature, and worked on fixing several bugs and small functionality changes. This was implemented using XNA 3.1.
I'm currently working on creating and applying a user study to evaluate the design principles the GUI is based upon.
Below are some screenshots of the project (click to enlarge).

Here's an implementation of qsort using MPI that sort integers on a distributed memory system, which was the only project I did for that course (plus some written assignments).

I'm currently taking this class. For our first assignment I worked on programming an http server from scratch using C/C++. It implements a subset of HTTP 1.0 and HTTP 1.1, supports GET, HEAD, PUT, DELETE, TRACE and OPTIONS, as well as a few headers and error codes. The code can be downloaded here.

I began competing in the ICPC at the same time as my school did, so my coach (a math professor) and I didn't have a clue on what to study and where to find it. After training and competing for about three years, we got familiarized with the most common algorithms but there still was the issue that many things we learned were scattered on different bibliography and wasn't in Spanish. Which shouldn't be a problem for people ICPC since everything is in English, but it might be for the people Informatics Olympiad. And still, when you're learning something you don't really want to struggle with the language too.
In my final semester I decided to graduate by making a thesis which would be a collection of algorithms that are important to know, being approached from a contest point of view. It has been considered for publishing as a book by my undergrad university, which would hopefully happen soon (I just need to fix and polish a few things here and there).
Most of the material can be found on the algorithms section, and if you just curious about what's in, here's the table of contents in English for the thesis (in the page some things have been move around).

1. Introduction.
   1. Importance.
   2. Problematic.
   3. Methodology.
   4. Scope.
   5. Background.
   6. ICPC rules.
2. Complexity analysis.
   1. Introduction.
   2. Algorithm analysis.
   3. Best, worst and average cases.
   4. Complexity bounds.
   5. Algorithm efficiency.
   6. Class P (Polynomial) and NP (Nondeterministic Polynomial).
3. Sorting and searching.
   1. Introduction.
   2. Insertionsort.
   3. Hoare's Quicksort.
   4. Heapsort.
   5. Countsort.
   6. Linear search.
   7. Binary search.
4. Prime numbers.
   1. Introduction.
   2. Factors.
   3. Primality.
   4. Primes List.
   5. Sieve of Eratosthenes.
   6. Prime factorization.
5. Arithmetic miscellany.
   1. Introduction.
   2. Greatest common divisor and least common multiple.
   3. Extended Euclidean algorithm.
   4. Base conversion.
   5. Modular arithmetics exponentiation.
   6. Fibonacci numbers.
   7. Joseph's problem.
6. Big number arithmetics.
   1. Introduction.
   2. Storing.
   3. Reading and writing.
   4. Inequality.
   5. Bit operations.
   6. Addition.
   7. Subtraction.
   8. Multiplication.
   9. Division and modulo (remainder).
   10. Square root.
7. Geometric algorithms.
   1. Introduction.
   2. Maximum number of points lying on a line.
   3. Intersection line with line, line with segment, and segment with segment.
   4. Triangle incircle and circumcircle.
   5. Area of a polygon.
   6. Convex hull.
   7. Centroid.
8. Dynamic programming.
   1. Introduction.
   2. Maximum interval sum.
   3. Longest Increasing / Decreasing Subsequence (LIS, LDS).
   4. Longest Common Subsequence (LCS).
   5. Edit distance.
   6. Zero-One Knapsack.
   7. Counting change.
   8. Integer partition.
   9. Matrix chain multiplication.
9. Exhaustive searching and backtracking.
   1. Introduction.
   2. Farey sequence and Stern-Brocot tree.
   3. Floodfill.
   4. Shortest distance in a maze.
   5. Permutations.
   6. Prunes.
   7. Eight queens problem.
   8. Sudoku.
10. Graphs.
    1. Introduction.
    2. Bicoloring.
    3. Topological sort.
    4. Shortest path: Dijkstra.
    5. All pairs shortest path: Floyd-Warshall.
    6. Minimum Spanning Trees: Prim and Kruskal.
    7. Eulerian Path.
    8. Articulation point (cut vertex).
11. Other.
    1. Introduction.
    2. Root-finding algorithms.
    3. Solutions of a system of linear equations.
    4. Basic data structures (stacks, queues and linked lists).
    5. Binary trees.
    6. Greedy algorithms.
    7. Divide and conquer.
12. Codes in C.
    1. Sorting and searching.
    2. Prime numbers.
    3. Arithmetic miscellany.
    4. Big number arithmetics.
    5. Geometric algorithms.
    6. Dynamic programming.
    7. Exhaustive searching and backtracking.
    8. Graphs.
    9. Other.
       

Appendix:

1. Contest strategies.
2. Pascal reference.
3. C reference.
4. Divisors y congruence properties.
5. Internet links.
6. Run-time errors table.
7. Symbols.
8. Groups of problems by category.
9. Internal contest problems.
10. Regional contest problems.
11. Performance statistics of Pacal and C codes.
12. ASCII table.