El algoritmo de Euclides no sólo sirve para encontrar el máximo común divisor de dos números, sino que también nos indica que el mcd se puede expresar como combinación lineal de los mismos. Además, el mcd es el menor entero positivo en que estos dos números se pueden usar como combinación lineal. Lo que buscamos con el algoritmo extendido de Euclides, son los coeficientes de esta combinación lineal.

Esta propiedad resulta de gran utilidad, sobre todo al momento de resolver ecuaciones Diofantinas (ecuaciones de la forma ax + by = c, donde todos son enteros y a, b y c son constantes).

Otra aplicación útil es que cuando a y b son primos relativos (por lo que c = 1), entonces x es el inverso multiplicativo de a módulo b. Por ejemplo, para 5x + 3y = 1, una solución es 5(-1) + 3(2) = 1, y tenemos que 5(-1) ≡ 1 mod 3 y 3(2) ≡ 1 mod 5.

Para encontrar los valores de x e y, consideremos lo siguiente. Expresando el mcd como combinación lineal de las entradas, implica que c = mcd:
mcd(a,b) = ax + by
También sabemos que:
mcd(a,b) = mcd(b, a mod b)
Si hacemos que a₁ = a, b₁ = b, a₂ = b y b₂ = (a mod b) = a -bk, donde k es entero, entonces:
mcd(a₁, b₁) = mcd(a₂, b₂)
Reemplazando en la primera ecuación tenemos:
mcd(a₁, b₁) = a₁x₁ + b₁y₁
mcd(a₂, b₂) = a₂x₂ + b₂y₂
…
mcd(a_n, b_n) = a_nx_n + b_ny_n
Si hacemos mcd(a,b) = d, y suponiendo que tenemos dos iteraciones además de los valores de x e y para la segunda (x₂, y₂):
mcd(a₁, b₁) = a₁x₁ + b₁y₁ = d
mcd(a₂, b₂) = a₂x₂ + b₂y₂ = d

Sabemos que a₂ = b₁, b₂ = a₁ -b₁k y k = 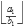, por lo que:
d = a₁x₁ + b₁y₁
d = a₂x₂ + b₂y₂ = b₁x₂ + (a₁ -b₁k)y₂

Uniendo las dos ecuaciones:
a₁x₁ + b₁y₁ = b₁x₂ + (a₁ -b₁k)y₂
= a₁y₂ + b₁(x₂ -ky₂)
Lo anterior se cumple si:
x₁ = y₂
y y₁ = x₂ -ky₂ = x₂ - 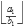y₂
Con esto, podemos calcular los valores de x e y en base a lo anteriores. Ahora sólo necesitamos obtener cuales son los valores iniciales.

Sabemos que en la última iteración a_n = d y b_n = 0, entonces nos queda que:
mcd(a_n, b_n) = a_nx_n + b_ny_n
d = dx_n + 0y_n
x_n = 1, y_n = 0



Solución: Aplicando el algoritmo extendido de Euclides podemos encontrar una solución. Tomando a los valores que arroja el algoritmo de Euclides como x₀ e y₀, y a t como una variable entera, las demás soluciones las podemos calcular a partir de la anterior, utilizando la siguiente fórmula:
d = a(x₀ + 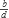t) + b(y₀ - 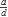t)
Por lo que los valores de x e y son de la forma:
x = x₀ + 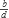t
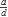y = y₀ - t
Además sí sabemos que la gráfica de la ecuación f(t) = |x = x₀ + 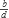t| + |y = y₀ - 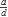t| está compuesta por tres rectas, las cuales forman algo semejante a una V. Por lo que en caso de que existan valores enteros más pequeños que f(0), los podemos obtener ya sea incrementando o decrementado t.




En las primeras dos líneas declaramos las variables que vamos a utilizar: leemos la entrada en a y b, y guardamos el resultado en x, y y d, con lo que utilizamos la misma notación que la que maneja el problema.

Entre las líneas 4 y 15 tenemos la versión extendida del algoritmo de Euclides. Para poder hacer que la función devuelva tres valores, hacemos un procedimiento en el que tres de los parámetros puedan ser modificadas (esto es, pasamos las variables por referencia, en lugar de por valor; en Pascal escribimos var antes de declararlas). Las líneas 8 y 11 son similares a las del algoritmo convencional, sólo que añadimos los valores iniciales de x y y en la línea 8, y en la línea 11 incluimos x, y y d como parámetros. En las líneas 12 y 13 calculamos los nuevos valores de x y y, respaldando primero los valores en x1 y y1. Es importante notar que los valores de x y y los calculamos después de mandar llamar la función.

La parte principal del programa lo encontramos entre las líneas 17 y 34. Lo que hacemos en esta parte del código es leer a y b, mandar llamar el algoritmo extendido de Euclides, buscar hacia los dos lados de la gráfica por soluciones más pequeñas e imprimir los resultados, todo esto mientras no lleguemos al fin de archivo.

Entrada:	25 58
Desarrollo:	mcd(25,58) = mcd(58, 25 mod 58) mcd(58,25) = mcd(25, 58 mod 25) mcd(25, 8) = mcd( 8, 25 mod  8) mcd( 8, 1) = mcd( 1,  8 mod  1) mcd( 1, 0) = 1        x=  1, y=  0  8  1; x=  0, y=  1 –( 8/ 1)×0 = 1, d= 1 25  8; x=  1, y=  0 –(25/ 8)×1 =-3, d= 1 58 25; x= -3, y=  1 –(58/25)×-3= 7, d= 1 25 58; x=  7, y= -3 –(25/58)×7 =-3, d= 1
Salida:	7 –3 1

Entrada:	4 6
Desarrollo:	mcd( 4, 6)= mcd( 6, 4 mod 6) mcd( 6, 4)= mcd( 4, 6 mod 4) mcd( 4, 2)= mcd( 2, 4 mod 2) mcd( 2, 0)= 2      x=  1, y=  0 2 4; x=  0, y=  1 -(2/4)×0 = 1, d= 1 2 4; x=  1, y=  0 -(6/4)×1 =-1, d= 1 4 6; x= -1, y=  1 –(4/6)×-1= 1, d= 1
Salida:	-1 1 2

Entrada:	17 17
Desarrollo:	mcd(17,17) = mcd(17, 17 mod 17) mcd(17, 0) = 17        x=  1, y=  0 17 17; x=  0, y=  1 –(17/17)×0 = 1, d= 1
Salida:	0 1 17

Nota: En las operaciones de división, sólo se toma la parte entera (y esto aplica para el resto del capítulo).

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	13-Ene-2006	1.529	0.316	1.041	9.871	324
C	17-Feb-2006	0.734				388