En un sistema posicional de base b se suelen utilizar b dígitos para representar los números. Comúnmente los dígitos empleados son 0, 1, …, |b|-1, y para dígitos mayores a 9, generalmente se emplean letras mayúsculas, por ejemplo A= 10, B= 11, etc. Según la base que escojamos, tendremos una representación conocida como sistema de numeración.

Se les denomina sistemas posicionales ya que el primer dígito a la izquierda del punto decimal (las unidades) conserva su propio valor, mientras que cada que nos movemos un lugar a la izquierda, el valor del dígito se multiplica por b (esto es, cambia según su posición). Las bases más comúnmente utilizadas son la 10 (decimal) que es la que normalmente empleamos, la 2 (binaria) y la 16 (hexadecimal) que son ampliamente usadas en la computación.

Al escribir un número entero, anotamos todos los dígitos de forma sucesiva n = a_ka_k-1…a₀, aunque en realidad lo que estamos expresando es n = a_kb^k + a_k-1b^k-1 + … + a₀b⁰. Cabe señalar que b⁰ = 1. Por ejemplo, si tenemos el número 1982 en base 10, lo que estamos representando es 1×10³ + 9×10² + 8×10 + 2.

Cuando se utilizan varias bases al representar números, se acostumbra anotar como subíndice al final del número la base, por ejemplo: 25₁₀ = 31₈ (25 base diez es igual a 31 base ocho). Si no se especifica la base, se sobreentiende que se trata de base diez. Algunas veces se utilizan prefijos para identificar bases, por ejemplo en Pascal se utiliza el signo de pesos (‘$’) y en C un cero y una x (‘0x’) para denotar los números hexadecimales.

Para un número fraccionario, lo que hacemos es separar la parte fraccionaria de la entera mediante un punto y escribir la parte fraccionaria mediante potencias negativas de la base. Por ejemplo, 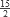= 7.5 = 7×10⁰ + 5×10^-1.

Comúnmente se utilizan como base algún número natural, aunque también es posible recurrir a números negativos (como las bases negadecimal y negabinario), números irracionales (como π), e inclusive bases complejas (como 1+i). En bases no naturales se puede dar el caso de que un número tenga más de una representación.

Para convertir de una base (b₁) a otra (b₂), podemos utilizar alguno de los siguientes algoritmos:

Teniendo que n = a_kb₁^k + a_k-1b₁^k-1 + … + a₀b₁⁰, convertimos el valor de b₁ y todas las a_i (0 ≤ i ≤ k) a su equivalente en b₂ y realizamos las operaciones de suma y multiplicación en esta base. Por ejemplo, si queremos pasar 217 de base 8 a base 5, tenemos que:

El inconveniente obvio que presenta este método es que necesitamos tener la conversión de todos los dígitos de la base b₁ a la base b₂ para poder convertir el número completo. Por esto, este método es útil principalmente cuando b₁ < b₂.

Otra forma para convertir entre bases es ir dividir el número en base b₁ entre b₂, tomar el cociente y repetir hasta que el cociente sea cero. Al final, el número en base b₂ se conforma por los residuos, leyéndolos del último al primero. Utilizando los mismos números y bases del ejemplo anterior, tenemos que (las operaciones son en base 8):

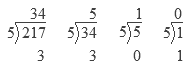
Si queremos convertir entre bases, y una de estas es potencias de la otra, existe una forma para hacer más rápida la conversión. Teniendo que b₂ = b₁ⁱ, entonces podemos separar al número en base b₁ en bloques de tamaño i, convertir esos bloques y después unirlos.

Por ejemplo, si queremos cambiar 7BE de base 16 a base 2, sabemos que 7₁₆ = 0111₂, B₁₆ = 1011₂ y E₁₆ = 1110, por lo que 7BE₁₆ = 011110111110₂ (podemos omitir el primer cero). Si ahora lo queremos pasar a base 8, lo separamos en bloques de 3: 011110111110₂ → 011₂110₂111₂110₂, como 011₂ = 3, 110₂ = 6 y 111₂ = 7, entonces 011110111110₂ = 3676₈.

Para convertir un número con decimales a otra base, podemos utilizar el siguiente algoritmo. Para la parte entera, utilizamos cualquiera de los métodos anteriores y para la parte decimal realizamos lo siguiente: multiplicamos los decimales de b₁ por b₂, la parte entera del resultado la tomamos como el primer dígito de la conversión y con la parte decimal repetimos el procedimiento. Por ejemplo, para pasar 0.2205 de base 6 a base 2 (las operaciones son en base 6):

Nota: un número que tiene una cantidad finita de decimales en una base puede tener una cantidad infinita en otra.




Solución: Para cambiar de una base a otra, vamos a utilizar como paso intermedio la base 10. Esto se debe a que si quisiéramos omitir la conversión intermedia, necesitaríamos tener implementaciones de las operaciones básicas (+, -, ×, ÷) en todas las bases.




En las primeras tres líneas declaramos las variables que vamos a utilizar: s es la cadena en la que guardamos el número original, i es para los ciclos, b1 y b2 son la base original y la base a convertir, respectivamente. El tamaño de s es de 7 para leer únicamente los primeros 7 caracteres.

En la siguiente función (líneas 5 a 16) cambiamos de la base original a base 10. Como parámetros tenemos el número original n en forma de cadena y la base original b. La variable i la utilizamos para los ciclos, t como variable temporal y r para guardar el resultado. Empezamos inicializando el resultado a cero (línea 8), y revisamos dígito por dígito el número original (línea 9 a 14). Entre las líneas 11 y 12 pasamos el dígito de caracter a número: si el dígito está entre 0 y 9, entonces restamos 48 (ASCII del cero), en caso contrario, restamos 55 (ASCII de la A mayúscula menos diez). Después multiplicamos el resultado temporal por la base (equivale a incrementar en uno todas las potencias) y le agregamos el nuevo número. Terminamos regresando el resultado (línea 15).

En seguida tenemos la función que cambia un número de base 10 a otra base (líneas 18 a 33). Utilizamos el mismo nombre de variables para el mismo uso, sólo que cambiamos algunas cadenas a enteros y viceversa. Empezamos inicializando el resultado (líneas 22 y 23), tomando en cuenta el caso especial en que n es cero. Para cambiar el número de base, utilizamos el método de dividir entre la nueva base hasta llegar a cero (líneas 24 a 30). Esto lo hacemos dividiendo el número entre la base y agregando cada residuo al final de r (teniendo en cuenta que el resultado es una cadena). Acabamos revisando si el resultado cabe en la pantalla (esta línea se debe omitir en otros programas) y regresándolo.

La parte principal del código la tenemos entre las líneas 35 a 42, en la cual repetimos el proceso mientras no lleguemos al fin de archivo. En la línea 38 leemos el número, la base en la que está y la base a la que lo cambiaremos. Después de leer el número, parchamos los espacios con ceros (líneas 39 y 40). En lenguajes como C esto no es necesario, ya que se pueden leer las cadenas sin incluir los espacios. Por últimos escribimos el resultado del cambio de bases (línea 41).

Entrada:	2102101  3 10
Desarrollo:	2102101       r= 0 t= 2, r= 3*0 + 2= 2 t= 1, r= 3*2 + 1= 7 t= 0, r= 3*7 + 0= 21 t= 2, r= 3*21 + 2= 65 t= 1, r= 3*65 + 1= 196 t= 0, r= 3*196 + 0= 588 t= 1, r= 3*588 + 1= 1765                    r= '' t= 1765 mod 10= 5, r= '5' t=  176 mod 10= 6, r= '65' t=   17 mod 10= 7, r= '765' t=    1 mod 10= 1, r= '1765' length('1765')= 4 ≤ 7
Salida:	1765

Entrada:	12312  4  2
Desarrollo:	12312       r= 0 t= 1, r= 4*0 + 1 = 1 t= 2, r= 4*1 + 2 = 6 t= 3, r= 4*6 + 3 = 27 t= 1, r= 4*27 + 1 = 109 t= 2, r= 4*109 + 2 = 438                  r= '' t= 438 mod 2= 0, r= '0' t= 219 mod 2= 1, r= '10' t= 109 mod 2= 1, r= '110' t=  54 mod 2= 0, r= '0110' t=  27 mod 2= 1, r= '10110' t=  13 mod 2= 1, r= '110110' t=   6 mod 2= 0, r= '0110110' t=   3 mod 2= 1, r= '10110110' t=   1 mod 2= 1, r= '110110110' length('10010110110')= 9 > 7
Salida:	ERROR

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	09-Mar-2006	1.807	0.070	0.746	20.040	324
C	04-May-2006	0.404				388

Valladollid:

Ural:

Project Euler:

Zhejiang: