Una operación frecuente en teoría de números es obtener el módulo de un número elevado a cierta potencia. Esto es, dado los números x, n y m, encontrar una y tal que y ≡ xⁿ mod m. Esta operación es esencial ya que se utiliza en varias pruebas de primalidad y en algoritmos de encriptación.

Para realizar esta operación, lo primero que podemos hacer es multiplicar n veces x y después obtener el módulo. El problema de este enfoque es que al realizar las multiplicaciones, el resultado crece rápidamente. La forma de solucionarlo es obteniendo el módulo después de cada multiplicación, con lo que logramos mantener los cálculos en un rango aceptable.

Es claro que la complejidad de este algoritmo es Θ(n). Podemos obtener un algoritmo que tenga mejor complejidad basándonos en lo siguiente:

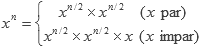
Esta fórmula la podemos aplicar de forma recursiva hasta obtener la solución. De esta manera, tenemos un algoritmo Θ(lgn).




Solución: Recorremos todo el intervalo en busca de las y que cumplan, y cada que encontremos una respuesta la imprimimos. Contamos cuantas respuestas obtuvimos, y en caso de que sean cero, imprimimos –1 como resultado.



En las primeras dos líneas declaramos las variables a utilizar. En c contamos cuantas soluciones hemos encontrado, mientras que las demás variables son las mismas descritas en el problema.

Enseguida tenemos las función bigmod (líneas 4 a 14) que es la que encuentra el módulo de la potencia. Las líneas 7 y 8 son los casos base con los que termina la recursividad. En caso de que la potencia sea par, la separamos en mitades, encontramos la solución de la mitad (línea 10) y con esto calculamos el resultado (línea 11). En caso de que sea impar, le restamos uno a la potencia, con lo que podemos utilizar el caso de la par, y lo multiplicamos por la base.

Entre las líneas 16 y 26 tenemos la parte principal del programa. Empezamos declarando la cantidad de soluciones a cero (línea 17) y leemos la entrada (línea 18). Hacemos un barrido con todas las posibles soluciones y en caso de que alguna cumpla, la imprimimos e incrementamos el total de soluciones (líneas 20 a 24). En caso de que no encontremos solución alguna, imprimimos “–1”. Aunque el problema indica que x puede ser cero, nos saltamos este caso ya que y no puede serlo.

Entrada:	13 4 3
Desarrollo:	x= 1 n= 13, r= (1×1)×1 = 1 n= 12, r= 1×1 = 1 n=  6, r= 1×1 = 1 n=  3, r= (1×1)×1 = 1 n=  2, r= 1×1 = 1 n=  1, r= 1 1 ≠ 3 x= 2 n= 13, r= (0×0)×2 = 0 n= 12, r= (0×0) = 0 n=  6, r= (0×0) = 0 n=  3, r= (0×0)×2 = 0 n=  2, r= (2×2) = 4 ≡ 0 (mod 4) n=  1, r= 2 0 ≠ 3 x= 3 n= 13, r= (1×1)×3 = 3 n= 12, r= (1×1) = 1 n=  6, r= (3×3) = 9 ≡ 1 (mod 4) n=  3, r= (1×1)×3 = 3 n=  2, r= (3×3) = 9 ≡ 1 (mod 4) n=  1, r= 3 3 = 3
Salida:	3

La desventaja más clara de este algoritmo es la recursividad, ya que ocupa más espacio en memoria y alenta la ejecución. Este no es mucho problema con números pequeños, pero si queremos utilizar números grandes (como en la sección 6.8) o matrices (como en la siguiente sección), es conveniente hacerlo iterativo.

Para hacer esto, vamos a descomponer el exponente en potencias de dos. Teniendo que n = b_k + b_k-1 + … + b₀, entonces xⁿ = x^b_k×x^b_k-1×…×x^b₀. La primera potencia de x ya la tenemos al comenzar (x¹), mientras que las subsecuentes las calculamos elevando la anterior al cuadrado. Entonces, empezamos con x, en cada paso lo elevamos al cuadrado y vemos si lo utilizamos o no. Por ejemplo: x⁴⁵ = x³²×x⁸×x⁴×x¹ (las potencias x² y x¹⁶ si las calculamos, pero no las utilizamos).


Empezamos inicializando el resultado r a uno en la línea 4. En la línea 8 es donde vamos elevando al cuadrado para obtener la siguiente potencia de dos. El exponente n lo dividimos entre 2 en cada ciclo (línea 10) con lo que estamos recorriendo los dígitos un lugar a la derecha en base 2, y podemos saber si multiplicar o no con saber si el número es impar (líneas 7 y 8). El ciclo termina cuando n se hace cero (línea 5). Finalizamos devolviendo el resultado (línea 12).

Entrada:	13 4 3
Desarrollo:	n= 13, x= 1, r= 1×1 = 1 n=  6, x= 1, r= 1 n=  3, x= 1, r= 1×1 = 1 n=  1, x= 1, r= 1×1 = 1 1 ≠ 3 x= 2 n= 13, x= 2, r= 1×1 = 1 n=  6, x= 0, r= 1 n=  3, x= 0, r= 1×0 = 0 n=  1, x= 0, r= 0×0 = 0 0 ≠ 3 x= 3 n= 13, x= 3, r= (1×1) = 1 n=  6, x= 1, r= 1 n=  3, x= 3, r= (1×3) = 3 n=  1, x= 1, r= (3×1) = 3 3 = 3
Salida:	3

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	18-Feb-2006	0.001	0.001	0.040	0.359	122
C	17-Feb-2006	0.001				122
Pascal	18-Feb-2006	0.015				122
C	18-Feb-2006	0.015				130

Valladollid:

Saratov: