En el siglo XIII, el matemático Leonardo de Pisa (mejor conocido como Fibonacci) estudió la forma en que crecía una población de conejos. Para saber cuantas parejas de conejos había en determinado momento, generalizó su crecimiento de forma ideal considerando que en el primer mes sólo existe una pareja, cada pareja puede reproducirse a partir del segundo mes, cada mes todas las parejas fértiles daban luz a una nueva pareja y los conejos nunca mueren. Utilizando estas reglas, la cantidad de parejas a través de los meses son: 1, 1, 2, 3, 5, 8, ..., y en general, para un mes n la cantidad de parejas Fn es igual a Fn-1 + Fn-2.
A pesar de que estos números son conocidos como números de Fibonacci, se cree que tribus Hindúes utilizaban esta sucesión desde algunos años antes para estudiar la cantidad de melodías que se pueden formar utilizando notas de uno o dos golpes.
Los números de Fibonacci aparecen con frecuencia en la naturaleza, principalmente en la botánica, donde a su presencia se le conoce como la ley de Ludwig. Por ejemplo, en las margaritas se encuentran 21 espirales en sentido de las manecillas del reloj y 34 en contra; otras relaciones que se han encontrado son 1-2 (olmo), 1-3 (avellana), 2-5 (roble), 3-8 (rosa), 5-13 (almendra), 8-13 (piña), etc.
Los números de Fibonacci también se pueden encontrar en otros lugares diversos como en la cantidad de ancestros que tiene una abeja macho, en las diagonales del triángulo de Pascal, en la música (principalmente para entonar), y en la pintura (principalmente por su relación con el rectángulo dorado).
Otras curiosidades que presentan estos números incluyen que el cociente de dos números de Fibonacci
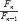 tiende a φ (número áureo) cuando n tiende a infinito. Cualquier número natural puede ser escrito de forma única como la suma de números de Fibonacci, sin que se incluyan dos consecutivos (teorema de Zeckendorf’s). Además de esto, los números de Fibonacci son utilizados en generadores de números pseudo-aleatorios.
tiende a φ (número áureo) cuando n tiende a infinito. Cualquier número natural puede ser escrito de forma única como la suma de números de Fibonacci, sin que se incluyan dos consecutivos (teorema de Zeckendorf’s). Además de esto, los números de Fibonacci son utilizados en generadores de números pseudo-aleatorios.Los números de Fibonacci se calculan mediante la siguiente fórmula:
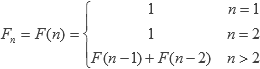
La fórmula se puede implementar recursivamente sin muchos problemas. El inconveniente de este método es que corre en tiempo exponencial (Θ(Fn) = Θ(φn)) ya que repetimos muchos cálculos, pero lo podemos bajar a tiempo lineal “recordando” los resultados que hayamos calculado con anterioridad.
Problema ejemplo
La suma
Problema
La serie de Fibonacci se define como: F1 = 1; F2 = 1; Fn+1 = Fn + Fn-1, para toda n > 1. Tienes que encontrar s – la suma de los primeros k números de Fibonacci.Entrada
La primera línea tiene un número natural k (0 < k < 41).Salida
La primera línea debe tener el número s.Solución: Queremos encontrar sk = Fk + Fk-1 + … + F2 + F1. Si lo sumamos consigo mismo obtenemos:
sk + sk = Fk + Fk + Fk-1 + Fk-1 + … + F2 + F2 + F1 + F1
2sk = Fk + (Fk + Fk-1) + (Fk-1 + Fk-2) + … + (F2 + F1) + F1
2sk = Fk + (Fk+1 + … + F3) + F1
2sk = (Fk + Fk+1) + (Fk + … + F3 + F2 + F1) - F2
2sk = Fk+2 + sk - F2
sk = Fk+2 - F2
sk = Fk+2 - 1
Nota: En problemas en el que la entrada no toma muchos valores (40 en este caso), una buena estrategia durante un concurso es precalcular todos los posibles resultados, aunque en este caso no será necesario.
Código

En las primeras dos líneas declaramos el único entero que vamos a utilizar, k, el cual usaremos para leer la entrada.
La siguiente función (líneas 4 a 13) calcula el número de Fibonacci para una entrada n. En la línea 11 utilizamos la fórmula para obtener el siguiente fibonacci, y utilizamos el arreglo fib para no tener que volver a calcular los datos anteriores. Las líneas 8 y 9 sirven para obtener los primeros dos valores. En la línea 12 devolvemos el resultado. Si necesitáramos utilizar más de un valor en el problema, podemos declarar fib como global y obtener los datos a través del arreglo en lugar de la función.
Caso ejemplo
| Entrada: | 5 |
| Desarrollo: |
1 1 1 1 2 1 1 2 3 1 1 2 3 5 1 1 2 3 5 8 1 1 2 3 5 8 13 13 –1 = 12 |
| Salida: | 12 |
Posibles Cambios
Algo que podemos observar es que sólo necesitamos los últimos dos valores para calcular el siguiente, lo cual podemos aprovechar. Si tenemos que a= 1 y b= 1, el siguiente número lo podemos obtener sumándole b a a, con lo que tendríamos a= 2 y b= 1; después sumamos a a b, con lo que obtenemos a= 2 y b= 3. Podemos ir repitiendo el mismo procedimiento indefinidamente, con lo que en cada iteración el valor de Fn se intercambiando entre a y b. Por ejemplo, para calcular F10:
| Fn | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| a | 1 | 2 | 2 | 5 | 5 | 13 | 13 | 34 | 34 | 89 |
| b | 1 | 1 | 3 | 3 | 8 | 8 | 21 | 21 | 55 | 55 |
El algoritmo utiliza n sumas, por lo que su complejidad es de Θ(n), al igual que el anterior. El único cambio es que ya no utilizamos el arreglo, lo cual es una ventaja si necesitamos calcular uno o pocos Fn.

En la función tenemos definidas a y b para utilizarlas como vimos anteriormente, e i para utilizarla como variable de ciclo (línea 2). Inicializamos los valores (línea 4), y los vamos calculando intercaladamente (líneas 5 a 7). Al final devolvemos el valor que corresponda (líneas 8 y 9).
Otro enfoque: Matrices
Otra forma en que podemos calcular los números de Fibonacci es mediante el uso de matrices. Tenemos que:
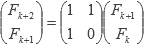
Agregando otra columna obtenemos:
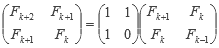
Si vamos reemplazando la matriz de la derecha utilizando la misma fórmula, obtendríamos:
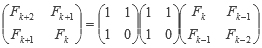
Repitiendo el proceso k-1 veces:
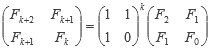
Sabiendo que F2 = F1 = 1 y F0 = 0:
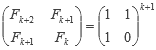
Podemos utilizar el mismo algoritmo del tema anterior para elevar potencias, con lo que obtendríamos Fn en Θ(lgn).

En las líneas 1 y 2 definimos el tipo de variable matriz_dos que es la que utilizaremos para las operaciones de matrices. La función multiplica (líneas 4 a 12) la utilizamos para multiplicar dos matrices cuadradas (multiplicamos renglón por columna, según corresponda para cada casilla). La función Fibonacci (líneas 14 a 27) es prácticamente igual la segunda función bigmod de la sección anterior, con el cambio de que aquí utilizamos matrices en lugar de enteros.
Otro enfoque: Fórmula
Por último, también podemos calcular Fn utilizando una fórmula directa. Una ecuación se dice que es de recurrencia lineal (u homogénea) si es de la forma:
f(n) = a1f(n-1) + a2f(n-2) + … + akf(n-k)
Para resolverla, hacemos un cambio f(n) = xn, con lo que obtenemos la ecuación característica asociada:
xn = a1xn-1 + a2xn-2 + … + akxn-k
Estas ecuaciones tienen solución en la siguiente expresión, siempre y cuando todas las raíces sean distintas:
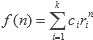
Donde ri es la i-ésima raíz, y ci es una constante que se determina a partir de las condiciones iniciales.
En el caso de la ecuación de Fibonacci, tenemos que k = 2 y a1 = a2 = 1, por lo que la ecuación queda de la siguiente forma:
x2 = x -1
Las raíces de esta ecuación son:
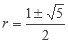
La solución de la ecuación es:
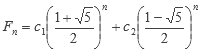
Utilizando F0 = 0 y F1 = 1 y obtenemos:
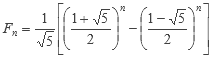

A diferencia de otros lenguajes, Pascal no cuenta con funciones de exponencial, excepto para potencias de e, por lo que debemos hacerlas nosotros. Para esto, vamos a aprovechar que sí cuenta con funciones de logaritmos:
y = xn
y = elnxn
y = en×lnx
Un problema de utilizar este cambio, es que si x es negativo, lnx no está definido en los reales (por lo que causaría error de ejecución). Para poder solucionar esto, tomamos a x con su valor absoluto y ajustamos el signo según se requiera (negativo si n es impar, y positivo si no lo es).
Otro inconveniente con esta fórmula es que utiliza números flotantes y las operaciones intermedias toman valores grandes, por lo que pierde precisión rápidamente cuando n crece, debido a errores de redondeo.
Códigos en C



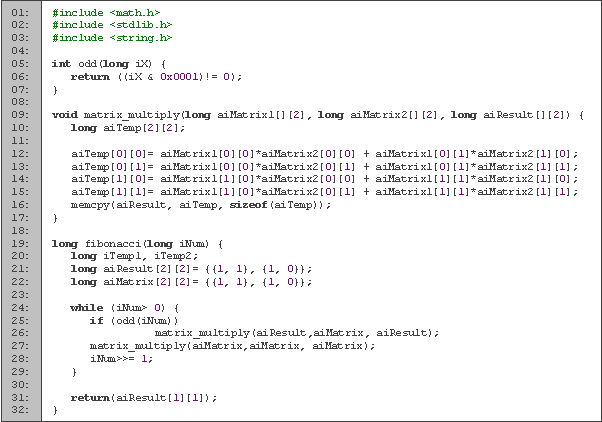
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 16-Mar-2006 | 0.040 | 0.000 | - | - | 125 |
| C | 16-Mar-2006 | 0.060 | 358 | |||
| Pascal | 18-Feb-2006 | 0.045 | 129 | |||
| C | 17-Feb-2006 | 0.067 | 366 | |||
| Pascal | 19-Feb-2006 | 0.045 | 129 | |||
| C | 17-Feb-2006 | 0.067 | 402 | |||
| Pascal | 18-Feb-2006 | 0.044 | 129 | |||
| C | 17-Feb-2006 | 0.066 | 358 | |||
Otros problemas
Valladollid:
Ural:
Project Euler:
Zhejiang:
El Judge:
 Exponenciales con módulo
Exponenciales con módulo
