También conocido como el problema de Josephus, lo que en español sería José, toma su nombre de un historiador judío del siglo primero llamado Flavius Josephus. Lo que busca el problema de Joseph es la única persona que sobreviviría de entre un grupo de n personas si cada m son ejecutados. Existen variantes como encontrar cuales personas quedan vivas después de k muertes, o encontrar el orden en que fueron eliminadas las personas.

La leyenda relata que durante una guerra contra los romanos, Joseph y 40 soldados fueron rodeados por el ejército romano. El grupo decidió morir antes que rendirse ante el enemigo, pero Joseph y otro colega no estaban de acuerdo con esta idea. El método que escogieron para suicidarse fue el formarse en un círculo e irse matando cada tercer persona. Joseph y su amigo escogieron las posiciones con las que serían los últimos. Cuando sólo quedaban ellos dos, fueron y se rindieron ante los romanos.

Para programarlo, la primera idea que se nos puede ocurrir es crear un arreglo de boléanos con una casilla por cada persona que indique si la persona ya fue ejecutada. Inicializamos todas las casillas a false, y cada que eliminemos a alguien, a su casilla le asignamos true. Al momento de estar contando, nos saltamos todas las casillas que ya estén eliminadas. Repetimos hasta que sólo quede uno.

Un problema es que cuando quedan pocos vivos, estar recorriendo el arreglo se vuelve tardado. Para solucionar esto, a cada persona le agregamos cual es el que le sigue. Entonces, al eliminar a alguien, no sólo le asignamos true sino que también le decimos al anterior que se lo salte. Las listas en las que sabemos cual elemento es el que sigue o el que le antecede se conocen como listas enlazadas y se comentan brevemente en la sección 11.4.

Otra mejora para esto, es que si vamos a contar más veces de las personas que quedan, podemos reducir el conteo mediante residuos. Por ejemplo, si quedan 3 personas y vamos a eliminar cada 8, es lo mismo que si eliminamos cada 2.




Solución: Lo que estamos buscando es equivalente al problema de Joseph, sólo que con caracteres en lugar de personas. La cantidad de caracteres varía de acuerdo a la entrada, pero siempre eliminamos cada 1999 caracteres. Una vez que calculemos el último caracter, revisamos cuál es y damos una respuesta acorde.




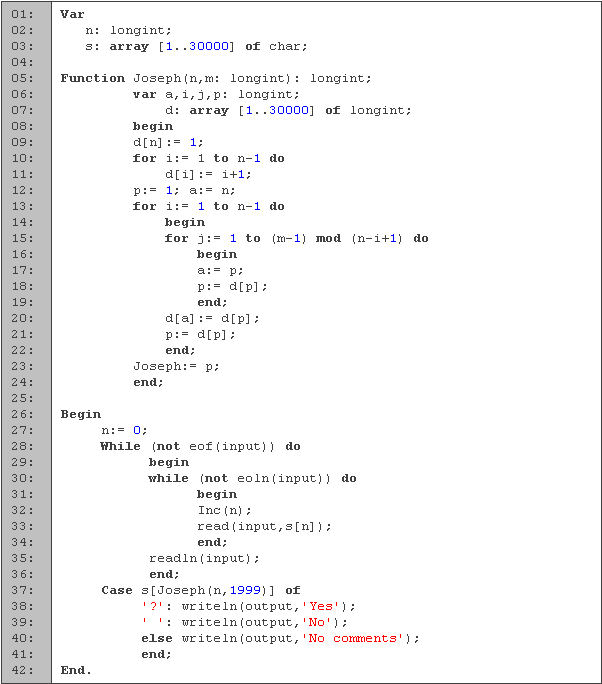
En las primeras tres líneas declaramos las constantes a utilizar. En n guardamos la cantidad de caracteres, mientras que en s guardamos la pregunta.

En la función joseph (líneas 5 a 24) calculamos la posición de la última casilla. Las variables i y j las utilizamos para los ciclos, p es nuestra posición actual, a la anterior y d es el arreglo que nos indica cual es el siguiente. En esta ocasión no necesitamos utilizar booleanos para saber si están eliminados, ya que sólo necesitamos saber la posición del último.

Entre las líneas 9 y 11 inicializamos a d para que nos de la posición del siguiente caracter. Después inicializamos t al primer caracter y a a al último. En cada iteración del ciclo de la línea 13 eliminamos un caracter. Normalmente el siguiente ciclo (línea 15) sería hasta m-1 (1998) pero aprovechamos que la cantidad de datos que sobran en la iteración i son n-i + 1. Dentro del ciclo, lo único que hacemos es actualizar el valor anterior al actual y el actual al siguiente (líneas 17 y 18). Al terminar el ciclo, quitamos el actual haciendo que el que lo apuntaba como siguiente se lo salte (líneas 20 y 21).

La parte principal del código la encontramos entre las líneas 26 y 42. Empezamos inicializando a cero la cantidad de caracteres (línea 27). Entre las líneas 28 y 36 leemos caracter por caracter toda la cadena, saltándonos los fines de línea, hasta que lleguemos al fin de archivo. En la línea 37 buscamos cual es el último caracter y después damos la respuesta que corresponda.

Entrada:	on?
Desarrollo:	on? n= 3 p  a   +     d  1  3  0;  2 3 1  2  3  0;  2 3 2  3  3  0;  2 3 3 s[3]= '?'
Salida:	Yes

Entrada:	This is UNFAIR!
Desarrollo:	This isUNFAIR! n= 14 p  a   +                  d  1 14 10;  2 3  4 5 6  7 8 9 10 11 12 13 14 1 12 10  9;  2 3  4 5 6  7 8 9 10 12 12 13 14 1  8  6  6;  2 3  4 5 6  8 8 9 10 12 12 13 14 1  2 14  7;  2 3  4 5 6  8 8 9 10 12 12 13 14 2 12  9  8;  2 3  4 5 6  8 8 9 12 12 12 13 14 2  9  6  0;  2 3  4 5 6  9 8 9 12 12 12 13 14 2 12  6  6;  2 3  4 5 6 12 8 9 12 12 12 13 14 2  6  4  3;  2 3  4 6 6 12 8 9 12 12 12 13 14 2  2 13  0;  2 3  4 6 6 12 8 9 12 12 12 13  2 2  3 13  3;  2 3  4 6 6 12 8 9 12 12 12 13  3 2 13  6  2;  2 3  4 6 6 13 8 9 12 12 12 13  3 2  6  3  0;  2 3  6 6 6 13 8 9 12 12 12 13  3 2 13  3  0;  2 3 13 6 6 13 8 9 12 12 12 13  3 2  3  3  0;  2 3  3 6 6 13 8 9 12 12 12 13  3 2 s[3]= 'i'
Salida:	No comments

En el programa que acabamos de hacer, estamos simulando (con algunas optimizaciones) el comportamiento del problema. Otra forma de obtener el resultado es mediante la siguiente fórmula recursiva:
f(n) = (f(n-1) + m) mod n
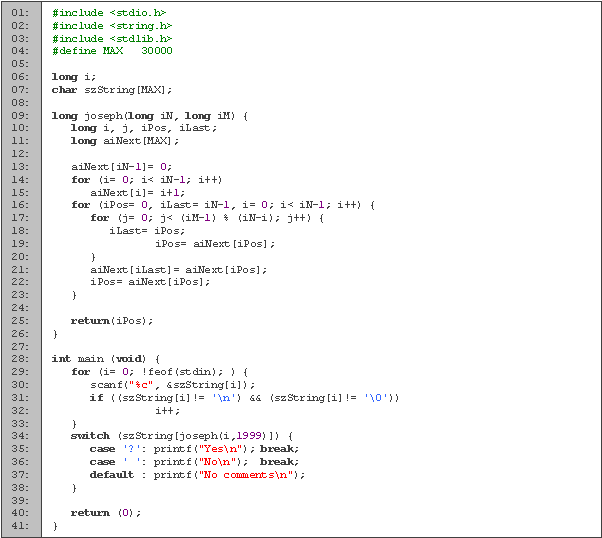
Donde n es la cantidad de personas en el círculo, y m es cada cuanto alguien va a ser eliminado. Empleando esta fórmula, obtenemos el siguiente código:


La función se llama igual que la anterior, y acepta los mismos parámetros. Declaramos en la línea 2 las variables a usar, i para el ciclo y r para el resultado. Inicializamos en resultado a cero, y en cada iteración calculamos el resultado con un elemento más. En la línea 7 devolvemos el resultado.

Como en la primera implementación estamos simulando, es más útil cuando se nos presenta una variación del problema. Por ejemplo, podemos obtener en que orden fueron eliminados, cuantos y quienes sobran después de cierto número de eliminados, y otras variaciones más.

Entrada:	on?
Desarrollo:	on? n= 3 r= 0, 1, 2, 3 s[3]= '?'
Salida:	Yes

Entrada:	This is UNFAIR!
Desarrollo:	This isUNFAIR! n= 14 r= 0, 1, 2, 3, 2, 1, 2, 6, 5, 6, 5, 2, 9, 6, 3 s[3]= 'i'
Salida:	No comments

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	17-Mar-2006	0.203	0.001	0.020	0.984	338
C	18-Mar-2006	0.109				274
Pascal	16-Mar-2006	0.015				262
C	18-Mar-2006	0.015				162

Valladollid:

Zhejiang: