Lo que deseamos mejorar mediante estas estructuras es el orden y forma en que debemos procesar los datos. Cambiando la forma en que guardamos los datos, el orden en que los utilizamos, el método para agregarlos o quitarlos, o alguna otra operación que realicemos con ellos, podemos encontrar mejores implementaciones para resolver un problema. A continuación veremos tres estructuras de datos básicas: pilas, colas y listas enlazadas.
En las pilas (también conocidas como stacks o FILO – first in, last out) lo que queremos es procesar los datos en orden inverso, esto es, primero procesamos los últimos datos que añadimos y hasta llegar a los iniciales. Una forma fácil de visualizarlo es mediante tortillas: al irlas calentando, se van apilando por lo que las primeras que se calentaron quedan abajo y son las últimas en ser comidas. La importancia de las pilas es que se utilizan implícitamente en cualquier programa recursivo (como en las búsquedas en profundidad). También podemos ver el uso de pilas en el algoritmo de Graham Scan (sección 7.6).
En las colas (también conocidas como queues, buffers o FIFO – first in, first out) los primeros elementos que entran son los primeros en ser procesados. Esto lo podemos ver en las filas en los bancos: los primeros que se forman son los primeros en ser atendidos (generalmente). Algunos ejemplos de su uso son en la escritura de números grandes (sección 6.3) y en las búsquedas en amplitud (como en la sección 9.4).
Una lista es simplemente un arreglo en el cual vamos agregando y sacando datos. En su forma más sencilla, una lista puede ser un arreglo. Uno de los problemas con los arreglos es que si queremos agregar un dato en medio, tenemos que recorrer todas las casillas que se encuentran a partir de esa posición un lugar. Esto se soluciona mediante listas enlazadas, en las cuales por cada casilla tenemos dos datos: el valor de la casilla y la posición de la siguiente casilla. Para agregar o quitar datos, solo tenemos que cambiar cual es la siguiente casilla. Si tenemos además del siguiente elemento también sabemos la posición del anterior, obtenemos una lista doblemente enlazada. Si hacemos que el último elemento este enlazado con el primero, obtenemos una lista circular. Este tipo de estructura las utilizamos en la sección 5.7, en la primera implementación.
Las listas enlazadas comúnmente se implementan mediante punteros y utilizando memoria dinámica. Sin embargo, a veces es conveniente utilizar un arreglo en lugar de memoria dinámica y enteros en lugar de punteros, ya que es más sencillo de implementar y de corregir, lo cuál es importante dentro de un concurso.
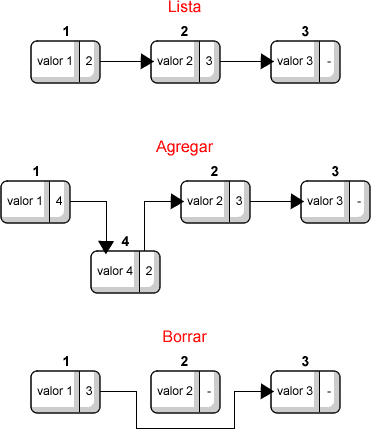 |
| Figura 11.1: Ejemplo de una lista enlazada y de las operaciones de agregar y borrar. |
Problema ejemplo
Balanceo de Paréntesis
Problema
Tienes una cadena que consiste en paréntesis () y []. Decimos que una cadena de este tipo es correcta si:
- La cadena está vacía.
- Si a y b son cadenas correctas, ab también es correcta.
- Si a es correcta, (a) y [a] también lo son.
Entrada
El archivo de entrada contiene un entero positivo n y una serie de n cadenas con paréntesis () y []. Se tiene una cadena por cada línea.Salida
Una serie de respuestas “Yes” o “No”, correspondiendo a si es correcta o no la cadena.Solución: Guardamos los paréntesis que abren en una pila. Cada que encontremos alguno que cierre, revisamos si lo hace de manera correcta. En caso de que sí lo haga, decrementamos el tamaño de la pila. Si al final del programa la pila está vacía y todos los paréntesis cerraron correctamente, entonces la cadena es correcta; sino, es incorrecta.
Código
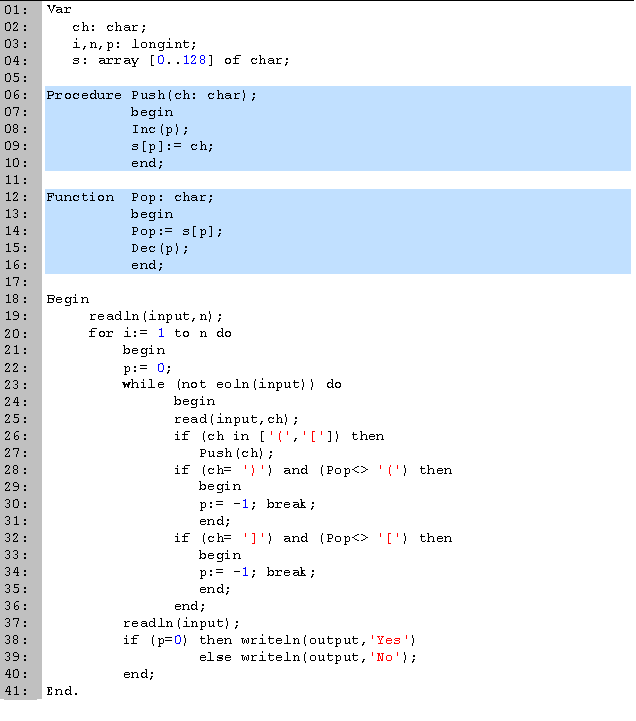
Empezamos declarando las variables que vamos a utilizar (líneas 1 a 4). Las cadenas las vamos a leer caracter por caracter a través de ch, para guardar la pila utilizaremos el arreglo s, y p para saber cual es la posición del último elemento en la pila. El entero i lo usaremos en ciclos y n para saber cuantos casos debemos procesar.
En seguida tenemos el procedimiento push (líneas 6 a 10) y la función pop (líneas 12 a 16), que nos sirven para meter y sacar datos de la pila. Para guardar un dato, se lo mandamos como parámetro a push, donde incrementamos la posición del último elemento y guardamos en esta posición al parámetro. Para obtener un dato, llamamos a la función pop, en la cual devolvemos el valor del último dato en la pila y decrementamos la posición del último dato. En ningún momento estamos revisando si la pila está llena o vacía, por lo que debemos tener cuidado al usarla (o agregar dichas verificaciones).
La parte principal del código la tenemos entre las líneas 18 y 41. Empezamos leyendo la cantidad de casos (línea 19). Para cada caso, leemos caracter por caracter hasta llegar al fin de línea. En la línea 22 inicializamos el tope de la pila. Cuando leemos un paréntesis que abre, lo agregamos a la pila (líneas 26 y 27). Si encontramos uno que cierra, sacamos un dato de la pila y revisamos si cierra correctamente (líneas 28 a 35); en caso de que no lo haga, ponemos la posición de la pila a una posición cualquiera (distinta de cero) y nos salimos. Al final, revisamos si la cadena es válida de acuerdo a si la pila termino vacía o no.Caso ejemplo
| Entrada: |
2 ([]) (([()]))) |
| Desarrollo: |
ch p s[] ( 0, [ 1, ( ] 2, ([ ) 1, ( 0 ( 0, ( 1, ( [ 2, (( ( 3, (([ ) 4, (([( ] 3, (([ ) 2, (( ) 1, ( ) 0, -1 |
| Salida: |
Yes No |
Código en C
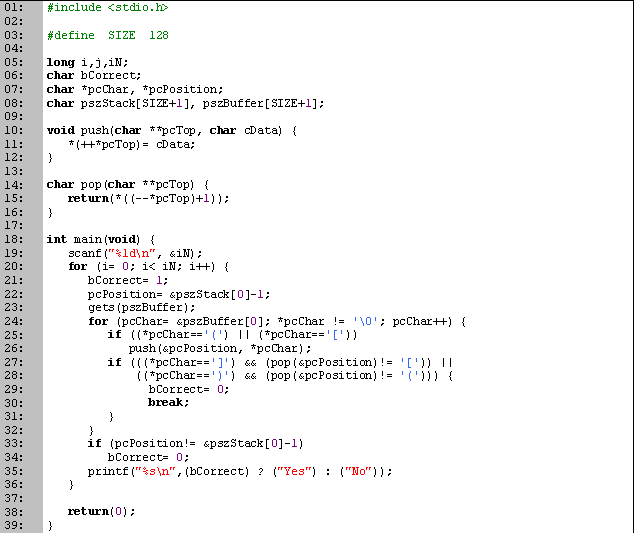
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 5-May-2006 | 0.510 | 0.027 | 0.338 | 72.670 | 324 |
| C | 13-Jun-2006 | 0.135 | 388 | |||
Otros problemas
El Judge:
 Solución de ecuaciones lineales (Gauss-Jordan) Solución de ecuaciones lineales (Gauss-Jordan) |
 Otros Temas |
Árboles binarios  |