Una de las principales desventajas de las listas enlazadas es que si queremos buscar un dato, tenemos que recorrer todo el arreglo. Esto también es problema cuando queremos agregar o quitar un dato, ya que tenemos que buscar primero la posición donde realizaremos la operación.
Este inconveniente lo podemos resolver utilizando árboles binarios. La idea básica de este tipo de estructura de datos es crear un árbol en el cual cada vértice tiene a lo más dos hijos (comúnmente llamados izquierdo y derecho). Los vértices tienen la propiedad de que todos los datos de la ramificación izquierda son menores al del vértice, mientras que los de la derecha son mayores. Los que sean iguales los podemos mandar a cualquiera de los dos lados, pero siendo consistentes.
Para construir un árbol binario, agregamos un vértice a la vez, considerando la propiedad del árbol binario. Si el vértice que vamos a agregar es menor a la raíz, entonces lo mandamos a la rama izquierda; en caso de que sea mayor, a la derecha. Esto lo repetimos hasta que podamos colocar al vértice como una hoja. Podemos buscar datos utilizando una metodología similar.
La forma más común de procesar los datos en un árbol binario es mediante una búsqueda en profundidad. De acuerdo a la forma en que realicemos esta búsqueda, surgen los recorridos pre-orden, orden y post-orden.
En los recorridos en pre-orden, primero procesamos el dato, después visitamos la rama izquierda y terminamos recorriendo la rama derecha. Para recorrer en orden, procesamos los datos después de visitar los vértices izquierdos pero antes de los derechos. Por último, para los recorridos en post-orden visitamos primero a los descendientes y terminamos procesando el vértice.
Los recorridos en orden tienen la ventaja de que los datos los procesamos del menor al mayor. Los recorridos en post-orden permiten borrar al árbol de forma consistente, esto es, al borrar el árbol nos deshacemos primeros de las hojas, por lo que no se pierden enlaces.
Es común que los árboles se enlacen mediante punteros y que cada que necesitemos un nuevo vértice utilizamos memoria dinámica para crearlo. Sin embargo, durante un concurso (o en cualquier aplicación simple en que sepamos la cantidad máxima de vértices) es más conveniente utilizar un arreglo en lugar de memoria dinámica y enteros que indiquen cuales casillas son los hijos para que el programa sea más sencillo de implementar y revisar.
Problema ejemplo
Nombre del Problema
Problema
Se va a elegir un nuevo Congreso para el estado MMMM. A cada miembro del congreso se le da una identificación con un número entero positivo durante el registro. Los números se distribuyeron de forma aleatoria, y es posible que existan huecos en la numeración. Las sillas en el congreso están acomodadas en forma de árbol. Cuando los miembros del congreso entraron al auditorio, se sentaron de la siguiente manera. El primero en llegar tomó la cabecera. Cada uno de los siguientes congresistas se dirigió a la izquierda si su número era menor al de la cabecera, o a la derecha en caso contrario. Después, si el asiento al que llegaba estaba vacío, lo tomaba; sino, el algoritmo se repetía: el congresista se dirigía a la izquierda o a la derecha de acuerdo a si su número era menor o no. La siguiente imagen muestra un ejemplo de cómo quedarían sentados los congresistas si entraran al auditorio en el siguiente orden: 10, 5, 1, 7, 20, 25, 22, 21, 27. 
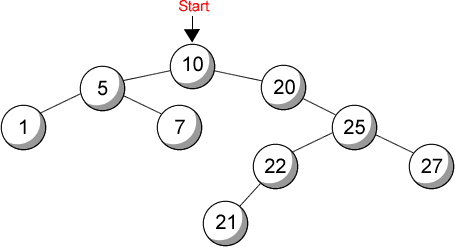
Durante la primera sesión, el congreso decidió mantener el mismo orden en el futuro. Después se decidió el orden en que los congresistas tomarían la palabra para dar sus discursos. Si el número de la sesión era impar, entonces los miembros del congreso tomarían la palabra en el siguiente orden: primero en congresista a la izquierda, después a la derecha y por último el central. Si la sesión era par, el orden cambiaba: primero a la derecha, después a la izquierda y por último el central. Para el ejemplo, en una sesión impar el orden sería: 1, 7, 5, 21, 22, 27, 25, 20, 10; mientras que para una par: 27, 21, 22, 25, 20, 7, 1, 5, 10.
Determina el orden de los discursos para una sesión par, si cuentas con el orden para una sesión par.
Entrada
La primera línea de la entrada contiene a n – la cantidad de congresistas. Las siguientes líneas tienen n enteros – el número de identificación de los miembros del congreso, ordenados de acuerdo a una sesión impar.La cantidad de miembros en el congreso no excede a 3000. Los números de identificación no exceden a 60000.
Salida
La salida debe contener los números de identificación de los miembros del congreso, en el orden de una sesión par.Solución: Tenemos a las personas acomodadas en un árbol binario, y la forma en que dan su disertación es un recorrido en post-orden. Lo que nos piden es obtener el recorrido también en post-orden, pero yendo primero a la derecha y después a la izquierda.
Al estar los datos en post-orden, los primeros datos son las hojas del árbol (los datos que están más lejos de la raíz). Después de las hojas, lo siguientes datos son los vértices que serían hojas si los primeros no estuvieran. Y así sucesivamente hasta llegar a la raíz (último dato). Por esto, podemos reconstruir el árbol agregando los datos al revés de cómo los muestra la entrada.
Código
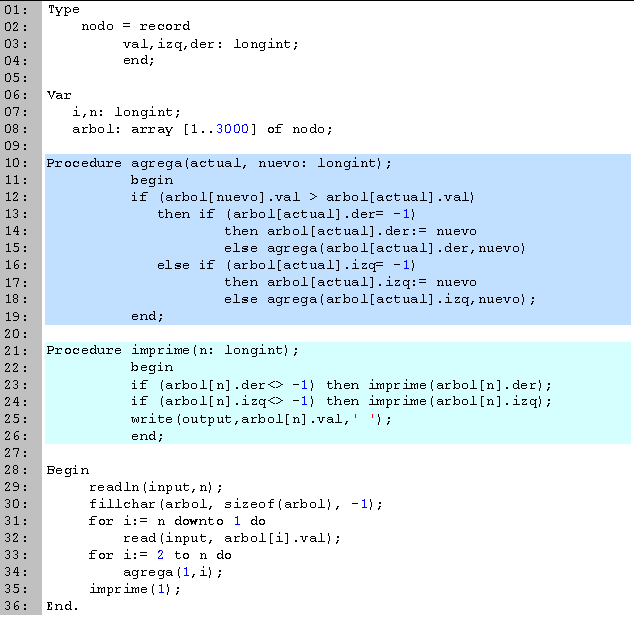
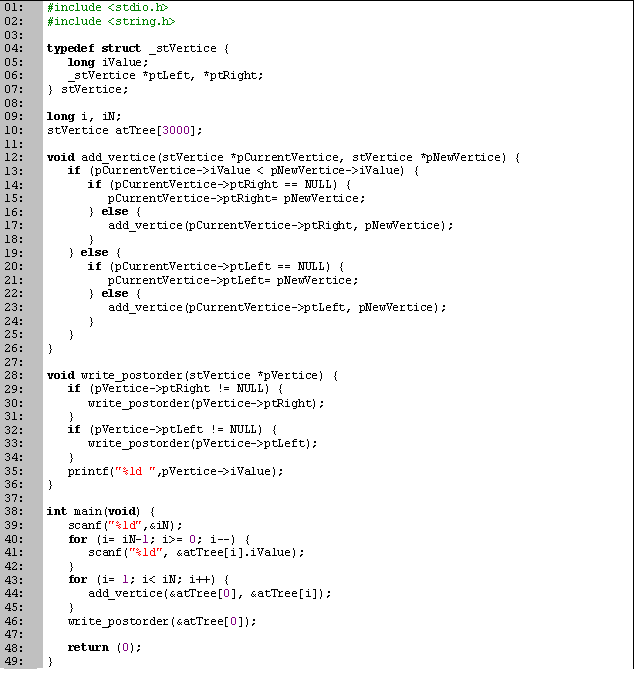
En las primeras tres líneas definimos el tipo de variable nodo, el cual utilizaremos para representar todos los vértices del árbol. Dentro de nodo tenemos tres campos: val que es el valor del vértice (en este caso, el número de identificación), izq y der que nos indican cuales son los hijos del vértice actual.
A continuación declaramos las variables globales que vamos a utilizar. El entero n lo utilizamos para leer la cantidad de personas, i es una variable para los ciclos y el arreglo arbol lo utilizaremos para guardar los valores de los vértices del árbol.
En seguida tenemos el procedimiento agrega (líneas 10 a 19), el cual añade un nuevo vértice al árbol. Si el nuevo dato es mayor al actual, entonces lo pasamos a la derecha, en caso contrario lo mandamos a la izquierda (línea 12). Esto lo seguimos repitiendo hasta que el dato lo podamos colocar como hoja (líneas 13 y 16), donde los anexamos.
En el procedimiento imprime (líneas 21 a 26) imprimimos los valores de todos los vértices del árbol, utilizando un recorrido en post-orden, pero visitando derecha y luego izquierda, en lugar de izquierda y luego derecha. Para esto, empezando desde la raíz hacemos lo siguiente: si existe una rama hacia la derecha entonces la visitamos (línea 23), después hacemos lo mismo con la izquierda (línea 24) y por último imprimimos el dato que contiene el vértice actual (línea 25). Para implementar un recorrido en orden o pre-orden sólo hay que subir la escritura uno o dos lugares, respectivamente.
Estos dos procedimientos se pueden realizar de forma iterativa, con lo que obtenemos una ligera ganancia en eficiencia.La parte principal del código la tenemos entre las líneas 28 y 36. Empezamos leyendo en n la cantidad de datos que va a contener el árbol (línea 29). Inicializamos todo el arreglo a un valor arbitrario que nos indique que no se tienen ramificaciones (en este caso, -1). Después leemos todos los datos y los guardamos en orden opuesto (líneas 31 y 32). En seguida construimos el árbol agregando un vértice a la vez (línea 33). Y por último mandamos a imprimir el árbol en post-orden.
Caso ejemplo
| Entrada: |
9 1 7 5 21 22 27 25 20 10 |
| Desarrollo: |
1 2 3 4 5 6 7 8 9 val[]= 10, 20, 25, 27, 22, 21, 5, 7, 1 actual nuevo 1 2 20 > 10: derecha izq[]= -1 -1 -1 -1 -1 -1 -1 -1 -1 der[]= 2 -1 -1 -1 -1 -1 -1 -1 -1 1 3 25 > 10: derecha 2 3 25 > 20: derecha izq[]= -1 -1 -1 -1 -1 -1 -1 -1 -1 der[]= 2 3 -1 -1 -1 -1 -1 -1 -1 1 4 27 > 10: derecha 2 4 27 > 20: derecha 3 4 27 > 25: derecha izq[]= -1 -1 –1 -1 -1 -1 -1 -1 -1 der[]= 2 3 4 -1 -1 -1 -1 -1 -1 1 5 22 > 10: derecha 2 5 22 > 20: derecha 3 5 22 < 25: izquierda izq[]= -1 -1 5 -1 -1 -1 -1 -1 -1 der[]= 2 3 4 -1 -1 -1 -1 -1 -1 1 6 21 > 10: derecha 2 6 21 > 20: derecha 3 6 21 < 25: izquierda 5 6 21 < 22: izquierda izq[]= -1 -1 5 -1 6 -1 -1 -1 -1 der[]= 2 3 4 -1 -1 -1 -1 -1 -1 1 7 5 < 10: izquierda izq[]= 7 -1 5 -1 6 -1 -1 -1 -1 der[]= 2 3 4 -1 -1 -1 -1 -1 -1 1 8 7 < 10: izquierda 7 8 7 > 5: derecha izq[]= 7 –1 5 -1 6 -1 -1 -1 -1 der[]= 2 3 4 -1 -1 -1 8 -1 -1 1 9 1 < 10: izquierda 7 9 1 < 5: izquierda izq[]= 7 –1 5 -1 6 -1 9 -1 -1 der[]= 2 3 4 -1 -1 -1 8 -1 -1 imprime n= 1, derecha n= 2, derecha n= 3, derecha n= 4, imprime: 27 n= 3, izquierda n= 5, izquierda n= 6, imprime: 21 n= 5, imprime: 22 n= 3, imprime: 25 n= 2, imprime: 20 n= 1, izquierda n= 7, derecha n= 8, imprime: 7 n= 7, izquierda n= 9, imprime: 1 n= 7, imprime: 5 n= 1, imprime: 10 |
| Salida: | 27 21 22 25 20 7 1 5 10 |
Información Adicional
En general, esperamos que el número de vértices que debemos recorrer para encontrar un dato sea de Q(lgn). Ésta es una gran ventaja comparados con las listas. No obstante, en algunos casos el árbol degenera en una lista por lo que su peor caso es O(n) (como cuando todos los datos están en orden ascendente antes de insertarlos al árbol).
Podemos solucionar esto balanceando el árbol. Decimos que un árbol está balanceado (o equilibrado) cuando mantiene una altura mínima. Poder mantener está propiedad de manera eficiente y dinámica es complicado y puede ser manejado de distintas formas, con lo que surgen los montículos (sección 3.4), los montículos de Fibonacci, los árboles rojo-negro, los árboles-B, entre otros (no todos son binarios).
Código en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 26-Abr-2006 | 0.125 | 0.001 | 0.046 | 0.370 | 214 |
| C | 26-Abr-2006 | 0.015 | 198 | |||
Otros problemas
Valladollid:
Estructuras de datos básicas (Pilas, Colas y Listas Enlazadas)
