Los algoritmos ávidos son algoritmos en los que tomamos decisiones locales para llegar a una cantidad óptima global. En este sentido, son parecidos a los de programación dinámica. La diferencia es que para resolver un problema con programación dinámica, tomamos en cuenta todas las soluciones para los subproblemas anteriores y con esto encontramos la solución óptima; mientras que para resolver un problema mediante un algoritmo ávido, sólo tomamos la solución óptima del subproblema anterior y con esto calculamos la óptima actual (por lo que no necesitamos guardar datos).
Esto es, empezamos por el caso más sencillo y en cada paso tomamos la decisión que resulte más eficiente en ese momento, con lo que esperamos llegar a una solución óptima global, sin reconsiderar opciones.
Los algoritmos ávidos encuentran las soluciones mucho más rápido que por programación dinámica, y muchas veces que por cualquier otro método. El problema es que, aunque el enfoque es generalmente fácil de implementar, en la mayoría de las ocasiones falla por no tomar en cuenta todas las combinaciones. Es por esto que no es conveniente utilizarlo a menos de que estemos convencidos de que funciona (preferentemente con una demostración).
Entre los algoritmos más conocidos que utilizan un enfoque ávido, se encuentran los de Dijkstra, Prim y Kruskal (secciones 10.4 y 10.6) que funcionan en gráficas.
A veces son utilizados para diseñar algoritmos heurísticos para problemas NP-completo, con lo que podemos obtener una buena aproximación de la solución en poco tiempo. De acuerdo a la complejidad del problema, un enfoque ávido nos puede dar una aproximación suficientemente buena o, si queremos una respuesta óptima, podemos utilizarla para realizar podas en una búsqueda exhaustiva.
Problema ejemplo
Conferencia
Problema
Es común que las conferencias científicas estén divididas en varias secciones simultáneas. Por ejemplo, puede haber una sección para computación en paralelo, otra para visualización, otra para compresión de datos, y así sucesivamente.Es obvio que se necesita realizar el trabajo de varias secciones de forma simultánea para reducir el tiempo de la conferencia y tener suficiente tiempo para las comidas, tomar café, y las discusiones informales. Sin embargo, es posible que se estén dando ponencias interesantes de forma simultánea en distintas secciones.
Un participante ha escrito una tabla con los horarios de todas las ponencias que le interesan. Te ha pedido que encuentres la cantidad máxima de ponencias a los que puede asistir.
Entrada
La primera línea contiene el número 1 ≤ n ≤ 100000, que es la cantidad de ponencias interesantes. Cada una de las siguientes n líneas contiene a dos enteros ts y te separados por un espacio (1 ≤ ts < te ≤ 30000). Estos números corresponden al horario en que las ponencias empiezan y terminan. Los horarios están dados en minutos a partir del inicio del evento.Salida
Deberás escribir la cantidad máxima de ponencias a las que el participante puede asistir. El participante no puede estar en dos ponencias al mismo tiempo, y a las ponencias a las que asista tienen que estar separadas por un minuto por lo menos. Por ejemplo, si una ponencia termina en el minuto 15, la siguiente ponencia a la que puede asistir debe empezar al minuto 16 o después.Solución: Si tenemos dos o más ponencias que terminan a la misma hora, sólo consideramos la que empieza más tarde (por lo que dura menos). Una vez hecho esto, tomamos los datos ordenados por lo hora a la que terminan (de menor a mayor), y recorremos los datos incrementando un contador cada que podamos tomar una conferencia.
Código
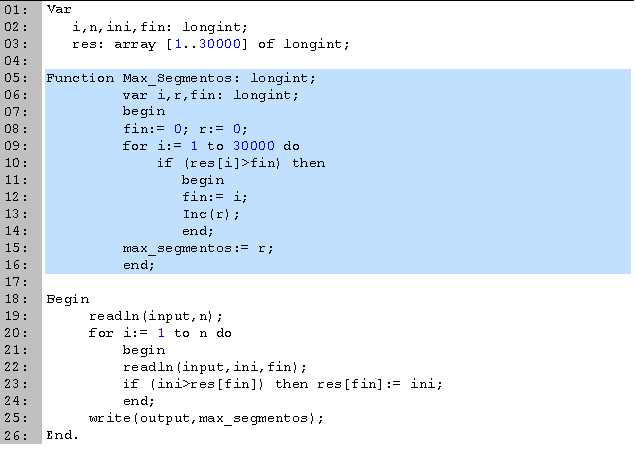
En las primeras tres líneas definimos las variables que vamos a utilizar. En n leemos la cantidad de ponencias, i lo usamos para los ciclos, ini y fin para leer el inicio y final de las ponencias, y el arreglo res para ordenar los datos.
Los datos los ordenaremos en un arreglo, de manera similar a como lo haríamos con una ordenación por conteo, ya que el valor máximo de n es significativamente mayor al máximo de fin. En la k-ésima casilla de res vamos a guardar el valor de la hora a la que inicia la ponencia que termina a las k horas.
En seguida buscamos la cantidad máxima de segmentos que no se traslapan (líneas 5 a 16). El entero i lo usamos para ciclos, r para guardar el resultado y fin para saber donde termina el último segmento que utilizamos. Empezamos inicializando r y fin a cero. Buscamos en el intervalo por el primer segmento cuyo inicio sea posterior a fin (el siguiente segmento que no se sobrepone). Una vez que lo encontramos, incrementamos el resultado y le asignamos a fin el final de este segmento. Podemos obtener los valores máximo y mínimo de los finales de los segmentos para no tener que recorrer valores innecesarios dentro del ciclo, aunque no es una mejora significativa.
La parte principal del código la tenemos entre las líneas 18 y 26. Empezamos leyendo la cantidad de ponencias (línea 19). Para cada ponencia, leemos la hora de entrada y salida (línea 22) y si la hora de entrada es mayor a la que teníamos, la actualizamos (línea 23). Terminamos escribiendo el número máximo de ponencias (segmentos) que no se empalman (línea 25).Caso ejemplo
| Entrada: |
5 3 4 1 5 6 7 4 5 1 3 |
| Desarrollo: |
res[] 1 2 3 4 5 6 7 3 4 -, -, -, 3, -, -, - 1 5 -, -, -, 3, 1, -, - 6 7 -, -, -, 3, 1, -, 6 4 5 -, -, -, 3, 4, -, 6 1 3 -, -, 1, 3, 4, -, 6 res[i] fin r 0, 0 1: - 0, 0 2: - 0, 0 3: 1 > 0, 1 4: 3 = 3, 1 5: 4 > 3, 2 6: - 5, 2 7: 6 > 5, 3 |
| Salida: | 3 |
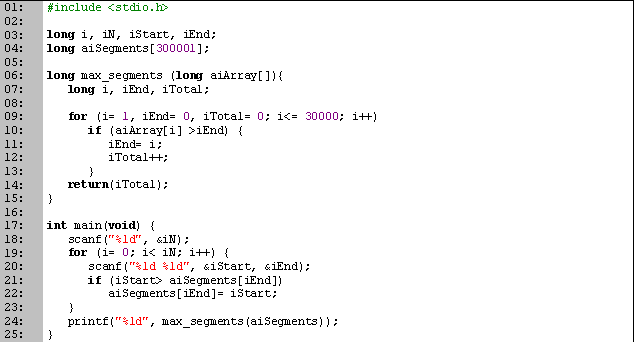
Código en C
Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 28-Abr-2006 | 0.046 | 0.031 | 0.130 | 0.984 | 286 |
| C | 28-Abr-2006 | 0.046 | 266 | |||
Otros problemas
Valladollid:
Ural:
 Árboles binarios
Árboles binarios
