Al igual que con programación dinámica y algoritmos ávidos, buscamos resolver un problema a través de sus partes. La idea básica es ir dividiendo el problema en partes (generalmente dos) e intentar resolverlas. Si las partes son todavía demasiado complejas, las volvemos a partir. Repetimos esto recursivamente hasta que podamos resolver los subproblemas de manera directa. Una vez que tenemos estas respuestas, las juntamos para obtener la solución general.

Un problema que pueda ser resuelto por divide y vencerás, muchas veces es también posible resolverlo mediante programación dinámica con un enfoque “arriba-abajo”, o viceversa. Lo importante al decidir cual utilizar es si existen empalmes o repeticiones en los subproblemas.

El diseño de la solución mediante divide y vencerás involucra tres pasos:

• Dividimos el problema en subproblemas, tratando de que no existan empalmes y forzando a que cada subproblema sea menor al problema original.
• Resolvemos los subproblemas. Si los subproblemas son suficientemente pequeños, encontramos la solución directa; en caso contrario, resolvemos recursivamente con el algoritmo.
• Combinamos las soluciones de los subproblemas en una sola.

Aunque esta es la forma general de la técnica de diseño, no siempre es necesario utilizar todos los pasos. Por ejemplo, al realizar una ordenación rápida de Hoare, no necesitamos combinar las soluciones, ya que al terminar de resolver los subproblemas, el problema general también estará resuelto.

Una variación de esta técnica se conoce como decrementa y vencerás. La diferencia básica es que al dividir el problema en subproblemas, sólo debemos resolver uno de estos y podemos desechar a los demás. Como al final terminamos resolviendo sólo un subproblema, tampoco tenemos que combinarlos.

Varios de los problemas clásicos que se pueden resolver mediante divide y vencerás son algoritmos vistos en alguna otra sección. Por ejemplo: ordenación rápida de Hoare y exponenciales con módulo para divide y vencerás; búsqueda binaria y bisección para decrementa y vencerás. Esta técnica también resulta útil en varios problemas de geometría computacional, como para encontrar cascos convexos o para encontrar los dos puntos más cercanos en un plano.




Solución: Este problema es muy similar al de la sección 3.2, pero con la diferencia de que el valor del tamaño máximo del arreglo es muy grande por lo que un algoritmo O(n²) tardaría demasiado.

Como mencionamos en esa sección, podemos resolver el problema sin necesidad de ordenar el arreglo, recorriéndolo y contando cuantos elementos que ya pasamos son menores al actual. Esto lo podemos realizar fácilmente mediante dos ciclos, pero no estaríamos mejorando el tiempo. Existen alternativas para resolverlo de forma eficiente (por ejemplo, mediante árboles balanceados) pero resultan complejas.

Otra alternativa es ordenar los datos y contar cuantas casillas de diferencia existen entre la casilla original y la final. Podemos ver como al hacer un intercambio, un valor “sube” mientras el otro “baja”, por lo que al revisar la diferencia podemos contar sólo los que quedaron más arriba o los que quedaron más abajo (o contar ambos y dividir el resultado entre dos).

Para ordenar los datos, vamos a utilizar la ordenación por mezclas, la cual fue inventada por John von Neumann en 1945 y es una buena ejemplificación del diseño mediante divide y vencerás. Siguiendo los pasos los pasos que vimos anteriormente, podemos ordenar un arreglo siguiendo los siguientes pasos:

• Dividimos el arreglo en dos partes (preferentemente iguales, o de diferencia mínima).
• Ordenamos los subarreglos.
• Juntamos los subarreglos ordenados en uno solo.

La forma en que mezclemos los dos subarreglos en uno es muy importante, ya que de esto depende la eficiencia del algoritmo. Buscamos poder unirlos en tiempo lineal, con lo que tendríamos un algoritmo O(nlgn).




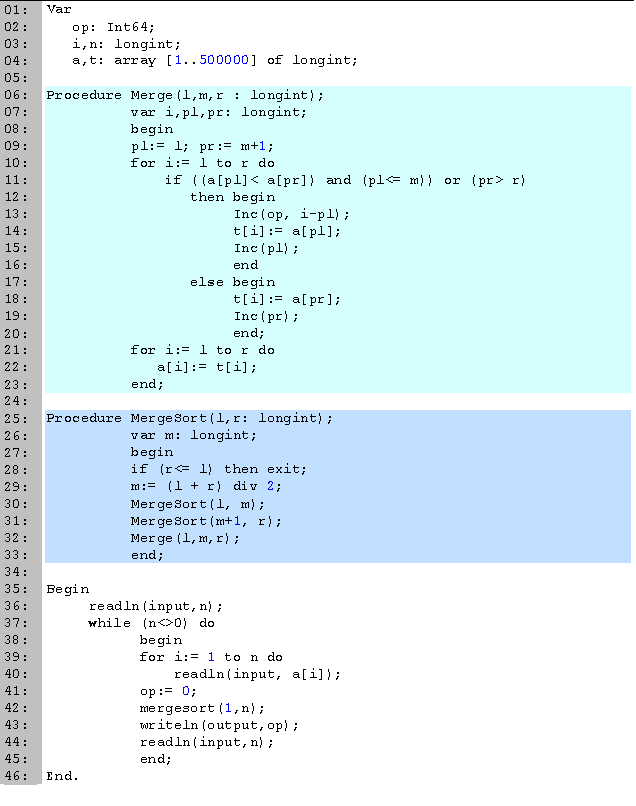
Comenzamos declarando en las primeras 4 líneas las variables que vamos a utilizar. La única variable que vamos a manejar que no está definida en el problema es t, un arreglo que usaremos para guardar datos temporales. Este arreglo sólo lo utilizamos en el procedimiento merge, por lo que podríamos definirlo dentro de él. La razón por la que no lo hacemos es porque vamos a llamar a la función muchas veces y el arreglo es grande, por lo que cada vez que llamáramos a la función tendría que volver a crear el arreglo. La variable op es de tipo Int64, ya que la cantidad máxima de cambios es 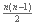 y para n = 500000 el resultado excede la capacidad de un longint.

La ordenación por mezclas está compuesta por dos procedimientos: merge (líneas 6 a 23) que combina los subarreglos en uno, y mergesort (líneas 25 a 33) que es donde resolvemos recursivamente el problema.

En mergesort, tenemos como parámetros los enteros l y r que nos indican el intervalo del arreglo que vamos a ordenar. Si estos dos valores son iguales, entonces sólo es una casilla, la cual podemos considerar ordenada; si el segundo es menor el primero, es una entrada no válida, por lo cual tampoco tenemos que ordenar (línea 28). En la variable m calculamos la posición de la casilla que se encuentra en medio del intervalo (línea 29), y después mandamos ordenar recursivamente las dos mitades (líneas 30 y 31). Terminamos uniendo las dos subpartes en una sola.

En ocasiones esta parte se modifica para que cuando los subproblemas sean suficientemente pequeños (digamos un tamaño menor a veinte), en vez de esperarnos a llegar a subproblemas de tamaño uno, utilizamos alguna otra ordenación más sencilla como lo puede ser por inserción. Esto lo vuelve más eficiente, aunque no cambia la complejidad.

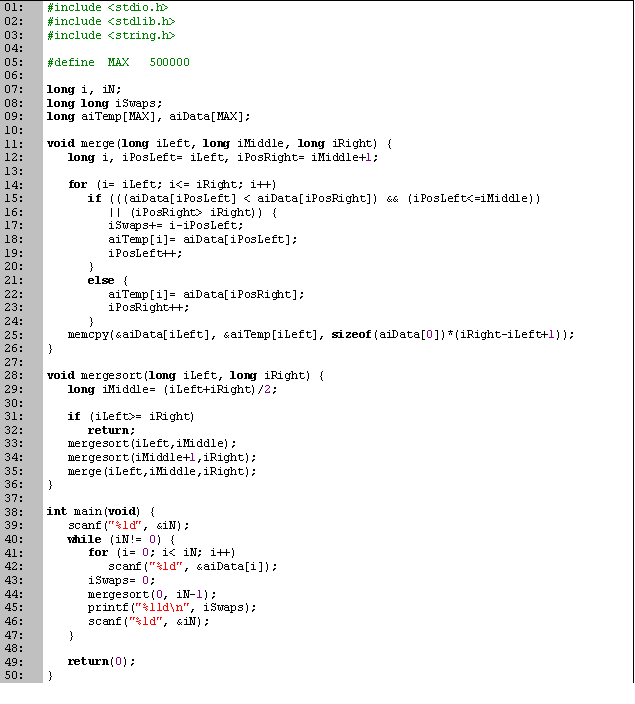
En merge es donde combinamos los dos subarreglos. El primero se encuentra entre l y m, y el segundo entre m+1 y r, ambos dentro del arreglo donde se encuentran los datos (a). Para juntar los dos, vamos a necesitar el arreglo auxiliar t. Declaramos los enteros pl y pr para saber en que casilla nos encontramos en cada uno de los subarreglos. Para cada casilla en el intervalo, tomamos el menor entre la posición actual en los dos subarreglos, teniendo cuidado de que todavía queden datos en estos. Una vez que decidimos que dato tomar, lo asignamos e incrementamos la posición en el subarreglo (líneas 14 y 15, y 18 y 19). Podemos ver como pl ≤ i  ≤ pr, por lo que la cantidad de casillas que se mueven en una dirección las podemos contar al mover un dato de cualquiera de los dos subarreglos (en este caso, del primero, línea 13). Al final terminamos pasando los datos del arreglo temporal al de datos (líneas 21 y 22).

La parte principal del código la tenemos entre las líneas 35 y 46. Empezamos leyendo la cantidad de datos a procesar. Mientras sea distinta de cero, leemos los datos del arreglo (líneas 39 y 40), los ordenamos (línea 43), e imprimimos la cantidad de intercambios que serían necesarios (línea 44). Terminamos leyendo la cantidad de datos del nuevo caso (línea 44).

Entrada:	5 9 1 0 5 4 0
Desarrollo:	a[]               9 1 0 5 4  l  r  1  5;        9 1 0 5 4;  1  3;        9 1 0 5 4;  1  2;        9 1 0 5 4;  1  1;        9 1 0 5 4;  2  2;        9 1 0 5 4; merge(1,1,2)  1 9 0 5 4; op= 1  3  3;        1 9 0 5 4; merge(1,2,3)  0 1 9 5 4; op= 3  4  5;        0 1 9 5 4;  4  4;        0 1 9 5 4;  5  5;        0 1 9 5 4; merge(4,4,5)  0 1 9 4 5; op= 4 merge(1,3,5)  0 1 4 5 9; op= 6
Salida:	6

Una de las principales razones por la que la ordenación por mezclas no es tan utilizada, es porque necesita un arreglo auxiliar para combinar los subproblemas. Aunque existen formas de no utilizarlo, hacerlo es complejo y pierde eficiencia. Además de esto, la ordenación rápida de Hoare y la ordenación por montículos suelen ser más rápidos.

Aún así, la ordenación por mezclas tiene propiedades que son útiles en algunas ocasiones. A diferencia de las dos ordenaciones anteriores, la ordenación por mezclas es estable. También es útil al ordenar datos en paralelo, datos de lento acceso, o listas enlazadas.

Lenguaje	Fecha	Tiempos [s]				Memoria [Kb]
		Ejecución	Mejor	Mediana	Peor
Pascal	08-Jun-2006	1.437	0.172	1.600	8.687	4224
C	13-Jun-2006	1.268				4300

Valladollid: