Teniendo una función f(x), buscamos aquellos valores de x tales que f(x) = 0. A estos valores se le conoce como raíces, soluciones o ceros de la función. Aunque para ecuaciones de hasta orden cuarto podemos utilizar fórmulas para encontrar las raíces, en ecuaciones de orden mayor no siempre es posible, por ello la importancia de estos métodos. A continuación estudiaremos dos métodos que nos permiten encontrar una raíz para este tipo de ecuaciones.
El método de la bisección es un algoritmo que nos permite encontrar una raíz de la función que tengamos. Su funcionamiento es muy similar al de la búsqueda binaria, sólo que estamos utilizando valores continuos (infinitos) en lugar de discretos (finitos). Vamos a asumir que las funciones con las que trabajamos son continuas.
Sabemos que si la función f(x) atraviesa el eje x, en la intersección existe una raíz, por lo que poco antes de la raíz f(x) > 0 y poco después f(x) < 0 (o viceversa). Entonces, teniendo dos puntos a y b tales que f(a) y f(b) tienen signos opuestos, sabemos que debe haber una raíz en el intervalo [a, b] (por el Teorema del Valor Intermedio).
El algoritmo funciona de la siguiente forma: tomamos el punto medio entre a y b, al cual llamaremos c (
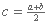 ). Si el valor de f(c) es cero, o está suficientemente cerca, tomamos a c como el valor de la raíz. En caso contrario, reemplazamos a a o b por c, de acuerdo al signo de f(c), de tal forma que los signos de f(a) y f(b) sigan siendo diferentes, y repetimos el método con el nuevo intervalo.
). Si el valor de f(c) es cero, o está suficientemente cerca, tomamos a c como el valor de la raíz. En caso contrario, reemplazamos a a o b por c, de acuerdo al signo de f(c), de tal forma que los signos de f(a) y f(b) sigan siendo diferentes, y repetimos el método con el nuevo intervalo.La principal ventaja de este método es que es muy confiable, ya que está garantizado que el método converge si los valores de f(a) y f(b) son de signos contrarios. La convergencia de este método es lineal, y su error absoluto después de n iteraciones es:
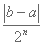
(Homenaje a Theodore Seuss Geisel)
El Gato en el Sombrero resultó ser una extraña creatura,
Hasta con su sombrero a rayas puede hacer alguna travesura.
Con un giro de la muñeca le quita la tapa.
¿Sabes que guarda el Gato dentro de su Sombrero?
Gatos más chicos, cada uno con sombrero desde luego.
Y cada uno de estos gatos repite lo mismo de la línea tres.
Excepto los más pequeños, que solo dicen “¿Por qué yo otra vez?”
Ya que los pequeñitos están obligados a limpiar el desastre,
Y al tener que hacerlo siempre, ¡quieren mandar todo al traste!
La cantidad de ayudantes dentro del sombrero de un gato (excepto por los más pequeños) es una cantidad constante n. La altura de los ayudantes es
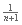 veces la altura del gato de cuyo sombrero salieron.
veces la altura del gato de cuyo sombrero salieron.La altura de los gatos más pequeños es 1; estos gatos son los que realizan todo el trabajo.
Todas las alturas son enteros positivos.
Dada la altura del primer gato y la cantidad de gatos que están trabajando (los de altura 1), encuentra la cantidad de gatos que no están trabajando (gatos de altura mayor a 1) y también las suma de las alturas de todos los gatos (la altura de poner a todos los gatos uno sobre de otro).
Un par de 0 indica el fin de la entrada.
Solución: Si denotamos a la cantidad de gatos trabajando como w, a la altura del primer gato como h, y a la cantidad de diferentes alturas como m, tenemos que:
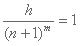
Ya conocemos los valores de h y w (nos los dan en la entrada), por lo que hay que encontrar los de m y n.
Despejando m de la primera ecuación:
lnw = mlnn
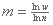
Despejando m de la segunda:
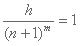
h = (n + 1)m
lnh = mln(n + 1)
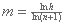
Igualando el recíproco de las dos ecuaciones:
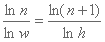
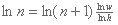
Haciendo
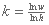 :
:n = (n + 1)k
Mediante algún método de obtención de raíces podemos encontrar el valor de n. Ya que tengamos el valor de n, podemos encontrar el de m en cualquiera de los dos despejes. Y una vez que tengamos los valores de m y n, podemos obtener la cantidad de gatos que no trabajan como:
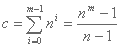
Y la suma de alturas de los gatos como:
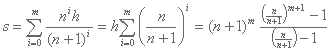
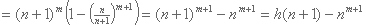
Nota: como los valores de m y n son enteros, también se pueden obtener utilizando propiedades aritméticas.

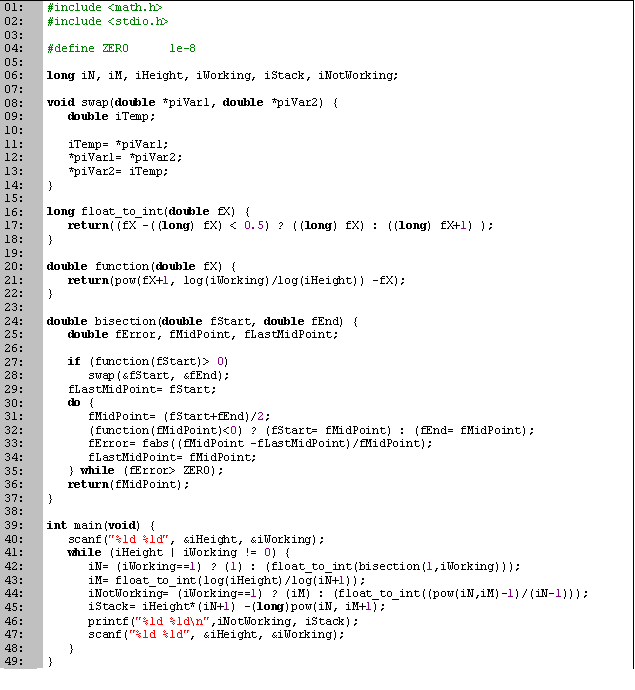
Las primeras dos líneas la utilizamos para definir la constante cero. Esta constante nos sirve para determinar cuando el error del algoritmo está en un rango aceptable (entre más precisión requiramos, será menor su valor). El valor de 10-8 es empírico y es útil en la mayoría de los problemas. Podemos utilizar valores menores y los métodos convergerán más rápido, pero posiblemente a un resultado erróneo. Después tenemos dos líneas (4 y 5) en las que declaramos las variables a utilizar, utilizando la misma notación que el problema y en la solución.
A continuación tenemos la función funcion (líneas 7 a 10), que es donde evaluamos f(x). En nuestro caso tenemos que n = (n + 1)k, por lo que la función que debemos evaluar es (n + 1)k -n = 0. Como Pascal no tiene función para evaluar potencias, hacemos eln(n + 1)k -n = 0, que es igual a ekln(n + 1) -n = 0, después sustituimos k por su valor y cambiamos n por x.
En seguida tenemos la función biseccion (líneas 12 a 27), que nos devuelve una raíz de la ecuación. Los parámetros ini y fin son los extremos del intervalo, y las variables error, pm y pma las utilizamos para calcular el error relativo, el punto medio y el punto medio anterior. El valor del pma lo inicializamos a cualquiera de los dos extremos (línea 15). Por simplicidad, vamos a utilizar a ini como el valor que evalúa a negativo. Si esto no se cumple, intercambiamos el valor con fin (líneas 16 a 19).
En cada iteración, calculamos el punto medio (línea 21), se lo asignamos a alguno de los extremos según corresponda (líneas 22 y 23), calculamos el error (línea 24), guardamos el punto medio (línea 25) y si estamos suficientemente cerca de la raíz, nos salimos. Algo importante es que en ningún momento revisamos si f(ini) y f(fin) evalúan a diferente signo, por lo que si son de signo iguales la función devolverá resultados erróneos.
| Entrada: |
216 125 0 0 |
| Desarrollo: |
ini pm fin f(pm) 1 125.000 63.000 1.000; -21.083 2 63.000 32.000 1.000; -8.880 3 32.000 16.500 1.000; -3.422 4 16.500 8.750 1.000; -1.017 5 8.750 4.875 1.000; 0.031 6 8.750 6.813 4.875; -0.475 7 6.813 5.844 4.875; -0.216 8 5.844 5.359 4.875; -0.091 9 5.359 5.117 4.875; -0.030 10 5.117 4.996 4.875; 0.001 11 5.117 5.057 4.996; -0.014 12 5.057 5.026 4.996; -0.007 13 5.026 5.011 4.996; -0.003 14 5.011 5.004 4.996; -0.001 15 5.004 5.000 4.996; 0.000 16 5.004 5.002 5.000; -0.000 17 5.002 5.001 5.000; -0.000 18 5.001 5.000 5.000; -0.000 19 5.000 5.000 5.000; -0.000 n= 5 m= ln(216)/ln(5+1)= 3 c= (5^3 -1)/(5 -1)= 31 s= 216(5+1) –5^(3+1)= 1296 –625= 671 |
| Salida: | 31 671 |
Nota: El método ejecuta más iteraciones, pero para fines demostrativos, sólo tomamos las que son significativas con tres decimales. La cantidad total de iteraciones es 32.
Algo que podemos apreciar es que hasta la iteración 10, los valores de pm siempre estaban acercándose a la raíz, pero en la 11ª se aleja un poco. Este es uno de los principales problemas de bisección, ya que si alguno de los extremos está cerca de la raíz y el otro esta alejado, el método no aprovecha al primero para encontrar más rápidamente la solución.
Otro método numérico ampliamente utilizado en la obtención de raíces es el de Newton (también conocido como Newton-Raphson o Newton-Fourier), principalmente porque es de los más rápidos.
Este método fue inventado por Isaac Newton en 1669. Sin embargo, la metodología era un tanto distinta a la que conocemos actualmente ya que era puramente algebraico. El método de Newton era muy similar al que utilizo Herón para calcular la raíz de 720. El método fue simplificado tiempo después por Raphson en 1690 y relacionado con el cálculo diferencial por Simpson en 1740.
Para encontrar una raíz en una función diferenciable mediante Newton, empezamos con una aproximación a la raíz de la ecuación, la cual tomamos como punto inicial. A continuación, en lugar de buscar la raíz de la ecuación, buscamos la raíz de la tangente que pasa por la aproximación. Como el cero de la tangente tiende a estar más cerca de la raíz, cambiamos nuestra aproximación por este valor. Repetimos hasta que obtenemos un valor suficientemente cercano a la raíz. Esto lo podemos calcular iterativamente de la siguiente forma:
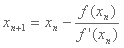
La convergencia de este algoritmo es cuadrada, con lo que la cantidad de dígitos correctos se duplica en cada iteración. Esto sucede cuando la raíz tiene multiplicidad uno, ya que en caso contrario, la convergencia es lineal (como en bisección).
Podemos arantizar que la convergencia del método siempre sea cuadrada haciendo unos cambios. Si reemplazamos a la función original f(x) por
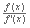 , obtenemos una nueva función que conserva las mismas raíces pero las reduce a multiplicidad uno. Realizando el cambio en la fórmula y despejando, obtenemos:
, obtenemos una nueva función que conserva las mismas raíces pero las reduce a multiplicidad uno. Realizando el cambio en la fórmula y despejando, obtenemos: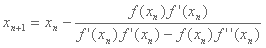
Aunque con este cambio ya no tenemos problemas con la multiplicidad, todavía podemos tener problemas de redondeo si la multiplicidad es mayor a dos (ya que la función y las dos derivadas tienden simultáneamente a cero). Otro inconveniente es que si la multiplicidad de la raíz ya era uno, estamos realizando cálculos innecesarios.

En esta función, tenemos como entrada el valor inicial que se acerca a la raíz y como salida el valor de la raíz aproximado con un error relativo menor a cero. Como variables utilizamos f, f1 y f2 para evaluar la función y sus dos derivadas, error para calcular el error relativa, ant para guardar el valor anterior y k que lo utilizamos de acuerdo a la solución del problema. Empezamos inicializando asignando el valor de k (línea 4). En cada iteración respaldamos el valor de x en ant (línea 6), evaluamos la función y sus derivadas (líneas 7 a 9), obtenemos la nueva aproximación (línea 10) y calculamos el error (línea 11). Repetimos esto hasta que nuestra solución este suficientemente próxima a la raíz.
A diferencia de bisección, Newton no siempre converge por lo que en ocasiones es conveniente poner un límite a la cantidad de iteraciones que puede realizar el ciclo.
| Entrada: |
216 125 0 0 |
| Desarrollo: |
x f f' f'' 125.000 6.166; -47.972, -0.451, -0.000 4.975; -0.301, -0.265, -0.010 5.000; 0.006, -0.251, -0.013 5.000; 0.000, -0.251, -0.013 5.000; 0.000, -0.251, -0.013 n= 5 m= ln(216)/ln(5+1)= 3 c= (5^3 -1)/(5 -1)= 31 s= 216(5+1) –5^(3+1)= 1296 –625= 671 |
| Salida: | 31 671 |
Podemos ver como la cantidad de operaciones es mucho menor que con el método de bisección (5 contra 32).
Las principales desventajas del método de Newton es que necesitamos obtener la derivada de la ecuación manualmente, además de que si el valor inicial está lejos de la raíz puede no converger.
Si no queremos encontrar las derivadas, pero queremos algún método rápido, podemos utilizar secantes en lugar de pendientes (método de la secante), que aunque no es tan eficiente como Newton, sigue siendo más rápido que Bisección. El método de la secante presenta el mismo problema de multiplicidad que Newton.
Si queremos encontrar todas raíces de un polinomio, podemos utilizar la regla de Rufino (división sintética) para reducir el grado del polinomio cada que encontramos una raíz, y utilizar un arreglo para guardar los coeficientes del polinomio. Dos métodos que utilizan esto son los de Horner y Müller, lo cuales están basados en los métodos de Newton y de la Secante, respectivamente. La principal ventaja del método de Müller es que puede encontrar también las raíces complejas.

| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 11-Jun-2006 | 1.178 | 0.010 | 0.690 | 29.890 | 324 |
| C | 11-Jun-2006 | 1.148 | 400 | |||
| Pascal | 11-Jun-2006 | 0.551 | 324 | |||
| C | 11-Jun-2006 | 0.357 | 400 | |||
Valladolid:
 Introducción
Introducción
