Existen diversos temas que dentro de los concursos de programación no son tan comunes, como lo puede ser análisis numérico, o que son técnicas que se emplean dentro de otras secciones, como las estructuras de datos, los algoritmos ávidos, o divide y vencerás. En este capítulo se presenta una breve descripción de los fundamentos básicos de cada uno de estos, para que el lector pueda familiarizarse con ellos.

El análisis numérico es el estudio de algoritmos para resolver problemas de matemáticas continuas, siendo los principales temas de interés la solución de problemas con números reales y complejos, problemas de cálculo, ecuaciones diferenciales y ecuaciones lineales, y otros problemas matemáticos que surgen principalmente del campo de la física y la ingeniería.

Una de las principales ventajas del análisis numérico es que puede encontrar soluciones a problemas que no poseen una forma cerrada (esto es, no es posible encontrar una ecuación despejada que nos de el resultado), además del estudio que dedica a la forma en que se deben manejar los errores de redondeo. Por ejemplo, si queremos encontrar la siguiente integral 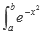, no existe forma de hacerlo de forma directa, pero mediante métodos numéricos podemos encontrar aproximaciones con la cantidad de dígitos que requiramos.

Dentro del análisis numérico se puede clasificar a los problemas en dos categorías: los que pueden ser resueltos de manera exacta por un algoritmo (como en la sección 11.3) a los cuales se le llama métodos directos, y los que a través de aproximaciones sucesiva convergen a una solución (como en la sección 11.2). A estos generalmente se les conoce como métodos iterativos.

En la computadora no podemos trabajar con números reales, ya que sólo poseemos una cantidad finita de dígitos. Para poder utilizar números no enteros, se utilizan números racionales. Cambiar un número real a uno fraccionario, introduce errores, y estos errores se irán propagando a través de los cálculos. A los errores que se producen por la diferencia entre el valor real y el fraccionario se les conoce como errores de redondeo, independientemente de si el valor es redondeado o truncado.

Además de que los números sólo pueden tener cierta precisión dada por la arquitectura de la computadora, también poseen un rango. Cualquier número que este fuera de ese rango tampoco puede ser representado. Los números que son muy grandes para ser representados producen un error de desbordamiento (overflow), mientras que los que son muy pequeños producen uno de subflujo (underflow).

Existen dos formas en que podemos medir un error de aproximación. Si el valor real lo expresamos como real, y a la aproximación como aprox, tenemos que el error absoluto está dado por |real –aprox|, y el error relativo es 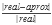. El error absoluto es útil para comparar dos números flotantes (como en los algoritmos geométricos), mientras que el relativo generalmente se utiliza para saber cuando terminar un método iterativo.

Una vez que se generó un error, éste tenderá a mantenerse en los cálculos subsecuentes. Un algoritmo se dice que en numéricamente estable si una vez que ocurre algún error, este no crece demasiado durante los cálculos; en caso contrario se llama inestable. Generalmente un algoritmo estable tiene un error lineal en los cálculos (el error crece a través de una constante), mientras que uno inestable tiene un error exponencial. La rapidez con la que la aproximación tiende al valor real se le conoce como rapidez de convergencia.